Article contents
The remaining cases of the Kramer–Tunnell conjecture
Published online by Cambridge University Press: 29 July 2016
Abstract
For an elliptic curve 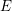 $E$ over a local field
$E$ over a local field 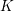 $K$ and a separable quadratic extension of
$K$ and a separable quadratic extension of 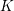 $K$ , motivated by connections to the Birch and Swinnerton-Dyer conjecture, Kramer and Tunnell have conjectured a formula for computing the local root number of the base change of
$K$ , motivated by connections to the Birch and Swinnerton-Dyer conjecture, Kramer and Tunnell have conjectured a formula for computing the local root number of the base change of 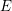 $E$ to the quadratic extension in terms of a certain norm index. The formula is known in all cases except some where
$E$ to the quadratic extension in terms of a certain norm index. The formula is known in all cases except some where 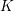 $K$ is of characteristic
$K$ is of characteristic 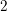 $2$ , and we complete its proof by reducing the positive characteristic case to characteristic
$2$ , and we complete its proof by reducing the positive characteristic case to characteristic 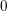 $0$ . For this reduction, we exploit the principle that local fields of characteristic
$0$ . For this reduction, we exploit the principle that local fields of characteristic 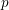 $p$ can be approximated by finite extensions of
$p$ can be approximated by finite extensions of 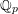 $\mathbb{Q}_{p}$ : we find an elliptic curve
$\mathbb{Q}_{p}$ : we find an elliptic curve 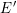 $E^{\prime }$ defined over a
$E^{\prime }$ defined over a 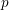 $p$ -adic field such that all the terms in the Kramer–Tunnell formula for
$p$ -adic field such that all the terms in the Kramer–Tunnell formula for 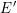 $E^{\prime }$ are equal to those for
$E^{\prime }$ are equal to those for 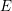 $E$ .
$E$ .
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Authors 2016
References
- 1
- Cited by

