Published online by Cambridge University Press: 01 May 2008
We use Hodge theoretic methods to study homotopy types of complex projective manifolds with arbitrary fundamental groups. The main tool we use is the schematization functor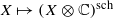 , introduced by the third author as a substitute for the rationalization functor in homotopy theory in the case of non-simply connected spaces. Our main result is the construction of a Hodge decomposition on
, introduced by the third author as a substitute for the rationalization functor in homotopy theory in the case of non-simply connected spaces. Our main result is the construction of a Hodge decomposition on 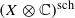 . This Hodge decomposition is encoded in an action of the discrete group
. This Hodge decomposition is encoded in an action of the discrete group 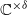 on the object
on the object 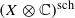 and is shown to recover the usual Hodge decomposition on cohomology, the Hodge filtration on the pro-algebraic fundamental group, and, in the simply connected case, the Hodge decomposition on the complexified homotopy groups. We show that our Hodge decomposition satisfies a purity property with respect to a weight filtration, generalizing the fact that the higher homotopy groups of a simply connected projective manifold have natural mixed Hodge structures. As applications we construct new examples of homotopy types which are not realizable as complex projective manifolds and we prove a formality theorem for the schematization of a complex projective manifold.
and is shown to recover the usual Hodge decomposition on cohomology, the Hodge filtration on the pro-algebraic fundamental group, and, in the simply connected case, the Hodge decomposition on the complexified homotopy groups. We show that our Hodge decomposition satisfies a purity property with respect to a weight filtration, generalizing the fact that the higher homotopy groups of a simply connected projective manifold have natural mixed Hodge structures. As applications we construct new examples of homotopy types which are not realizable as complex projective manifolds and we prove a formality theorem for the schematization of a complex projective manifold.
The first author was partially supported by NSF Career Award DMS-9875383 and an A. P. Sloan research fellowship. The second author was Partially supported by NSF Grants DMS-0099715 and DMS-0403884 and an A. P. Sloan research fellowship.