Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lorscheid, Oliver
2012.
Algebraic groups over the field with one element.
Mathematische Zeitschrift,
Vol. 271,
Issue. 1-2,
p.
117.
Lescot, Paul
2012.
Absolute algebra III—The saturated spectrum.
Journal of Pure and Applied Algebra,
Vol. 216,
Issue. 5,
p.
1004.
Szczesny, Matt
2012.
On the Hall algebra of coherent sheaves on P1 over F1.
Journal of Pure and Applied Algebra,
Vol. 216,
Issue. 3,
p.
662.
Banerjee, Abhishek
2012.
Derived schemes and the field with one element.
Journal de Mathématiques Pures et Appliquées,
Vol. 97,
Issue. 3,
p.
189.
Lorscheid, Oliver
2012.
The geometry of blueprints.
Advances in Mathematics,
Vol. 229,
Issue. 3,
p.
1804.
Chu, Chenghao
Lorscheid, Oliver
and
Santhanam, Rekha
2012.
Sheaves and K-theory for F1-schemes.
Advances in Mathematics,
Vol. 229,
Issue. 4,
p.
2239.
Rohrer, Fred
2013.
The geometry of toric schemes.
Journal of Pure and Applied Algebra,
Vol. 217,
Issue. 4,
p.
700.
Kurokawa, Nobushige
and
Ochiai, Hiroyuki
2013.
Dualities for absolute zeta functions and multiple gamma functions.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 89,
Issue. 7,
DEITMAR, ANTON
2013.
CONGRUENCE SCHEMES.
International Journal of Mathematics,
Vol. 24,
Issue. 02,
p.
1350009.
Pirashvili, Ilia
2013.
On the spectrum of monoids and semilattices.
Journal of Pure and Applied Algebra,
Vol. 217,
Issue. 5,
p.
901.
Connes, Alain
and
Consani, Caterina
2014.
The Arithmetic Site.
Comptes Rendus. Mathématique,
Vol. 352,
Issue. 12,
p.
971.
Connes, Alain
and
Consani, Caterina
2015.
Projective geometry in characteristic one and the epicyclic category.
Nagoya Mathematical Journal,
Vol. 217,
Issue. ,
p.
95.
Lo, Catharine Wing Kwan
and
Marcolli, Matilde
2015.
𝔽ζ-geometry, Tate motives, and the Habiro ring.
International Journal of Number Theory,
Vol. 11,
Issue. 02,
p.
311.
Connes, Alain
and
Consani, Caterina
2015.
Projective geometry in characteristic one and the epicyclic category.
Nagoya Mathematical Journal,
Vol. 217,
Issue. ,
p.
95.
Connes, Alain
and
Consani, Caterina
2016.
Absolute algebra and Segal's Γ-rings.
Journal of Number Theory,
Vol. 162,
Issue. ,
p.
518.
Manin, Yu I
2016.
Local zeta factors and geometries under SpecZ.
Izvestiya: Mathematics,
Vol. 80,
Issue. 4,
p.
751.
Connes, Alain
and
Consani, Caterina
2016.
Geometry of the arithmetic site.
Advances in Mathematics,
Vol. 291,
Issue. ,
p.
274.
Giansiracusa, Jeffrey
and
Giansiracusa, Noah
2016.
Equations of tropical varieties.
Duke Mathematical Journal,
Vol. 165,
Issue. 18,
Lagarias, Jeffrey C.
2016.
A family of measures on symmetric groups and the field with one element.
Journal of Number Theory,
Vol. 161,
Issue. ,
p.
311.
Connes, Alain
2016.
Open Problems in Mathematics.
p.
225.
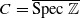 over 𝔽1, whose corresponding zeta function is the complete Riemann zeta function. We show that such a counting function exists as a distribution, is positive on (1,∞) and takes the value −∞ at q=1 as expected from the infinite genus of C. Then, we develop a theory of functorial 𝔽1-schemes which reconciles the previous attempts by Soulé and Deitmar. Our construction fits with the geometry of monoids of Kato, is no longer limited to toric varieties and it covers the case of schemes associated with Chevalley groups. Finally we show, using the monoid of adèle classes over an arbitrary global field, how to apply our functorial theory of
over 𝔽1, whose corresponding zeta function is the complete Riemann zeta function. We show that such a counting function exists as a distribution, is positive on (1,∞) and takes the value −∞ at q=1 as expected from the infinite genus of C. Then, we develop a theory of functorial 𝔽1-schemes which reconciles the previous attempts by Soulé and Deitmar. Our construction fits with the geometry of monoids of Kato, is no longer limited to toric varieties and it covers the case of schemes associated with Chevalley groups. Finally we show, using the monoid of adèle classes over an arbitrary global field, how to apply our functorial theory of 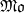 -schemes to interpret conceptually the spectral realization of zeros of L-functions.
-schemes to interpret conceptually the spectral realization of zeros of L-functions.
