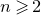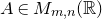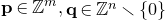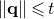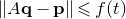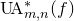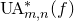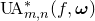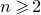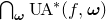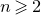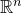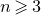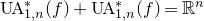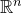1. Introduction
1.1 Background and history
In 1926, Khintchine [Reference KhintchineKhi26] introduced the property of the singularity of vectors, which was later extended to systems of linear forms by Jarník [Reference JarníkJar59]. A matrix
![]() $A \in M_{m,n}(\mathbb{R})$
(viewed as a system of m linear forms in n variables) is singular (notation:
$A \in M_{m,n}(\mathbb{R})$
(viewed as a system of m linear forms in n variables) is singular (notation:
![]() $A\in\operatorname{Sing}_{m,n}$
) if for any
$A\in\operatorname{Sing}_{m,n}$
) if for any
![]() $\varepsilon>0$
there is
$\varepsilon>0$
there is
![]() $t_0>0$
such that for all
$t_0>0$
such that for all
![]() $t \geqslant t_0$
there exist
$t \geqslant t_0$
there exist
![]() $\mathbf{q} \in \mathbb{Z}^n \smallsetminus \{0\}$
and
$\mathbf{q} \in \mathbb{Z}^n \smallsetminus \{0\}$
and
![]() $\mathbf{p} \in \mathbb{Z}^m$
such that
$\mathbf{p} \in \mathbb{Z}^m$
such that
Here
![]() $M_{m,n}(\mathbb{R})$
is the collection of
$M_{m,n}(\mathbb{R})$
is the collection of
![]() $m\times n$
real matrices, and
$m\times n$
real matrices, and
![]() $\|\cdot \|$
stands for the supremum norm on
$\|\cdot \|$
stands for the supremum norm on
![]() $\mathbb{R}^m$
and
$\mathbb{R}^m$
and
![]() $\mathbb{R}^n$
, although the choice of the norm will be immaterial for this work.
$\mathbb{R}^n$
, although the choice of the norm will be immaterial for this work.
Note that (1.1) always has non-trivial integer solutions if
![]() $\varepsilon = 1$
(Dirichlet’s Theorem). Khintchine, and then Jarník with greater generality, showed that while, for
$\varepsilon = 1$
(Dirichlet’s Theorem). Khintchine, and then Jarník with greater generality, showed that while, for
![]() $m=n=1$
, the only singular numbers are rationals, for
$m=n=1$
, the only singular numbers are rationals, for
![]() $\max(m,n) > 1$
there exist uncountably many singular matrices which are totally irrational, that is, not contained in any rational affine subspace of
$\max(m,n) > 1$
there exist uncountably many singular matrices which are totally irrational, that is, not contained in any rational affine subspace of
![]() $M_{m,n}(\mathbb{R})$
. We will denote by
$M_{m,n}(\mathbb{R})$
. We will denote by
![]() $\operatorname{Sing}^*_{m,n}$
the set of totally irrational singular
$\operatorname{Sing}^*_{m,n}$
the set of totally irrational singular
![]() $m\times n$
matrices. Since the work of Khintchine, a large body of work in Diophantine approximation has been devoted to the understanding of
$m\times n$
matrices. Since the work of Khintchine, a large body of work in Diophantine approximation has been devoted to the understanding of
![]() $\operatorname{Sing}^*_{m,n}$
and related sets. See [Reference MoshchevitinMos10] for a detailed survey and an extensive bibliography, and [Reference Kadyrov, Kleinbock, Lindenstrauss and MargulisKKLM17, Reference Das, Fishman, Simmons and UrbańskiDFSU24, Reference Bugeaud, Cheung and ChevalierBCC19] for the computation of the Hausdorff dimension of
$\operatorname{Sing}^*_{m,n}$
and related sets. See [Reference MoshchevitinMos10] for a detailed survey and an extensive bibliography, and [Reference Kadyrov, Kleinbock, Lindenstrauss and MargulisKKLM17, Reference Das, Fishman, Simmons and UrbańskiDFSU24, Reference Bugeaud, Cheung and ChevalierBCC19] for the computation of the Hausdorff dimension of
![]() $\operatorname{Sing}_{m,n}$
and for a discussion of related work.
$\operatorname{Sing}_{m,n}$
and for a discussion of related work.
A natural way to generalize (1.1) is to replace
![]() ${\varepsilon}/{t^{n/m}}$
in the right-hand side by an arbitrary approximating function.
${\varepsilon}/{t^{n/m}}$
in the right-hand side by an arbitrary approximating function.
Definition 1.1. Given a function
![]() $f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
, we say that
$f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
, we say that
![]() $A\in M_{m,n}(\mathbb{R})$
is uniformly f- approximable
Footnote
1
, or f-uniform for brevity, if for every sufficiently large
$A\in M_{m,n}(\mathbb{R})$
is uniformly f- approximable
Footnote
1
, or f-uniform for brevity, if for every sufficiently large
![]() $t>0$
one can find
$t>0$
one can find
![]() $\textbf{q} \in \mathbb{Z}^n\smallsetminus\{0\}$
and
$\textbf{q} \in \mathbb{Z}^n\smallsetminus\{0\}$
and
![]() $\textbf{p} \in \mathbb{Z}^m$
with
$\textbf{p} \in \mathbb{Z}^m$
with
Denote by
![]() $\operatorname{UA}_{m,n}(f)$
the set of f-uniform
$\operatorname{UA}_{m,n}(f)$
the set of f-uniform
![]() $m\times n$
matrices, and by
$m\times n$
matrices, and by
![]() $\operatorname{UA}^*_{m,n}(f)$
the set of totally irrational
$\operatorname{UA}^*_{m,n}(f)$
the set of totally irrational
![]() $A\in \operatorname{UA}_{m,n}(f)$
.
$A\in \operatorname{UA}_{m,n}(f)$
.
We remark that, in general, the field of uniform Diophantine approximation deals with the solvability of systems of type (1.1) or (1.2) for all large enough values of t, as opposed to the (much better understood) theory of asymptotic approximation. There one can define the sets
![]() $\mathcal{A}_{m,n}(f)$
of f-approximable
$\mathcal{A}_{m,n}(f)$
of f-approximable
![]() $m\times n$
matrices, where those systems are required to have integer solutions for an unbounded set of
$m\times n$
matrices, where those systems are required to have integer solutions for an unbounded set of
![]() $t>0$
.
$t>0$
.
Dirichlet’s Theorem asserts that
![]() $ \operatorname{UA}_{m,n}(\phi_{n/m}) = M_{m,n}(\mathbb{R})$
, where we use the notation
$ \operatorname{UA}_{m,n}(\phi_{n/m}) = M_{m,n}(\mathbb{R})$
, where we use the notation
![]() $\phi_a(t) {\, \stackrel{\mathrm{def}}{=}\, } t^{-a}$
. Also one clearly has
$\phi_a(t) {\, \stackrel{\mathrm{def}}{=}\, } t^{-a}$
. Also one clearly has
and, more generally,
![]() $\operatorname{UA}_{m,n}(f)\subset \operatorname{Sing}_{m,n}$
as long as f satisfies
$\operatorname{UA}_{m,n}(f)\subset \operatorname{Sing}_{m,n}$
as long as f satisfies
It is well known (see [Reference CasselsCas57, Chapter V, §7]) that the set of singular matrices is a nullset in
![]() $M_{m,n}(\mathbb{R})$
, and hence so is the set of f-uniform matrices for f satisfying (1.3). It is also clear that matrices A such that
$M_{m,n}(\mathbb{R})$
, and hence so is the set of f-uniform matrices for f satisfying (1.3). It is also clear that matrices A such that
![]() $ A\mathbf{q} = \mathbf{p}$
for some
$ A\mathbf{q} = \mathbf{p}$
for some
![]() $\mathbf{q} \in \mathbb{Z}^n \smallsetminus \{0\}$
and
$\mathbf{q} \in \mathbb{Z}^n \smallsetminus \{0\}$
and
![]() $\mathbf{p} \in \mathbb{Z}^m$
are in
$\mathbf{p} \in \mathbb{Z}^m$
are in
![]() $\operatorname{UA}_{m,n}(f)$
for any f. On the other hand we have the following theorem.
$\operatorname{UA}_{m,n}(f)$
for any f. On the other hand we have the following theorem.
Theorem 1.2. (Jarník [Reference JarníkJar59]). Let
![]() $m,n\in \mathbb{N}$
.
$m,n\in \mathbb{N}$
.
-
(a) If
 $n > 1$
, then for any non-increasing
$n > 1$
, then for any non-increasing
 $f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
the set of totally irrational f-uniform
$f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
the set of totally irrational f-uniform
 $m \times n$
matrices is uncountable and dense.
$m \times n$
matrices is uncountable and dense. -
(b) If, in addition, one assumes that
(1.4)then for any \begin{equation}{\lim_{t\to\infty}tf(t) = \infty,}\end{equation}
\begin{equation}{\lim_{t\to\infty}tf(t) = \infty,}\end{equation}
 $m>1$
the set of totally irrational f-uniform
$m>1$
the set of totally irrational f-uniform
 $m \times 1$
matrices (column vectors) is uncountable and dense.
$m \times 1$
matrices (column vectors) is uncountable and dense.
Remark 1.3. The above theorem is often stated in a simplified form by introducing the notion of the uniform Diophantine exponent
![]() $\hat \omega(A)$
, which is the supremum of a such that A is
$\hat \omega(A)$
, which is the supremum of a such that A is
![]() $\phi_a$
-uniform. In other words,
$\phi_a$
-uniform. In other words,

Then Theorem 1.2 asserts that there exist uncountably many totally irrational
![]() $m\times n$
matrices A with
$m\times n$
matrices A with
![]() $\hat \omega(A) = \infty$
whenever
$\hat \omega(A) = \infty$
whenever
![]() $n>1$
, and uncountably many totally irrational
$n>1$
, and uncountably many totally irrational
![]() $m\times 1$
matrices (column vectors)
$m\times 1$
matrices (column vectors)
![]() $\mathbf{x}$
with
$\mathbf{x}$
with
![]() $\hat \omega(\mathbf{x}) = 1$
as long as
$\hat \omega(\mathbf{x}) = 1$
as long as
![]() $m>1$
.
$m>1$
.
Note that in the column vector case the extra condition (1.4) cannot be removed: indeed, if
![]() $\mathbf{x}$
is such that
$\mathbf{x}$
is such that
![]() $\hat \omega(\mathbf{x}) > 1$
, then one has
$\hat \omega(\mathbf{x}) > 1$
, then one has
![]() $\hat \omega(x_i) > 1$
for every component
$\hat \omega(x_i) > 1$
for every component
![]() $x_i$
of
$x_i$
of
![]() $\mathbf{x}$
, which necessarily implies that
$\mathbf{x}$
, which necessarily implies that
![]() $x_i\in\mathbb{Q}$
for all i. See also the discussion in [Reference Das, Fishman, Simmons and UrbańskiDFSU24, 3.2].
$x_i\in\mathbb{Q}$
for all i. See also the discussion in [Reference Das, Fishman, Simmons and UrbańskiDFSU24, 3.2].
The argument of Khintchine and Jarník has been utilized and extended by many people, including [Reference DaniDan85, Reference WeissWei02, Reference Kleinbock and WadleighKW05]. Most recently, in [Reference Kleinbock, Moshchevitin and WeissKMW21] three of the authors of the present paper showed that, in the case
![]() $m = 1$
, there exist uncountably many f-uniform row vectors on certain submanifolds and fractals. As a special case, they showed that if Y is either a connected analytic submanifold of
$m = 1$
, there exist uncountably many f-uniform row vectors on certain submanifolds and fractals. As a special case, they showed that if Y is either a connected analytic submanifold of
![]() $\mathbb{R}^n$
of dimension at least 2 not contained in a rational affine hyperplane, or a product
$\mathbb{R}^n$
of dimension at least 2 not contained in a rational affine hyperplane, or a product
![]() $\mathcal{C}\times \cdots \times \mathcal{C}$
of
$\mathcal{C}\times \cdots \times \mathcal{C}$
of
![]() $n \geqslant 2$
copies of the middle-third Cantor set
$n \geqslant 2$
copies of the middle-third Cantor set
![]() $\mathcal{C}$
, then Y contains uncountably many f-uniform vectors for any approximating function f.
$\mathcal{C}$
, then Y contains uncountably many f-uniform vectors for any approximating function f.
1.2 Diophantine systems
The goal of this paper is to strengthen the aforementioned results, namely to provide conditions on countably many maps
![]() $\{\varphi_k : k\in\mathbb{N}\}$
from some metric space Y to
$\{\varphi_k : k\in\mathbb{N}\}$
from some metric space Y to
![]() $M_{m_k,n_k}(\mathbb{R})$
under which there is an uncountable and dense set of
$M_{m_k,n_k}(\mathbb{R})$
under which there is an uncountable and dense set of
![]() $y\in Y$
for which
$y\in Y$
for which
![]() $\varphi_k(y)$
is f-uniform for every k. All this will follow from an abstract result (Theorem 1.5) which will generalize many constructions of singular/uniform objects existing in the literature. The proof of Theorem 1.5 once again utilizes the original strategy introduced by Khintchine.
$\varphi_k(y)$
is f-uniform for every k. All this will follow from an abstract result (Theorem 1.5) which will generalize many constructions of singular/uniform objects existing in the literature. The proof of Theorem 1.5 once again utilizes the original strategy introduced by Khintchine.
In order to state our construction in full generality we introduce the notion of a Diophantine system, which is a triple
![]() $\mathcal{X} = ( X, \mathcal{D}, \mathcal{H})$
, where:
$\mathcal{X} = ( X, \mathcal{D}, \mathcal{H})$
, where:
-
– X is a topological space;
-
–
 $\mathcal{D}= \{d_s : s\in \mathcal{I}\}$
is a sequence of continuous functions on X taking nonnegative values (generalized distance functions); and
$\mathcal{D}= \{d_s : s\in \mathcal{I}\}$
is a sequence of continuous functions on X taking nonnegative values (generalized distance functions); and -
–
 $\mathcal{H}= \{h_s: s\in \mathcal{I}\}$
is a sequence of positive real numbers; we will say that
$\mathcal{H}= \{h_s: s\in \mathcal{I}\}$
is a sequence of positive real numbers; we will say that
 $h_s$
is the height associated with
$h_s$
is the height associated with
 $d_s$
.
$d_s$
.
Here
![]() $\mathcal{I}$
is a fixed countable setFootnote
2
of indices. This generalizes the definition of a Diophantine space originally introduced in [Reference Fishman, Simmons and UrbańskiFSU14]; namely, by a Diophantine space one means a triple
$\mathcal{I}$
is a fixed countable setFootnote
2
of indices. This generalizes the definition of a Diophantine space originally introduced in [Reference Fishman, Simmons and UrbańskiFSU14]; namely, by a Diophantine space one means a triple
![]() $(X, \mathcal{R}, H)$
, where X is a complete metric space,
$(X, \mathcal{R}, H)$
, where X is a complete metric space,
![]() $\mathcal{R}$
is a countable dense subset of X, and
$\mathcal{R}$
is a countable dense subset of X, and
![]() $H : \mathcal{R} \to (0, \infty)$
gives the heights of points in
$H : \mathcal{R} \to (0, \infty)$
gives the heights of points in
![]() $\mathcal{R}$
. To view it as a Diophantine system as in our definition one can simply enumerate the elements of
$\mathcal{R}$
. To view it as a Diophantine system as in our definition one can simply enumerate the elements of
![]() $\mathcal{R} = \{r_s: s\in \mathcal{I}\}$
and let
$\mathcal{R} = \{r_s: s\in \mathcal{I}\}$
and let
![]() $d_s(x) {\, \stackrel{\mathrm{def}}{=}\, } \operatorname{dist}(x,r_s)$
and
$d_s(x) {\, \stackrel{\mathrm{def}}{=}\, } \operatorname{dist}(x,r_s)$
and
![]() $h_s {\, \stackrel{\mathrm{def}}{=}\, } H(r_s)$
. Similarly one can treat a more general situation when
$h_s {\, \stackrel{\mathrm{def}}{=}\, } H(r_s)$
. Similarly one can treat a more general situation when
![]() $\mathcal{R}$
is a countable collection of closed subsets of X (resonant sets), which in our notation are simply the zero sets of the generalized distance functions
$\mathcal{R}$
is a countable collection of closed subsets of X (resonant sets), which in our notation are simply the zero sets of the generalized distance functions
![]() $d_s$
. Our setup, however, makes it possible to define the distance from each individual set in a different way, as well as to count the same set several (perhaps infinitely many) times.
$d_s$
. Our setup, however, makes it possible to define the distance from each individual set in a different way, as well as to count the same set several (perhaps infinitely many) times.
Now suppose we are given a Diophantine system
![]() $\mathcal{X} = ( X, \mathcal{D}, \mathcal{H})$
. Then we can introduce the notion of f-uniform points for any function
$\mathcal{X} = ( X, \mathcal{D}, \mathcal{H})$
. Then we can introduce the notion of f-uniform points for any function
![]() $f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
(the approximating function).
$f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
(the approximating function).
Definition 1.4 A point
![]() $x\in X$
is
$x\in X$
is
![]() $(\mathcal{X},f)$
-uniform if for every sufficiently large t one can find
$(\mathcal{X},f)$
-uniform if for every sufficiently large t one can find
![]() $s\in\mathcal{I}$
such that
$s\in\mathcal{I}$
such that
We will denote by
![]() $\operatorname{UA}_{\mathcal{X}}(f)$
the set of
$\operatorname{UA}_{\mathcal{X}}(f)$
the set of
![]() $(\mathcal{X},f)$
-uniform points of X.
$(\mathcal{X},f)$
-uniform points of X.
As the reader can easily check, the following choices define a Diophantine system, which we refer to as the standard Diophantine system
![]() $\mathcal{X}_{m,n}$
:
$\mathcal{X}_{m,n}$
:
It is clear that a matrix is
![]() $({\mathcal{X}_{m,n}}, f)$
-uniform if and only if it is f-uniform in the sense of Definition 1.1.
$({\mathcal{X}_{m,n}}, f)$
-uniform if and only if it is f-uniform in the sense of Definition 1.1.
Trivially, every point in the union of resonant sets
![]() $d_s^{-1}(\{0\})$
is
$d_s^{-1}(\{0\})$
is
![]() $(\mathcal{X},f)$
-uniform for any choice of
$(\mathcal{X},f)$
-uniform for any choice of
![]() $\mathcal{H}$
and f. In the next section we will state our main theorem, which provides a set of conditions guaranteeing the existence of uncountably many non-trivial
$\mathcal{H}$
and f. In the next section we will state our main theorem, which provides a set of conditions guaranteeing the existence of uncountably many non-trivial
![]() $(\mathcal{X},f)$
-uniform points. More generally, it involves an auxiliary metric space Y and countably many maps from Y to possibly different metric spaces
$(\mathcal{X},f)$
-uniform points. More generally, it involves an auxiliary metric space Y and countably many maps from Y to possibly different metric spaces
![]() $X_i$
, each endowed with its own Diophantine system.
$X_i$
, each endowed with its own Diophantine system.
1.3 The main result
To state our main abstract theorem, it will be convenient to introduce some more terminology. Let Y be a metric space and let
![]() $\mathcal{L}$
,
$\mathcal{L}$
,
![]() $\mathcal{R}$
be two collections of proper closed subsets of Y. We say that
$\mathcal{R}$
be two collections of proper closed subsets of Y. We say that
![]() $\mathcal{L}$
is totally dense relative to
$\mathcal{L}$
is totally dense relative to
![]() $\mathcal{R}$
if
$\mathcal{R}$
if
and
We will say that
![]() $\mathcal{L}$
is totally dense if it is totally dense relative to the collection of all closed nowhere dense subsets of Y. In this case (1.8) is equivalent to
$\mathcal{L}$
is totally dense if it is totally dense relative to the collection of all closed nowhere dense subsets of Y. In this case (1.8) is equivalent to
 \begin{equation}{\begin{aligned} \forall\text{ open } W \subset Y \text{ and } \forall\,L\in \mathcal{L} \text{ such that }L \cap W \neq, \varnothing \\ \text{the closure of } \bigcup_{L'\in \mathcal{L}\,:\,L'\cap L \cap W \ne \varnothing}L' \text{ has a non-empty interior}.\end{aligned}}\end{equation}
\begin{equation}{\begin{aligned} \forall\text{ open } W \subset Y \text{ and } \forall\,L\in \mathcal{L} \text{ such that }L \cap W \neq, \varnothing \\ \text{the closure of } \bigcup_{L'\in \mathcal{L}\,:\,L'\cap L \cap W \ne \varnothing}L' \text{ has a non-empty interior}.\end{aligned}}\end{equation}
For example, for any
![]() $1\leqslant d < n$
the collection
$1\leqslant d < n$
the collection
![]() $\mathcal{L}$
of d-dimensional rational affine subspaces of
$\mathcal{L}$
of d-dimensional rational affine subspaces of
![]() $Y = \mathbb{R}^n$
is totally dense, with the union in (1.9) being dense in
$Y = \mathbb{R}^n$
is totally dense, with the union in (1.9) being dense in
![]() $\mathbb{R}^n$
. More examples will be described later in the paper. On the other hand, the collection of straight lines in
$\mathbb{R}^n$
. More examples will be described later in the paper. On the other hand, the collection of straight lines in
![]() $\mathbb{R}^3$
that are parallel to one of the coordinate axes satisfies properties (1.7) and (1.8) with
$\mathbb{R}^3$
that are parallel to one of the coordinate axes satisfies properties (1.7) and (1.8) with
![]() $\mathcal{R} = $
all planes in
$\mathcal{R} = $
all planes in
![]() $\mathbb{R}^3$
, but not (1.9).
$\mathbb{R}^3$
, but not (1.9).
Here is another definition which will be important for us throughout the paper. Let us say that
![]() $\mathcal{L}$
respects a subset R of Y if whenever
$\mathcal{L}$
respects a subset R of Y if whenever
![]() $L\in \mathcal{L}$
is such that
$L\in \mathcal{L}$
is such that
![]() $L\cap R$
has non-empty interior in L (in the topology induced from Y), it follows that
$L\cap R$
has non-empty interior in L (in the topology induced from Y), it follows that
![]() $L\subset R$
. In other words, elements L of
$L\subset R$
. In other words, elements L of
![]() $\mathcal{L}$
are not allowed to behave disrespectfully by intersecting R in an open set and then wandering off. We will say that
$\mathcal{L}$
are not allowed to behave disrespectfully by intersecting R in an open set and then wandering off. We will say that
![]() $\mathcal{L}$
respects
$\mathcal{L}$
respects
![]() $\mathcal{R}$
if it respects every
$\mathcal{R}$
if it respects every
![]() $R\in \mathcal{R}$
. As an example, if each element of
$R\in \mathcal{R}$
. As an example, if each element of
![]() $\mathcal{L}$
is either connected or has no isolated points, it respects any singleton
$\mathcal{L}$
is either connected or has no isolated points, it respects any singleton
![]() $\{y\}\subset Y$
. Another example is given by collections
$\{y\}\subset Y$
. Another example is given by collections
![]() $\mathcal{L}$
and
$\mathcal{L}$
and
![]() $\mathcal{R}$
consisting of analytic submanifolds of
$\mathcal{R}$
consisting of analytic submanifolds of
![]() $\mathbb{R}^n$
(where we equip them with the metric inherited from the ambient space
$\mathbb{R}^n$
(where we equip them with the metric inherited from the ambient space
![]() $\mathbb{R}^n$
) such that every
$\mathbb{R}^n$
) such that every
![]() $L\in \mathcal{L}$
is connected, and every
$L\in \mathcal{L}$
is connected, and every
![]() $R\in \mathcal{R}$
is closed; see Lemma 3.2 for more details.
$R\in \mathcal{R}$
is closed; see Lemma 3.2 for more details.
Our final definition involves a collection
![]() $\mathcal{L}$
of proper closed subsets of Y, a Diophantine system
$\mathcal{L}$
of proper closed subsets of Y, a Diophantine system
![]() $\mathcal{X} = ( X, \mathcal{D}, \mathcal{H})$
, and a map
$\mathcal{X} = ( X, \mathcal{D}, \mathcal{H})$
, and a map
![]() $\varphi: Y\to X$
. Let us say that
$\varphi: Y\to X$
. Let us say that
![]() $\mathcal{L}$
is aligned with
$\mathcal{L}$
is aligned with
![]() $\mathcal{X}$
via
$\mathcal{X}$
via
![]() $\varphi$
if for any
$\varphi$
if for any
![]() $L\in \mathcal{L}$
there exists
$L\in \mathcal{L}$
there exists
![]() $s\in\mathcal{I}$
such that
$s\in\mathcal{I}$
such that
![]() $d_{s}|_{\varphi(L)}\equiv 0$
; in other words, if
$d_{s}|_{\varphi(L)}\equiv 0$
; in other words, if
![]() $\varphi(L)$
is contained in one of the resonant sets
$\varphi(L)$
is contained in one of the resonant sets
![]() $d_s^{-1}(\{0\})$
. In the special case when
$d_s^{-1}(\{0\})$
. In the special case when
![]() $Y = X$
and
$Y = X$
and
![]() $\varphi = \operatorname{Id}$
we will simply say that
$\varphi = \operatorname{Id}$
we will simply say that
![]() $\mathcal{L}$
is aligned with
$\mathcal{L}$
is aligned with
![]() $\mathcal{X}$
. Note that this property is independent both of the choice of the height functions
$\mathcal{X}$
. Note that this property is independent both of the choice of the height functions
![]() $h_s$
and of a reparametrization of generalized distance functions as long as their zero sets are fixed.
$h_s$
and of a reparametrization of generalized distance functions as long as their zero sets are fixed.
Now we are ready to state the main theorem of the paper.
Theorem 1.5. Let Y be a locally compact metric space. For any
![]() $k\in \mathbb{N}$
suppose we are given a Diophantine system
$k\in \mathbb{N}$
suppose we are given a Diophantine system
and a non-increasing function
![]() $f_k: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
, and let
$f_k: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
, and let
![]() $\varphi_k$
be a continuous map from Y to
$\varphi_k$
be a continuous map from Y to
![]() $X_k$
. Let
$X_k$
. Let
![]() $\mathcal{L}$
and
$\mathcal{L}$
and
![]() $\mathcal{R}$
be countable collections of closed subsets of Y such that
$\mathcal{R}$
be countable collections of closed subsets of Y such that
![]() $\mathcal{L}$
is totally dense relative to
$\mathcal{L}$
is totally dense relative to
![]() $\mathcal{R}$
, respects
$\mathcal{R}$
, respects
![]() $\mathcal{R}$
, and is aligned with
$\mathcal{R}$
, and is aligned with
![]() $\mathcal{X}_k$
via
$\mathcal{X}_k$
via
![]() $\varphi_k$
for every
$\varphi_k$
for every
![]() $k\in\mathbb{N}$
. Then:
$k\in\mathbb{N}$
. Then:
-
(a) the set
(1.11)is dense in Y-1pt; and \begin{equation}{\bigcap_{k} \varphi_k^{-1}\big(\operatorname{UA}_{\mathcal{X}_k}(f_k)\big) \smallsetminus \bigcup_{{R\in\mathcal{R}}} R }\end{equation}
\begin{equation}{\bigcap_{k} \varphi_k^{-1}\big(\operatorname{UA}_{\mathcal{X}_k}(f_k)\big) \smallsetminus \bigcup_{{R\in\mathcal{R}}} R }\end{equation}
-
(b) in addition, if every
 $L\in\mathcal{L}$
is either connected or has no isolated points, the set (1.11) is uncountable.
$L\in\mathcal{L}$
is either connected or has no isolated points, the set (1.11) is uncountable.
Remark 1.6. A few comments are in order.
-
(1) In the above statement we are working with an indexed collection
 $\mathcal{X}_k$
, which is shorthand for a function
$\mathcal{X}_k$
, which is shorthand for a function
 $k \mapsto \mathcal{X}_k$
; we do not assume that this function is injective. It might also happen that the underlying set
$k \mapsto \mathcal{X}_k$
; we do not assume that this function is injective. It might also happen that the underlying set
 $X_k$
of
$X_k$
of
 $\mathcal{X}_k = (X_k, \mathcal{D}_k,\mathcal{H}_k)$
arises several times, with distinct generalized distance functions or height functions.
$\mathcal{X}_k = (X_k, \mathcal{D}_k,\mathcal{H}_k)$
arises several times, with distinct generalized distance functions or height functions. -
(2) Neither the approximation functions
 $f_k$
nor the heights
$f_k$
nor the heights
 $\mathcal{H}_k$
appear in the conditions of the theorem. Moreover, the collections
$\mathcal{H}_k$
appear in the conditions of the theorem. Moreover, the collections
 $\mathcal{D}_k$
of generalized distance functions appear only through their zero sets
$\mathcal{D}_k$
of generalized distance functions appear only through their zero sets
 $d_{k,s}^{-1}(\{0\})$
. Thus if the assumptions of the above theorem are satisfied, then they are satisfied for all positive non-increasing functions
$d_{k,s}^{-1}(\{0\})$
. Thus if the assumptions of the above theorem are satisfied, then they are satisfied for all positive non-increasing functions
 $f_k$
, all choices of the heights, and all choices of generalized distance functions as long as their zero sets are fixed.
$f_k$
, all choices of the heights, and all choices of generalized distance functions as long as their zero sets are fixed. -
(3) It is easy to see that Theorem 1.5 holds for finite intersections, that is, when the set of indices k is finite; this follows immediately from the statement of the theorem, taking
 $f_k, \varphi_k, \mathcal{X}_k$
to be the same for all sufficiently large k.
$f_k, \varphi_k, \mathcal{X}_k$
to be the same for all sufficiently large k.
Theorem 1.5 is proved in § 2, and in § 3 we show that it implies a strengthening of Theorem 1.2(a), making it possible to avoid countably many proper analytic submanifolds in
![]() $M_{m,n}(\mathbb{R})$
(see Theorem 3.3). In the remainder of the introduction we present a list of additional applications of Theorem 1.5.
$M_{m,n}(\mathbb{R})$
(see Theorem 3.3). In the remainder of the introduction we present a list of additional applications of Theorem 1.5.
1.4 Matrices uniformly approximable with different weights
Many results in Diophantine approximation extend to approximation with weights, an approach in which one gives different treatment to different linear forms
![]() $A_i $
(the rows of A), as well as different components of
$A_i $
(the rows of A), as well as different components of
![]() $\textbf{q}$
.
$\textbf{q}$
.
For an
![]() $(m+n)$
-tuple of positive weightsFootnote
3
$(m+n)$
-tuple of positive weightsFootnote
3
![]() $ {\boldsymbol{\omega}} = ({\boldsymbol{\alpha}},{\boldsymbol{\beta}}) \in \mathbb{R}_{>0}^{m+n} $
, where
$ {\boldsymbol{\omega}} = ({\boldsymbol{\alpha}},{\boldsymbol{\beta}}) \in \mathbb{R}_{>0}^{m+n} $
, where
![]() ${\boldsymbol{\alpha}} = (\alpha_1,\dots,\alpha_m)\in\mathbb{R}_{>0}^m$
and
${\boldsymbol{\alpha}} = (\alpha_1,\dots,\alpha_m)\in\mathbb{R}_{>0}^m$
and
![]() ${\boldsymbol{\beta}} = (\beta_1,\dots,\beta_n)\in\mathbb{R}_{>0}^n$
, let us introduce quasi-norms
${\boldsymbol{\beta}} = (\beta_1,\dots,\beta_n)\in\mathbb{R}_{>0}^n$
, let us introduce quasi-norms
on
![]() $\mathbb{R}^m$
and
$\mathbb{R}^m$
and
![]() $\mathbb{R}^n$
respectively. Then, for f as above, one says that
$\mathbb{R}^n$
respectively. Then, for f as above, one says that
![]() $A\in M_{m,n}(\mathbb{R})$
is
$A\in M_{m,n}(\mathbb{R})$
is
![]() $(f, {\boldsymbol{\omega}})$
- uniform, denoted by
$(f, {\boldsymbol{\omega}})$
- uniform, denoted by
![]() $A\in \operatorname{UA}_{m,n}(f, {\boldsymbol{\omega}})$
, if for every sufficiently large t one can find
$A\in \operatorname{UA}_{m,n}(f, {\boldsymbol{\omega}})$
, if for every sufficiently large t one can find
![]() $\textbf{q} \in \mathbb{Z}^n\smallsetminus\{0\}$
and
$\textbf{q} \in \mathbb{Z}^n\smallsetminus\{0\}$
and
![]() $\textbf{p} \in \mathbb{Z}^m$
with
$\textbf{p} \in \mathbb{Z}^m$
with
In other words, we are considering the solvability of the system
 \begin{equation*} \begin{cases} | A_i \textbf{q} - p_i| \leqslant f(t)^{\alpha_i}, & i = 1,\dots,m;\\ |q_j|\leqslant t^{\beta_j},& j = 1,\dots,n.\end{cases}\end{equation*}
\begin{equation*} \begin{cases} | A_i \textbf{q} - p_i| \leqslant f(t)^{\alpha_i}, & i = 1,\dots,m;\\ |q_j|\leqslant t^{\beta_j},& j = 1,\dots,n.\end{cases}\end{equation*}
See [Reference Kleinbock and RaoKR22] for a discussion. Clearly the unweighted case corresponds to the choice
![]() ${\boldsymbol{\omega}} = (1,\dots,1)$
. As in Definition 1.1, let us denote by
${\boldsymbol{\omega}} = (1,\dots,1)$
. As in Definition 1.1, let us denote by
![]() $\operatorname{UA}^*_{m,n}(f, {\boldsymbol{\omega}})$
the set of totally irrational
$\operatorname{UA}^*_{m,n}(f, {\boldsymbol{\omega}})$
the set of totally irrational
![]() $A\in \operatorname{UA}_{m,n}(f, {\boldsymbol{\omega}})$
.
$A\in \operatorname{UA}_{m,n}(f, {\boldsymbol{\omega}})$
.
Clearly for any
![]() $ {\boldsymbol{\omega}} = ({\boldsymbol{\alpha}},{\boldsymbol{\beta}})$
and f as above one has
$ {\boldsymbol{\omega}} = ({\boldsymbol{\alpha}},{\boldsymbol{\beta}})$
and f as above one has
Hence it immediately follows from Theorem 1.2(a) that
![]() $\operatorname{UA}^*_{m,n}(f, {\boldsymbol{\omega}})$
is uncountable and dense. Using Theorem 1.5 one can extend this to matrices which are simultaneously
$\operatorname{UA}^*_{m,n}(f, {\boldsymbol{\omega}})$
is uncountable and dense. Using Theorem 1.5 one can extend this to matrices which are simultaneously
![]() $(f_k, {\boldsymbol{\omega}}_k)$
-uniform for countably many k.
$(f_k, {\boldsymbol{\omega}}_k)$
-uniform for countably many k.
Theorem 1.7. Let
![]() $n \geqslant 2$
and
$n \geqslant 2$
and
![]() $m \in \mathbb{N}$
.
$m \in \mathbb{N}$
.
-
(a) For any sequence
 ${\boldsymbol{\omega}}_1, {\boldsymbol{\omega}}_2, \ldots \in \mathbb{R}_{>0}^{m+n}$
of weight vectors and any sequence
${\boldsymbol{\omega}}_1, {\boldsymbol{\omega}}_2, \ldots \in \mathbb{R}_{>0}^{m+n}$
of weight vectors and any sequence
 $f_1, f_2, \ldots$
of positive non-increasing functions, the intersection
$f_1, f_2, \ldots$
of positive non-increasing functions, the intersection
 $\bigcap_k\operatorname{UA}^*_{m,n}(f_k, {\boldsymbol{\omega}}_k)$
is dense and uncountable.
$\bigcap_k\operatorname{UA}^*_{m,n}(f_k, {\boldsymbol{\omega}}_k)$
is dense and uncountable. -
(b) The intersection
 $\bigcap_{{\boldsymbol{\omega}} \in \mathbb{R}_{>0}^{m+n}}\operatorname{UA}^*_{m,n}(f, {\boldsymbol{\omega}})$
is dense and uncountable for any positive non-increasing f.
$\bigcap_{{\boldsymbol{\omega}} \in \mathbb{R}_{>0}^{m+n}}\operatorname{UA}^*_{m,n}(f, {\boldsymbol{\omega}})$
is dense and uncountable for any positive non-increasing f.
In § 3 we prove an even stronger statement, with extra uniformity in choosing approximating vectors and making it possible to avoid countably many proper analytic submanifolds (see Theorem 3.4).
1.5 Uniform approximation of higher order on submanifolds
In § 4 we show that, in the row vector case (
![]() $m=1$
), vectors satisfying the conclusions of Theorem 1.7 exist on many manifolds and fractals. For example the following theorem, which is a special case of Theorem 4.2, was already proved in [Reference Kleinbock, Moshchevitin and WeissKMW21].
$m=1$
), vectors satisfying the conclusions of Theorem 1.7 exist on many manifolds and fractals. For example the following theorem, which is a special case of Theorem 4.2, was already proved in [Reference Kleinbock, Moshchevitin and WeissKMW21].
Theorem 1.8. Let Y be a connected analytic submanifold of
![]() $\mathbb{R}^n$
of dimension at least 2 that is not contained in a rational affine hyperplane, and let f be any positive non-increasing function. Then the intersection of
$\mathbb{R}^n$
of dimension at least 2 that is not contained in a rational affine hyperplane, and let f be any positive non-increasing function. Then the intersection of
![]() $\operatorname{UA}^*_{1,n}(f)$
with Y is dense and uncountable.
$\operatorname{UA}^*_{1,n}(f)$
with Y is dense and uncountable.
Our proof, based on Theorem 1.5, makes it possible to streamline the argument and derive other related results. In particular, one benefit of our level of abstraction is that we can similarly study uniform approximation of higher order. Let us introduce the following
Definition 1.9. Given a function
![]() $f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
and
$f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
and
![]() $1\leqslant g \leqslant n$
, we say that
$1\leqslant g \leqslant n$
, we say that
![]() $\mathbf{x} \in \mathbb{R}^n$
is f-uniform of order g (notation:
$\mathbf{x} \in \mathbb{R}^n$
is f-uniform of order g (notation:
![]() $\mathbf{x}\in\operatorname{UA}_{1,n}(f; g)$
, or
$\mathbf{x}\in\operatorname{UA}_{1,n}(f; g)$
, or
![]() $\mathbf{x}\in\operatorname{UA}^*_{1,n}(f; g)$
if
$\mathbf{x}\in\operatorname{UA}^*_{1,n}(f; g)$
if
![]() $\mathbf{x}$
is totally irrational) if for every sufficiently large
$\mathbf{x}$
is totally irrational) if for every sufficiently large
![]() $t>0$
one can find linearly independent
$t>0$
one can find linearly independent
![]() $\mathbf{q}_1, \ldots, \mathbf{q}_g$
in
$\mathbf{q}_1, \ldots, \mathbf{q}_g$
in
![]() $\mathbb{Z}^n$
and
$\mathbb{Z}^n$
and
![]() $p_1, \ldots, p_g \in \mathbb{Z}$
such that
$p_1, \ldots, p_g \in \mathbb{Z}$
such that
Note that any rational affine subspace of codimension g is an intersection of g rational affine hyperplanes with linearly independent normal vectors, and hence every point of it is f-uniform of order g for any f. The following generalization of Theorem 1.8 is a special case of Theorem 4.2.
Theorem 1.10.
Let Y be a connected analytic submanifold of
![]() $\mathbb{R}^n$
of dimension
$\mathbb{R}^n$
of dimension
![]() $d\geqslant 2$
not contained in a rational affine hyperplane, let f be any positive non-increasing function, and let
$d\geqslant 2$
not contained in a rational affine hyperplane, let f be any positive non-increasing function, and let
![]() $1\leqslant g \leqslant d-1$
. Then the intersection of Y with
$1\leqslant g \leqslant d-1$
. Then the intersection of Y with
![]() $\operatorname{UA}^*_{1,n}(f; g)$
is dense and uncountable.
$\operatorname{UA}^*_{1,n}(f; g)$
is dense and uncountable.
1.6 Vectors which are k-singular for all k
A vector
![]() $\mathbf{x} \in \mathbb{R}^n$
is called k-singular [Reference Kristensen, Pedersen and WeissKPW16] if for any
$\mathbf{x} \in \mathbb{R}^n$
is called k-singular [Reference Kristensen, Pedersen and WeissKPW16] if for any
![]() $\varepsilon>0$
there is
$\varepsilon>0$
there is
![]() $Q_0>0$
such that for all
$Q_0>0$
such that for all
![]() $Q > Q_0$
there exists a polynomial
$Q > Q_0$
there exists a polynomial
![]() $P \in \mathbb{Z}[X_1, \ldots, X_n]$
such that
$P \in \mathbb{Z}[X_1, \ldots, X_n]$
such that
Here H(P) is the height of P, defined as the maximum of the absolute value of the coefficients of P,
![]() $\deg(P)$
is the total degree of P, and
$\deg(P)$
is the total degree of P, and
Note that when
![]() $k=1$
, k-singularity is the same as the singularity of
$k=1$
, k-singularity is the same as the singularity of
![]() $\mathbf{x}$
considered as a row vector in
$\mathbf{x}$
considered as a row vector in
![]() $M_{1,n}(\mathbb{R})$
, and the existence of singular vectors in certain manifolds and fractals is one of the main results of [Reference Kleinbock, Moshchevitin and WeissKMW21].
$M_{1,n}(\mathbb{R})$
, and the existence of singular vectors in certain manifolds and fractals is one of the main results of [Reference Kleinbock, Moshchevitin and WeissKMW21].
The study of k-singular vectors is related to the approximation of
![]() $\mathbf{x}$
by vectors with algebraic coefficients of degree at most k; see e.g. [Reference YuYu87]. Following [Reference Kristensen, Pedersen and WeissKPW16], let us say that
$\mathbf{x}$
by vectors with algebraic coefficients of degree at most k; see e.g. [Reference YuYu87]. Following [Reference Kristensen, Pedersen and WeissKPW16], let us say that
![]() $\mathbf{x}$
is k-algebraic if there is a nonzero polynomial
$\mathbf{x}$
is k-algebraic if there is a nonzero polynomial
![]() ${P \in \mathbb{Z}[X_1, \ldots,X_n]}$
such that
${P \in \mathbb{Z}[X_1, \ldots,X_n]}$
such that
![]() $P(\mathbf{x})=0$
and
$P(\mathbf{x})=0$
and
![]() $\deg P =k$
, and we say it is algebraic if it is k-algebraic for some k. It is easy to see that a k-algebraic vector is k’-singular for every
$\deg P =k$
, and we say it is algebraic if it is k-algebraic for some k. It is easy to see that a k-algebraic vector is k’-singular for every
![]() $k'\geqslant k$
, and it was shown in [Reference Kristensen, Pedersen and WeissKPW16] that for
$k'\geqslant k$
, and it was shown in [Reference Kristensen, Pedersen and WeissKPW16] that for
![]() $n \geqslant 2$
and for each k there are k-singular vectors which are not k-algebraic. In § 5 we show the following theorem.
$n \geqslant 2$
and for each k there are k-singular vectors which are not k-algebraic. In § 5 we show the following theorem.
Theorem 1.11. If
![]() $n \geqslant 2$
, then there is a dense uncountable set of
$n \geqslant 2$
, then there is a dense uncountable set of
![]() $\mathbf{x} \in \mathbb{R}^n$
such that
$\mathbf{x} \in \mathbb{R}^n$
such that
![]() $\mathbf{x}$
is k-singular for all
$\mathbf{x}$
is k-singular for all
![]() $k \in \mathbb{N}$
, but
$k \in \mathbb{N}$
, but
![]() $\mathbf{x}$
is not algebraic.
$\mathbf{x}$
is not algebraic.
Theorem 1.11 answers a question raised in [Reference Kristensen, Pedersen and WeissKPW16, 2.3] regarding the existence of vectors which are
![]() $(k,\varepsilon)$
-Dirichlet improvable for some fixed
$(k,\varepsilon)$
-Dirichlet improvable for some fixed
![]() $\varepsilon$
, for all positive integers k. Note that we are going to prove a statement much more general than Theorem 1.11; namely, we will discuss vectors that are uniformly
$\varepsilon$
, for all positive integers k. Note that we are going to prove a statement much more general than Theorem 1.11; namely, we will discuss vectors that are uniformly
![]() $f_k$
-approximable of degree k for each k, where
$f_k$
-approximable of degree k for each k, where
![]() $f_k$
is a sequence of arbitrary positive non-increasing functions. Moreover, those vectors will be found in many manifolds and fractals.
$f_k$
is a sequence of arbitrary positive non-increasing functions. Moreover, those vectors will be found in many manifolds and fractals.
1.7
 $\operatorname{Sing}^*_{1,n}+ \operatorname{Sing}^*_{1,n} = \mathbb{R}^n$
and generalizations
$\operatorname{Sing}^*_{1,n}+ \operatorname{Sing}^*_{1,n} = \mathbb{R}^n$
and generalizations
Here we consider the case
![]() $m = 1$
. It is known [Reference Das, Fishman, Simmons and UrbańskiDFSU24] that for rapidly decaying f the sets
$m = 1$
. It is known [Reference Das, Fishman, Simmons and UrbańskiDFSU24] that for rapidly decaying f the sets
![]() $\operatorname{UA}_{1,n}(f)$
have very small Hausdorff dimension. The next theorem shows that when
$\operatorname{UA}_{1,n}(f)$
have very small Hausdorff dimension. The next theorem shows that when
![]() $n\geqslant 3$
the sum of two such sets is the whole space.
$n\geqslant 3$
the sum of two such sets is the whole space.
Theorem 1.12.
If
![]() $n \geqslant 3$
, then for any two non-increasing functions
$n \geqslant 3$
, then for any two non-increasing functions
![]() $f_1,f_2:\mathbb{R}_{>0} \to \mathbb{R}_{>0}$
one has
$f_1,f_2:\mathbb{R}_{>0} \to \mathbb{R}_{>0}$
one has
See Schleischitz [Reference SchleischitzSch22, 3] for related work. We prove this theorem in § 6 and discuss several extensions.
1.8 Improved rates of singularity for column vectors
Recall from Theorem 1.2 that for
![]() $n>1$
, any
$n>1$
, any
![]() $m\in\mathbb{N}$
and any positive non-increasing f one can find an
$m\in\mathbb{N}$
and any positive non-increasing f one can find an
![]() $m\times n$
matrix which is totally irrational and f-uniform. For
$m\times n$
matrix which is totally irrational and f-uniform. For
![]() $n=1$
and
$n=1$
and
![]() $ m>1$
, that is for the case of column vectors, this is no longer the case. Indeed, as was mentioned in Remark 1.3, for all totally irrational
$ m>1$
, that is for the case of column vectors, this is no longer the case. Indeed, as was mentioned in Remark 1.3, for all totally irrational
![]() $\mathbf{x}\in\mathbb{R}^m \cong M_{m,1}(\mathbb{R})$
one has
$\mathbf{x}\in\mathbb{R}^m \cong M_{m,1}(\mathbb{R})$
one has
![]() $\hat\omega(\mathbf{x})\leqslant 1$
, and, according to Theorem 1.2(b), this maximum value is attained on an uncountable dense set. It is natural to inquire about the value of
$\hat\omega(\mathbf{x})\leqslant 1$
, and, according to Theorem 1.2(b), this maximum value is attained on an uncountable dense set. It is natural to inquire about the value of
![]() $\hat \omega$
that vectors in certain fractals and submanifolds may attain. One can approach this question by the standard transference argument as in [Reference CasselsCas57, Chapter∼V, TheoremII] and [Reference JarníkJar38] and show that any column vector
$\hat \omega$
that vectors in certain fractals and submanifolds may attain. One can approach this question by the standard transference argument as in [Reference CasselsCas57, Chapter∼V, TheoremII] and [Reference JarníkJar38] and show that any column vector
![]() $\mathbf{x}\in {\mathbb{R}^n\cong M_{n,1}(\mathbb{R})}$
with
$\mathbf{x}\in {\mathbb{R}^n\cong M_{n,1}(\mathbb{R})}$
with
![]() $\hat\omega(\mathbf{x}^T) = \infty$
satisfies
$\hat\omega(\mathbf{x}^T) = \infty$
satisfies
Therefore an application of Theorem 1.8 coupled with transference will produce, for manifolds Y as in that theorem, a dense uncountable set of
![]() $\mathbf{x}\in Y$
satisfying (1.16).
$\mathbf{x}\in Y$
satisfying (1.16).
It is natural to seek an improvement of the above bound; however, replacing
![]() $1/{({{n}}-1)}$
with 1 on an arbitrary analytic submanifold of
$1/{({{n}}-1)}$
with 1 on an arbitrary analytic submanifold of
![]() $\mathbb{R}^{{n}}$
is an impossible task. Indeed, in [Reference Kleinbock and MoshchevitinKM19] it was shown that certain submanifolds do not contain column vectors
$\mathbb{R}^{{n}}$
is an impossible task. Indeed, in [Reference Kleinbock and MoshchevitinKM19] it was shown that certain submanifolds do not contain column vectors
![]() $\mathbf{x}$
with
$\mathbf{x}$
with
![]() $\hat\omega(\mathbf{x}) = 1$
. Namely, letting
$\hat\omega(\mathbf{x}) = 1$
. Namely, letting
![]() $H_{{n}} \in\big(\frac12,1\big)$
be the unique positive root of the equation
$H_{{n}} \in\big(\frac12,1\big)$
be the unique positive root of the equation
![]() $x + \cdots + x^{{{n}}+1} =1$
, it was proved that any
$x + \cdots + x^{{{n}}+1} =1$
, it was proved that any
![]() $\mathbf{x}$
in the sphere
$\mathbf{x}$
in the sphere
![]() $\{(x_1, \ldots,x_{{n}}): \sum x^2_i =1\} $
satisfies
$\{(x_1, \ldots,x_{{n}}): \sum x^2_i =1\} $
satisfies
![]() $\hat \omega(\mathbf{x}) \leqslant H_{{{n}}-1}$
, and any
$\hat \omega(\mathbf{x}) \leqslant H_{{{n}}-1}$
, and any
![]() $\mathbf{x}$
in the paraboloid
$\mathbf{x}$
in the paraboloid
![]() $\{(x_1, \ldots, x_{{n}}): x_{{n}} = \sum_{i<{{n}}} x_i^2\}$
satisfies
$\{(x_1, \ldots, x_{{n}}): x_{{n}} = \sum_{i<{{n}}} x_i^2\}$
satisfies
![]() $\hat \omega(\mathbf{x}) \leqslant H_{{{n}}}$
. Furthermore, in [Reference Kleinbock, Moshchevitin and WeissKMW21] it was shown that there are d-dimensional affine subspaces
$\hat \omega(\mathbf{x}) \leqslant H_{{{n}}}$
. Furthermore, in [Reference Kleinbock, Moshchevitin and WeissKMW21] it was shown that there are d-dimensional affine subspaces
![]() $L \subset \mathbb{R}^{{n}}$
such that any
$L \subset \mathbb{R}^{{n}}$
such that any
![]() $\mathbf{x} \in L$
satisfies
$\mathbf{x} \in L$
satisfies
![]() $\hat \omega(\mathbf{x})\leqslant (d+1)/(n-d)$
, which is strictly smaller than 1 for
$\hat \omega(\mathbf{x})\leqslant (d+1)/(n-d)$
, which is strictly smaller than 1 for
![]() $d < ({n}-1)/2 $
. In § 7, using uniform approximation of higher order, i.e. Theorem 1.10, together with a transference argument, we are able to improve the bound in (1.16) and prove the following theorem.
$d < ({n}-1)/2 $
. In § 7, using uniform approximation of higher order, i.e. Theorem 1.10, together with a transference argument, we are able to improve the bound in (1.16) and prove the following theorem.
Theorem 1.13. Let Y be a connected analytic submanifold of
![]() ${\mathbb{R}^n\cong M_{n,1}(\mathbb{R})}$
of dimension
${\mathbb{R}^n\cong M_{n,1}(\mathbb{R})}$
of dimension
![]() $d\geqslant 2$
not contained in a rational affine hyperplane. Suppose that a continuous non-decreasing function f satisfies
$d\geqslant 2$
not contained in a rational affine hyperplane. Suppose that a continuous non-decreasing function f satisfies
Then the intersection of
![]() $\operatorname{UA}^*_{{n},1}(f)$
with Y is dense and uncountable. In particular, there exists a dense and uncountable set of totally irrational
$\operatorname{UA}^*_{{n},1}(f)$
with Y is dense and uncountable. In particular, there exists a dense and uncountable set of totally irrational
![]() $\mathbf{x} \in Y$
satisfying
$\mathbf{x} \in Y$
satisfying
![]() $\hat\omega(\mathbf{x}) \geqslant {1}/{({n}-d+1})$
.
$\hat\omega(\mathbf{x}) \geqslant {1}/{({n}-d+1})$
.
Remark 1.14. Using methods from [Reference WeissWei02] and [Reference Kleinbock, Moshchevitin and WeissKMW21] and a dynamical interpretation of uniform approximation through divergence of trajectories in the space of lattices, Datta and Tamam [Reference Datta and TamamDT24] recently proved a weighted version of Theorem 1.13 independently of the present paper and not using transference. More precisely,
-
– [Reference Datta and TamamDT24, Theorem 1.1] produces totally irrational vectors on analytic submanifolds that are singular with respect to multiple weights in the spirit of Theorem 1.7; and
-
– [Reference Datta and TamamDT24, Theorem 1.2] constructs vectors in
 $\operatorname{UA}^*_{n,1}(f, {\boldsymbol{\omega}})\cap Y$
for any weight
$\operatorname{UA}^*_{n,1}(f, {\boldsymbol{\omega}})\cap Y$
for any weight
 ${\boldsymbol{\omega}}$
and any affine subspace Y of
${\boldsymbol{\omega}}$
and any affine subspace Y of
 $\mathbb{R}^n$
not contained in a rational affine hyperplane, with optimal decay conditions on approximating functions f, which, in particular, proves Theorem 1.13 for Y being an affine subspace of
$\mathbb{R}^n$
not contained in a rational affine hyperplane, with optimal decay conditions on approximating functions f, which, in particular, proves Theorem 1.13 for Y being an affine subspace of
 $\mathbb{R}^n$
.
$\mathbb{R}^n$
.
It is likely that the above results can be derived from the main theorem of the present paper by combining Theorem 1.10 with a weighted transference argument as in [Reference ChowCGGM+20] and [Reference GermanGer20].
1.9 Other applications
In the last section of the paper we briefly survey a few other settings where our main theorem can be applied. These include: a relationship between the conclusion of our main theorem and the absence of the Kan–Moshchevitin phenomenon as exhibited in [Reference Kan and MoshchevitinKM10]; Diophantine approximation with restrictions on
![]() $\textbf{p}$
and
$\textbf{p}$
and
![]() $\textbf{q}$
; inhomogeneous approximation; and approximating subspaces of
$\textbf{q}$
; inhomogeneous approximation; and approximating subspaces of
![]() $\mathbb{R}^d$
by rational subspaces. Proofs will appear in a sequel to this paper.
$\mathbb{R}^d$
by rational subspaces. Proofs will appear in a sequel to this paper.
2. Proof of the abstract result
Proof of Theorem 1.5.Recall that the statement of the theorem involves two countable collections
![]() $\mathcal{L}$
and
$\mathcal{L}$
and
![]() $\mathcal{R}$
of subsets of Y. In the course of the proof we will index those collections by
$\mathcal{R}$
of subsets of Y. In the course of the proof we will index those collections by
![]() $\mathbb{N}$
, writing
$\mathbb{N}$
, writing
![]() $\mathcal{L} = \{L_i: i\in\mathbb{N}\}$
and
$\mathcal{L} = \{L_i: i\in\mathbb{N}\}$
and
![]() $\mathcal{R} = \{R_\ell: \ell\in\mathbb{N}\}$
. That is, we will essentially work with functions
$\mathcal{R} = \{R_\ell: \ell\in\mathbb{N}\}$
. That is, we will essentially work with functions
![]() $i \mapsto L_i$
and
$i \mapsto L_i$
and
![]() $\ell \mapsto R_\ell$
, and will not assume these functions to be injective.
$\ell \mapsto R_\ell$
, and will not assume these functions to be injective.
Take a non-empty open
![]() $W\subset Y$
, which, since Y is locally compact, we can assume to be relatively compact. We will inductively construct a nested sequence of open sets
$W\subset Y$
, which, since Y is locally compact, we can assume to be relatively compact. We will inductively construct a nested sequence of open sets
![]() $U_\ell \subseteq U_0 {\, \stackrel{\mathrm{def}}{=}\, } {W}$
, an increasing sequence
$U_\ell \subseteq U_0 {\, \stackrel{\mathrm{def}}{=}\, } {W}$
, an increasing sequence
![]() $T_\ell \to \infty$
, and a sequence of indices
$T_\ell \to \infty$
, and a sequence of indices
![]() $i_\ell$
so that for all
$i_\ell$
so that for all
![]() $\ell \in \mathbb{N}$
:
$\ell \in \mathbb{N}$
:
-
(i)
 $\varnothing\neq \overline{ U_{\ell}}\subseteq U_{\ell-1}$
;
$\varnothing\neq \overline{ U_{\ell}}\subseteq U_{\ell-1}$
; -
(ii)
 $ L_{i_\ell} \cap U_\ell \ne \varnothing$
and
$ L_{i_\ell} \cap U_\ell \ne \varnothing$
and
 ${U_\ell \cap {R_\ell} =\varnothing}$
;
${U_\ell \cap {R_\ell} =\varnothing}$
; -
(iii) for all
 $1\leqslant k \leqslant \ell$
there exists
$1\leqslant k \leqslant \ell$
there exists
 $s = s(k,\ell)\in \mathcal{I}$
such that
$s = s(k,\ell)\in \mathcal{I}$
such that
 $d_{k,s(k,\ell)}\equiv 0$
on
$d_{k,s(k,\ell)}\equiv 0$
on
 $\varphi_{k}(L_{i_\ell})$
and
$\varphi_{k}(L_{i_\ell})$
and
 $h_{k,s(k,\ell)} \leqslant T_\ell$
; and
$h_{k,s(k,\ell)} \leqslant T_\ell$
; and -
(iv) for all
 $1 \leqslant k \leqslant \ell-1$
and all
$1 \leqslant k \leqslant \ell-1$
and all
 $x \in U_{\ell},$
$x \in U_{\ell},$
 $d_{k,s(k,\ell-1)}\big(\varphi_k(x)\big) < f_k(T_{\ell})$
, where
$d_{k,s(k,\ell-1)}\big(\varphi_k(x)\big) < f_k(T_{\ell})$
, where
 $s(k,\ell-1)$
is as in (iii) (for
$s(k,\ell-1)$
is as in (iii) (for
 $\ell-1$
).
$\ell-1$
).
Step 1: Sufficiency. Let us first check that this is sufficient for part (a) of the theorem. First observe that (i) and the relative compactness of W imply that
![]() $ \bigcap\limits_{\ell \in \mathbb{N}} \overline{ U_\ell} $
is non-empty. We claim that
$ \bigcap\limits_{\ell \in \mathbb{N}} \overline{ U_\ell} $
is non-empty. We claim that
Indeed, for any k take
![]() $T\geqslant T_{k}$
, and let
$T\geqslant T_{k}$
, and let
![]() $\ell$
be such that
$\ell$
be such that
![]() $T_\ell\leqslant T < T_{\ell+1}$
; then clearly
$T_\ell\leqslant T < T_{\ell+1}$
; then clearly
![]() $\ell \geqslant k$
. Take
$\ell \geqslant k$
. Take
![]() $s = s(k,\ell)$
. Then
$s = s(k,\ell)$
. Then
![]() $h_{k,s} \leqslant T_\ell\leqslant T $
by (iii), and by (iv) and since
$h_{k,s} \leqslant T_\ell\leqslant T $
by (iii), and by (iv) and since
![]() $f_k$
is non-increasing and
$f_k$
is non-increasing and
![]() $x \in U_{\ell+1}$
, we have that
$x \in U_{\ell+1}$
, we have that
Therefore
![]() $\varphi_k(x)$
is
$\varphi_k(x)$
is
![]() $(\mathcal{X}_k,f_k)$
-uniform. Also from (ii) it follows that
$(\mathcal{X}_k,f_k)$
-uniform. Also from (ii) it follows that
![]() $x\notin \bigcup_{\ell} R_\ell$
. Thus x belongs to the set (1.11), which implies its density and finishes the proof of (a).
$x\notin \bigcup_{\ell} R_\ell$
. Thus x belongs to the set (1.11), which implies its density and finishes the proof of (a).
Step 2: Base case of induction. By the total density of
![]() $\mathcal{L}$
relative to
$\mathcal{L}$
relative to
![]() $\mathcal{R}$
there exists
$\mathcal{R}$
there exists
![]() $i_1 $
so that
$i_1 $
so that
Since
![]() $\mathcal{L}$
is aligned with
$\mathcal{L}$
is aligned with
![]() $\mathcal{X}_1$
via
$\mathcal{X}_1$
via
![]() $\varphi_1$
, there exists
$\varphi_1$
, there exists
![]() $s = s(1,1)$
such that
$s = s(1,1)$
such that
![]() $\varphi_1(L_{i_1}) $
is contained in
$\varphi_1(L_{i_1}) $
is contained in
![]() ${d_{1,s}^{-1}(\{0\})}$
. Choose
${d_{1,s}^{-1}(\{0\})}$
. Choose
![]() $T_1$
so that
$T_1$
so that
![]() $T_1 > %H_1(A){h_{1,s}}$
, and let
$T_1 > %H_1(A){h_{1,s}}$
, and let
![]() $z \in L_{i_1} \cap {W}$
. Choose a neighborhood
$z \in L_{i_1} \cap {W}$
. Choose a neighborhood
![]() $\hat{U}_1$
of z so that
$\hat{U}_1$
of z so that
![]() $\overline{\hat{U}_1} \subset{W}$
. Since
$\overline{\hat{U}_1} \subset{W}$
. Since
![]() $\mathcal{L}$
respects
$\mathcal{L}$
respects
![]() $R_1$
and the latter is closed, there is an open set
$R_1$
and the latter is closed, there is an open set
![]() $U_1 \subset\hat{U}_1$
such that
$U_1 \subset\hat{U}_1$
such that
![]() $L_{i_1} \cap U_1 \neq \varnothing$
and
$L_{i_1} \cap U_1 \neq \varnothing$
and
![]() $U_1 \cap{R_1} = \varnothing.$
This choice ensures that (ii) holds; (iii) holds by the choice of s and
$U_1 \cap{R_1} = \varnothing.$
This choice ensures that (ii) holds; (iii) holds by the choice of s and
![]() $T_1$
, and (i) holds since
$T_1$
, and (i) holds since
![]() $U_1 \subset \hat{U}_1$
and
$U_1 \subset \hat{U}_1$
and
![]() $U_0 ={W}$
. Item (iv) is vacuous for
$U_0 ={W}$
. Item (iv) is vacuous for
![]() $\ell=1$
. This completes the base case.
$\ell=1$
. This completes the base case.
Step 3: Inductive step. Assume that we have
![]() $U_\ell, T_\ell, i_\ell$
satisfying the inductive hypotheses. In view of (1.8) and (ii), there exists
$U_\ell, T_\ell, i_\ell$
satisfying the inductive hypotheses. In view of (1.8) and (ii), there exists
![]() $i_{\ell+1}$
so that
$i_{\ell+1}$
so that
Since for any
![]() $k\in\mathbb{N}$
the collection
$k\in\mathbb{N}$
the collection
![]() $\mathcal{L}$
is aligned with
$\mathcal{L}$
is aligned with
![]() $\mathcal{X}_k$
via
$\mathcal{X}_k$
via
![]() $\varphi_k$
, for each
$\varphi_k$
, for each
![]() $k = 1, \ldots, \ell+1$
there is
$k = 1, \ldots, \ell+1$
there is
![]() $s(k,\ell+1)\in \mathcal{I}$
such that
$s(k,\ell+1)\in \mathcal{I}$
such that
![]() $\varphi_k(L_{i_{\ell+1}}) \subset {d_{k,s(k,\ell+1)}^{-1}(\{0\})}$
. Let
$\varphi_k(L_{i_{\ell+1}}) \subset {d_{k,s(k,\ell+1)}^{-1}(\{0\})}$
. Let
and let
![]() $z \in L_{i_{\ell+1}} \cap L_{i_\ell} \cap U_\ell $
. Since for
$z \in L_{i_{\ell+1}} \cap L_{i_\ell} \cap U_\ell $
. Since for
![]() $k = 1, \ldots, \ell$
the functions
$k = 1, \ldots, \ell$
the functions
![]() ${d_{k,s(k,\ell)}} \circ \varphi_k$
are continuous and vanish at
${d_{k,s(k,\ell)}} \circ \varphi_k$
are continuous and vanish at
![]() $z \in L_{i_\ell}$
, there is a neighborhood
$z \in L_{i_\ell}$
, there is a neighborhood
![]() $\hat{U}_{\ell+1}$
of z such that
$\hat{U}_{\ell+1}$
of z such that
![]() $\overline{\hat{U}_{\ell+1} }\subset U_\ell$
and
$\overline{\hat{U}_{\ell+1} }\subset U_\ell$
and
Again, since
![]() $R_{\ell+1}$
is closed and is respected by
$R_{\ell+1}$
is closed and is respected by
![]() $\mathcal{L}$
, it follows that there is an open set
$\mathcal{L}$
, it follows that there is an open set
![]() $U_{\ell+1} \subset\hat{U}_{\ell+1}$
such that
$U_{\ell+1} \subset\hat{U}_{\ell+1}$
such that
This choice, and the inductive hypothesis, ensure that (ii) holds for
![]() $\ell+1$
; (iii) holds for
$\ell+1$
; (iii) holds for
![]() $\ell+1$
by the choice of
$\ell+1$
by the choice of
![]() $s(k,\ell+1)$
and
$s(k,\ell+1)$
and
![]() $T_{\ell+1}$
, and (i) and (iv) hold for
$T_{\ell+1}$
, and (i) and (iv) hold for
![]() $\ell+1$
since
$\ell+1$
since
![]() $U_{\ell+1} \subset \hat{U}_{\ell+1}$
. This finishes the proof of (a).
$U_{\ell+1} \subset \hat{U}_{\ell+1}$
. This finishes the proof of (a).
Step 4: Part (b). The second part of Theorem 1.5 follows easily from part (a). Indeed, arguing by contradiction, assume that the set (1.11) consists of countably many points
![]() $\mathcal{R}_0{\, \stackrel{\mathrm{def}}{=}\, } \{y_j: j\in\mathbb{N}\}$
. Then one can replace
$\mathcal{R}_0{\, \stackrel{\mathrm{def}}{=}\, } \{y_j: j\in\mathbb{N}\}$
. Then one can replace
![]() $\mathcal{R}$
with
$\mathcal{R}$
with
![]() $\mathcal{R}\cup \mathcal{R}_0$
which will still satisfy (1.8) and be respected by
$\mathcal{R}\cup \mathcal{R}_0$
which will still satisfy (1.8) and be respected by
![]() $\mathcal{L}$
(here we use the fact that every
$\mathcal{L}$
(here we use the fact that every
![]() $L\in\mathcal{L}$
is either connected or has no isolated points). Thus the set (1.11) with this new choice of
$L\in\mathcal{L}$
is either connected or has no isolated points). Thus the set (1.11) with this new choice of
![]() $\mathcal{R}$
will be empty, contradicting Theorem 1.5(a).
$\mathcal{R}$
will be empty, contradicting Theorem 1.5(a).
3. Simultaneous approximation
In this section we consider the standard Diophantine system
![]() $\mathcal{X}_{m,n}$
as in (1.6). We are going to apply Theorem 1.5 with
$\mathcal{X}_{m,n}$
as in (1.6). We are going to apply Theorem 1.5 with
![]() $\varphi_k = \operatorname{Id}$
for each k and with the collection
$\varphi_k = \operatorname{Id}$
for each k and with the collection
![]() $\mathcal{L}$
parametrized by the direct product of
$\mathcal{L}$
parametrized by the direct product of
![]() $\mathbb{Z}^m$
and
$\mathbb{Z}^m$
and
![]() $\mathbb{Z}^n\smallsetminus\{0\}$
. Namely we will consider the collection
$\mathbb{Z}^n\smallsetminus\{0\}$
. Namely we will consider the collection
Let us prove the following proposition.
Proposition 3.1. Let
![]() $m,n\in\mathbb{N}$
with
$m,n\in\mathbb{N}$
with
![]() $n > 1$
, and let Y be a non-empty open subset of
$n > 1$
, and let Y be a non-empty open subset of
![]() $M_{m,n}(\mathbb{R})$
. Then the collection
$M_{m,n}(\mathbb{R})$
. Then the collection
is totally dense.
Proof. Clearly
![]() $M_{m\times n}(\mathbb{Q})$
is dense in
$M_{m\times n}(\mathbb{Q})$
is dense in
![]() $M_{m,n}(\mathbb{R})$
, and, furthermore,
$M_{m,n}(\mathbb{R})$
, and, furthermore,
![]() $L_{\textbf{p},\textbf{q}}\cap M_{m\times n}(\mathbb{Q})$
is dense in
$L_{\textbf{p},\textbf{q}}\cap M_{m\times n}(\mathbb{Q})$
is dense in
![]() $L_{\textbf{p},\textbf{q}}$
for any
$L_{\textbf{p},\textbf{q}}$
for any
![]() $\textbf{q} \in\mathbb{Z}^n\smallsetminus\{0\}$
and
$\textbf{q} \in\mathbb{Z}^n\smallsetminus\{0\}$
and
![]() $\textbf{p}\in\mathbb{Z}^m$
. Moreover, any
$\textbf{p}\in\mathbb{Z}^m$
. Moreover, any
![]() $B\in M_{m\times n}(\mathbb{Q})$
lies in an
$B\in M_{m\times n}(\mathbb{Q})$
lies in an
![]() $L_{\textbf{p},\textbf{q}} $
for some
$L_{\textbf{p},\textbf{q}} $
for some
![]() $\textbf{q} \in\mathbb{Z}^n\smallsetminus\{0\}$
and
$\textbf{q} \in\mathbb{Z}^n\smallsetminus\{0\}$
and
![]() $\textbf{p}\in\mathbb{Z}^m$
. This implies (1.7). Now fix
$\textbf{p}\in\mathbb{Z}^m$
. This implies (1.7). Now fix
![]() $(\textbf{p}_0,\textbf{q}_0) \in\mathbb{Z}^m\times(\mathbb{Z}^n\smallsetminus\{0\})$
such that
$(\textbf{p}_0,\textbf{q}_0) \in\mathbb{Z}^m\times(\mathbb{Z}^n\smallsetminus\{0\})$
such that
![]() $L_{\textbf{p}_0,\textbf{q}_0}\cap Y\ne\varnothing$
, and choose an open
$L_{\textbf{p}_0,\textbf{q}_0}\cap Y\ne\varnothing$
, and choose an open
![]() $W \subset {Y}$
which intersects
$W \subset {Y}$
which intersects
![]() $L_{\textbf{p}_0,\textbf{q}_0}$
non-trivially. Then we pick an arbitrary
$L_{\textbf{p}_0,\textbf{q}_0}$
non-trivially. Then we pick an arbitrary
we let
![]() $E_B$
be the union of all the subspaces
$E_B$
be the union of all the subspaces
![]() $L_{\textbf{p},\textbf{q}}$
containing B (this clearly includes
$L_{\textbf{p},\textbf{q}}$
containing B (this clearly includes
![]() $L_{\textbf{p}_0,\textbf{q}_0}$
), and we write
$L_{\textbf{p}_0,\textbf{q}_0}$
), and we write
 $$ \begin{aligned} E_B &=\, \bigcup_{(\textbf{p},\textbf{q}) \in\mathbb{Z}^m\times(\mathbb{Z}^n\smallsetminus\{0\}): B\textbf{q} = \textbf{p}}\{A\in M_{m,n}(\mathbb{R}): A\textbf{q} = \textbf{p}\}\\ &=\, \bigcup_{\textbf{q} \in\mathbb{Z}^n\smallsetminus\{0\}, \, B\textbf{q}\in\mathbb{Z}^m}\{A\in M_{m,n}(\mathbb{R}): A\textbf{q} = B\textbf{q}\} \\ &= B + \bigcup_{\textbf{q} \in\mathbb{Z}^n\smallsetminus\{0\}, \, B\textbf{q}\in\mathbb{Z}^m}\{C\in M_{m,n}(\mathbb{R}): C\textbf{q} = 0\}. \end{aligned} $$
$$ \begin{aligned} E_B &=\, \bigcup_{(\textbf{p},\textbf{q}) \in\mathbb{Z}^m\times(\mathbb{Z}^n\smallsetminus\{0\}): B\textbf{q} = \textbf{p}}\{A\in M_{m,n}(\mathbb{R}): A\textbf{q} = \textbf{p}\}\\ &=\, \bigcup_{\textbf{q} \in\mathbb{Z}^n\smallsetminus\{0\}, \, B\textbf{q}\in\mathbb{Z}^m}\{A\in M_{m,n}(\mathbb{R}): A\textbf{q} = B\textbf{q}\} \\ &= B + \bigcup_{\textbf{q} \in\mathbb{Z}^n\smallsetminus\{0\}, \, B\textbf{q}\in\mathbb{Z}^m}\{C\in M_{m,n}(\mathbb{R}): C\textbf{q} = 0\}. \end{aligned} $$
Note that the set of
![]() $\textbf{q} \in\mathbb{Z}^n$
such that
$\textbf{q} \in\mathbb{Z}^n$
such that
![]() $B\textbf{q}\in\mathbb{Z}^m$
contains
$B\textbf{q}\in\mathbb{Z}^m$
contains
![]() $N\mathbb{Z}^n$
for some
$N\mathbb{Z}^n$
for some
![]() $N\in\mathbb{N}$
. Therefore one has
$N\in\mathbb{N}$
. Therefore one has
If
![]() $n>m$
it is clear that
$n>m$
it is clear that
![]() $E_B$
contains
$E_B$
contains
![]() $M_{m\times n}(\mathbb{Q})$
, which readily implies the total density of the collection (3.2) in an even stronger form: namely, that the union in (1.9) is dense in
$M_{m\times n}(\mathbb{Q})$
, which readily implies the total density of the collection (3.2) in an even stronger form: namely, that the union in (1.9) is dense in
![]() $M_{m,n}(\mathbb{R})$
.
$M_{m,n}(\mathbb{R})$
.
In general we see that
![]() $\overline{E_B} = B + R_{<n}$
, where
$\overline{E_B} = B + R_{<n}$
, where
which is a proper algebraic subvariety of
![]() $M_{m,n}(\mathbb{R})$
if
$M_{m,n}(\mathbb{R})$
if
![]() $n \leqslant m$
. Now let us consider the union of the sets
$n \leqslant m$
. Now let us consider the union of the sets
![]() $E_B$
over all
$E_B$
over all
![]() $B\in M_{m\times n}(\mathbb{Q})\cap L_{\textbf{p}_0,\textbf{q}_0}\cap W$
, and then take the closure, which is easily seen to have the following form:
$B\in M_{m\times n}(\mathbb{Q})\cap L_{\textbf{p}_0,\textbf{q}_0}\cap W$
, and then take the closure, which is easily seen to have the following form:
 $$\overline{\bigcup_{B\in M_{m\times n}(\mathbb{Q})\cap L_{\textbf{p}_0,\textbf{q}_0}\cap W} E_B} = \{B\in \overline{W}: B\textbf{q}_0 = \textbf{p}_0\} + R_{<n}.$$
$$\overline{\bigcup_{B\in M_{m\times n}(\mathbb{Q})\cap L_{\textbf{p}_0,\textbf{q}_0}\cap W} E_B} = \{B\in \overline{W}: B\textbf{q}_0 = \textbf{p}_0\} + R_{<n}.$$
If
![]() $n=1$
then
$n=1$
then
![]() $E_B = \{B\}$
, and the above closure coincides with
$E_B = \{B\}$
, and the above closure coincides with
![]() $ {L_{\textbf{p}_0,\textbf{q}_0}}\cap \overline{W}$
, and hence there is no total density. Now suppose that
$ {L_{\textbf{p}_0,\textbf{q}_0}}\cap \overline{W}$
, and hence there is no total density. Now suppose that
![]() $1 < n \leqslant m$
, and let
$1 < n \leqslant m$
, and let
![]() $D\in\operatorname{GL}_n(\mathbb{R})$
be such that
$D\in\operatorname{GL}_n(\mathbb{R})$
be such that
![]() $\textbf{q}_0 = D\mathbf{e}_n$
. Then one can write
$\textbf{q}_0 = D\mathbf{e}_n$
. Then one can write
since
![]() $R_{<n}$
is invariant under right-multiplication by invertible matrices. Thus it suffices to prove the claim under the assumption that
$R_{<n}$
is invariant under right-multiplication by invertible matrices. Thus it suffices to prove the claim under the assumption that
![]() $\textbf{q} = \mathbf{e}_n$
, that is, to show that for any non-empty open
$\textbf{q} = \mathbf{e}_n$
, that is, to show that for any non-empty open
![]() $W\subset M_{m,n}(\mathbb{R})$
and any
$W\subset M_{m,n}(\mathbb{R})$
and any
![]() $\textbf{p}_0\in\mathbb{Z}^m$
, the set
$\textbf{p}_0\in\mathbb{Z}^m$
, the set
![]() $\{A\in \overline{W}: A\mathbf{e}_n = \textbf{p}_0\} + R_{<n} $
contains some open neighborhood V of
$\{A\in \overline{W}: A\mathbf{e}_n = \textbf{p}_0\} + R_{<n} $
contains some open neighborhood V of
![]() $L_{\textbf{p}_0,\mathbf{e}_n} \cap W$
. For this it will be convenient to write the elements of
$L_{\textbf{p}_0,\mathbf{e}_n} \cap W$
. For this it will be convenient to write the elements of
![]() $M_{m,n}(\mathbb{R})$
in a column-vector notation. Namely, we can write
$M_{m,n}(\mathbb{R})$
in a column-vector notation. Namely, we can write
for some non-empty open subset W’ of
![]() $M_{m\times(n-1)}$
. Then it becomes clear that we can take
$M_{m\times(n-1)}$
. Then it becomes clear that we can take
simply because any matrix
![]() $[\begin{matrix} \mathbf{a}_1 & \cdots & \mathbf{a}_{n-1}& \mathbf{b}\end{matrix}]$
with
$[\begin{matrix} \mathbf{a}_1 & \cdots & \mathbf{a}_{n-1}& \mathbf{b}\end{matrix}]$
with
![]() $[\begin{matrix} \mathbf{a}_1 & \cdots & \mathbf{a}_{n-1}\end{matrix}]\in W'$
can be written as
$[\begin{matrix} \mathbf{a}_1 & \cdots & \mathbf{a}_{n-1}\end{matrix}]\in W'$
can be written as
This finishes the proof.
We can now use the above proposition to furnish the following proof.
Proof of Theorem 1.2(a).Indeed, it is clear that the collection
![]() $\mathcal{L}$
as in (3.1) is aligned with
$\mathcal{L}$
as in (3.1) is aligned with
![]() $\mathcal{X}_{m,n}$
, and its total density is provided by Proposition 3.1. Let
$\mathcal{X}_{m,n}$
, and its total density is provided by Proposition 3.1. Let
![]() $\mathcal{R}$
be the collection of all proper rational affine subspaces of
$\mathcal{R}$
be the collection of all proper rational affine subspaces of
![]() $M_{m,n}(\mathbb{R})$
. Obviously if L and R are two subspaces of a finite-dimensional vector space such that
$M_{m,n}(\mathbb{R})$
. Obviously if L and R are two subspaces of a finite-dimensional vector space such that
![]() $L\cap R$
has non-empty interior in L, then
$L\cap R$
has non-empty interior in L, then
![]() $\dim(L\cap R) = \dim(L)$
, which implies that
$\dim(L\cap R) = \dim(L)$
, which implies that
![]() $L\subset R$
. Hence
$L\subset R$
. Hence
![]() $\mathcal{L}$
respects any subspace of
$\mathcal{L}$
respects any subspace of
![]() $M_{m,n}(\mathbb{R})$
. This verifies all the conditions of Theorem 1.5; since elements of
$M_{m,n}(\mathbb{R})$
. This verifies all the conditions of Theorem 1.5; since elements of
![]() $\mathcal{L}$
have no isolated points, part (ii) implies the uncountability of
$\mathcal{L}$
have no isolated points, part (ii) implies the uncountability of
![]() $\operatorname{UA}^*_{m,n}(f)$
for any positive non-increasing f.
$\operatorname{UA}^*_{m,n}(f)$
for any positive non-increasing f.
More generally, one can strengthen Theorem 1.2(a) using the fact that
![]() $\mathcal{L}$
respects closed analytic submanifolds of
$\mathcal{L}$
respects closed analytic submanifolds of
![]() $M_{m,n}(\mathbb{R})$
. Recall that
$M_{m,n}(\mathbb{R})$
. Recall that
![]() ${\Psi}: U\to \mathbb{R}^k$
, where U is an open subset of
${\Psi}: U\to \mathbb{R}^k$
, where U is an open subset of
![]() $\mathbb{R}^d$
with
$\mathbb{R}^d$
with
![]() $d \leqslant k$
, is called a real analytic immersion if it is injective, each of its coordinate functions
$d \leqslant k$
, is called a real analytic immersion if it is injective, each of its coordinate functions
![]() ${\Psi}_i :U\to \mathbb{R} \ (i=1, \ldots, k)$
is infinitely differentiable, the Taylor series of each
${\Psi}_i :U\to \mathbb{R} \ (i=1, \ldots, k)$
is infinitely differentiable, the Taylor series of each
![]() ${\Psi}_i$
converges in a neighborhood of every
${\Psi}_i$
converges in a neighborhood of every
![]() $\mathbf{x} \in U$
, and the derivative mapping
$\mathbf{x} \in U$
, and the derivative mapping
![]() $d_{\mathbf{x}}{\Psi}: \mathbb{R}^d \to \mathbb{R}^k$
has rank d. By a d-dimensional real analytic submanifold of
$d_{\mathbf{x}}{\Psi}: \mathbb{R}^d \to \mathbb{R}^k$
has rank d. By a d-dimensional real analytic submanifold of
![]() $\mathbb{R}^k$
we mean a subset
$\mathbb{R}^k$
we mean a subset
![]() $Y \subset \mathbb{R}^k$
such that for every
$Y \subset \mathbb{R}^k$
such that for every
![]() $\mathbf{y} \in Y$
there is a neighborhood
$\mathbf{y} \in Y$
there is a neighborhood
![]() $V\subset \mathbb{R}^k$
containing
$V\subset \mathbb{R}^k$
containing
![]() $\mathbf{y}$
, an open set
$\mathbf{y}$
, an open set
![]() $U \subset \mathbb{R}^d$
, and a real analytic immersion
$U \subset \mathbb{R}^d$
, and a real analytic immersion
![]() ${\Psi}: U \to \mathbb{R}^k$
such that
${\Psi}: U \to \mathbb{R}^k$
such that
![]() ${V} \cap {Y} = {\Psi}({U}).$
${V} \cap {Y} = {\Psi}({U}).$
The crucial property, which distinguishes real analytic submanifolds from smooth manifolds and follows easily from the definitions, is given in the following lemma.
Lemma 3.2. Let L and R be real analytic submanifolds of
![]() $\mathbb{R}^k$
, equipped with the topology they inherit as subsets of
$\mathbb{R}^k$
, equipped with the topology they inherit as subsets of
![]() $\mathbb{R}^k$
. Suppose that L is connected, R is closed, and
$\mathbb{R}^k$
. Suppose that L is connected, R is closed, and
![]() $L \cap R$
has non-empty interior in L. Then
$L \cap R$
has non-empty interior in L. Then
![]() $L \subset R$
.
$L \subset R$
.
To make the paper self-contained we provide the proof of this lemma.
Proof. Let
![]() $d_1, d_2$
denote the dimensions of L and R. Since
$d_1, d_2$
denote the dimensions of L and R. Since
![]() $L\cap R$
has non-empty interior in L, by invariance of dimension under immersions, we have
$L\cap R$
has non-empty interior in L, by invariance of dimension under immersions, we have
![]() $d_1 \leqslant d_2$
. Let W denote the interior (in L) of
$d_1 \leqslant d_2$
. Let W denote the interior (in L) of
![]() $L \cap R$
. If W is closed (in L), then by connectedness of L we have
$L \cap R$
. If W is closed (in L), then by connectedness of L we have
![]() $L = W$
, and hence
$L = W$
, and hence
![]() $L \subset R$
and there is nothing to prove. We will assume that W is not closed in L and derive a contradiction.
$L \subset R$
and there is nothing to prove. We will assume that W is not closed in L and derive a contradiction.
Let
![]() $p \in \overline{W} \smallsetminus W$
. Since the closure is taken in L we have
$p \in \overline{W} \smallsetminus W$
. Since the closure is taken in L we have
![]() $p \in L$
, and since R is closed we have
$p \in L$
, and since R is closed we have
![]() $p \in R$
. By the real analyticity of L and R, there are open subsets
$p \in R$
. By the real analyticity of L and R, there are open subsets
![]() $U_1 \subset \mathbb{R}^{d_1}, \, U_2 \subset \mathbb{R}^{d_2}$
and real analytic immerions
$U_1 \subset \mathbb{R}^{d_1}, \, U_2 \subset \mathbb{R}^{d_2}$
and real analytic immerions
![]() $\Psi_i: U_i \to \mathbb{R}^k$
such that
$\Psi_i: U_i \to \mathbb{R}^k$
such that
![]() $\Psi_1$
parametrizes a neighborhood of p in L, and
$\Psi_1$
parametrizes a neighborhood of p in L, and
![]() $\Psi_2$
parametrizes a neighborhood of p in R. For
$\Psi_2$
parametrizes a neighborhood of p in R. For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $p_i \in U_i$
such that
$p_i \in U_i$
such that
![]() $\Psi_i(p_i) = p$
, and let
$\Psi_i(p_i) = p$
, and let
![]() $W_i = \Psi_i^{-1}(W)$
. Then
$W_i = \Psi_i^{-1}(W)$
. Then
![]() $p_1$
belongs to the closure of
$p_1$
belongs to the closure of
![]() $W_1$
in
$W_1$
in
![]() $U_1$
, and
$U_1$
, and
![]() $W_1$
is open in
$W_1$
is open in
![]() $U_1$
; thus by the uniqueness of analytic continuation (see [Reference Krantz and ParksKP92, 1.2] or [Reference Kobayashi and NomizuKN63, VI.6]),
$U_1$
; thus by the uniqueness of analytic continuation (see [Reference Krantz and ParksKP92, 1.2] or [Reference Kobayashi and NomizuKN63, VI.6]),
![]() $\Psi_i$
is uniquely determined in a neighborhood of p by
$\Psi_i$
is uniquely determined in a neighborhood of p by
![]() $\Psi_1|_{W_1}$
. In particular, L is uniquely determined in a neighborhood of p by W.
$\Psi_1|_{W_1}$
. In particular, L is uniquely determined in a neighborhood of p by W.
By the inverse function theorem for real analytic immersions (see [Reference Krantz and ParksKP92, 1.8]), there is a real analytic inverse
![]() $\Psi_2^{-1} $
to
$\Psi_2^{-1} $
to
![]() $\Psi_2$
. In an abuse of notation, denote by
$\Psi_2$
. In an abuse of notation, denote by
![]() $\mathbb{R}^{d_1}$
the coordinate plane in
$\mathbb{R}^{d_1}$
the coordinate plane in
![]() $\mathbb{R}^{d_2}$
defined as
$\mathbb{R}^{d_2}$
defined as
By making
![]() $U_2$
smaller and by replacing
$U_2$
smaller and by replacing
![]() $U_2$
with its image under a real analytic diffeomorphism, we can assume that
$U_2$
with its image under a real analytic diffeomorphism, we can assume that
![]() $W_2$
is open in
$W_2$
is open in
![]() $U_2 \cap \mathbb{R}^{d_1}$
; indeed, to see that such a change of variables exists, see [Reference Krantz and ParksKP92, Proof of Theorem1.9.5]. Once again, using the uniqueness of analytic continuation of
$U_2 \cap \mathbb{R}^{d_1}$
; indeed, to see that such a change of variables exists, see [Reference Krantz and ParksKP92, Proof of Theorem1.9.5]. Once again, using the uniqueness of analytic continuation of
![]() $\Psi_2|_{W_2}$
, we see that
$\Psi_2|_{W_2}$
, we see that
![]() $\Psi_2|_{U_2 \cap \mathbb{R}^{d_1}}$
is determined by
$\Psi_2|_{U_2 \cap \mathbb{R}^{d_1}}$
is determined by
![]() $\Psi_2|_{W_2}$
. Since the two analytic continuations agree, we see that p belongs to the interior of
$\Psi_2|_{W_2}$
. Since the two analytic continuations agree, we see that p belongs to the interior of
![]() $L \cap R$
.
$L \cap R$
.
Arguing as in the above proof of Theorem 1.2(a), we arrive at the following.
Theorem 3.3. Let
![]() $m,n\in\mathbb{N}$
with
$m,n\in\mathbb{N}$
with
![]() $n > 1$
, and let a non-increasing function
$n > 1$
, and let a non-increasing function
![]() $f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
and an arbitrary countable collection
$f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
and an arbitrary countable collection
![]() $\{R_\ell\}$
of proper closed analytic submanifolds of
$\{R_\ell\}$
of proper closed analytic submanifolds of
![]() $M_{m,n}(\mathbb{R})$
be given. Then
$M_{m,n}(\mathbb{R})$
be given. Then
![]() $\operatorname{UA}_{m,n}(f) \smallsetminus \cup_{\ell} R_\ell$
is uncountable and dense in
$\operatorname{UA}_{m,n}(f) \smallsetminus \cup_{\ell} R_\ell$
is uncountable and dense in
![]() $M_{m,n}(\mathbb{R})$
.
$M_{m,n}(\mathbb{R})$
.
Likewise, for any weight vector
![]() $ {\boldsymbol{\omega}} = ({\boldsymbol{\alpha}},{\boldsymbol{\beta}}) \in \mathbb{R}_{>0}^{m+n}$
as in § 1.4, in view of (1.13) the conclusion of the above theorem holds verbatim for the set
$ {\boldsymbol{\omega}} = ({\boldsymbol{\alpha}},{\boldsymbol{\beta}}) \in \mathbb{R}_{>0}^{m+n}$
as in § 1.4, in view of (1.13) the conclusion of the above theorem holds verbatim for the set
![]() $\operatorname{UA}_{m,n}(f, {\boldsymbol{\omega}}) $
. Moreover, one can take a subset
$\operatorname{UA}_{m,n}(f, {\boldsymbol{\omega}}) $
. Moreover, one can take a subset
![]() $\mathcal{W}$
of
$\mathcal{W}$
of
![]() $\mathbb{R}_{>0}^{m+n}$
and say that
$\mathbb{R}_{>0}^{m+n}$
and say that
![]() $A\in M_{m,n}(\mathbb{R})$
is
$A\in M_{m,n}(\mathbb{R})$
is
![]() $(f, \mathcal{W})$
-uniform, denoted with some abuse of notation by
$(f, \mathcal{W})$
-uniform, denoted with some abuse of notation by
![]() $A\in \operatorname{UA}_{m,n}(f, \mathcal{W})$
, if for every sufficiently large t one can find
$A\in \operatorname{UA}_{m,n}(f, \mathcal{W})$
, if for every sufficiently large t one can find
![]() $\textbf{q} \in \mathbb{Z}^n\smallsetminus\{0\}$
and
$\textbf{q} \in \mathbb{Z}^n\smallsetminus\{0\}$
and
![]() $\textbf{p} \in \mathbb{Z}^m$
such that for any
$\textbf{p} \in \mathbb{Z}^m$
such that for any
![]() ${{\boldsymbol{\omega}} = ({\boldsymbol{\alpha}},{\boldsymbol{\beta}})}\in \mathcal{W}$
the inequalities (1.12) hold. Clearly this is stronger than being
${{\boldsymbol{\omega}} = ({\boldsymbol{\alpha}},{\boldsymbol{\beta}})}\in \mathcal{W}$
the inequalities (1.12) hold. Clearly this is stronger than being
![]() $(f, {\boldsymbol{\omega}})$
-uniform for any
$(f, {\boldsymbol{\omega}})$
-uniform for any
![]() ${\boldsymbol{\omega}}\in\mathcal{W}$
. The next statement follows from Theorem 1.5 as easily as the previous one did. It immediately implies both parts of Theorem 1.7.
${\boldsymbol{\omega}}\in\mathcal{W}$
. The next statement follows from Theorem 1.5 as easily as the previous one did. It immediately implies both parts of Theorem 1.7.
Theorem 3.4. Let
![]() $m,n\in\mathbb{N}$
with
$m,n\in\mathbb{N}$
with
![]() $n > 1$
. Suppose that for any
$n > 1$
. Suppose that for any
![]() $k\in\mathbb{N}$
we are given a non-increasing function
$k\in\mathbb{N}$
we are given a non-increasing function
![]() $f_k: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
and a subset
$f_k: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
and a subset
![]() $\mathcal{W}_k$
of
$\mathcal{W}_k$
of
![]() $ \mathbb{R}_{>0}^{m+n}$
such that
$ \mathbb{R}_{>0}^{m+n}$
such that
Then for any countable collection
![]() $\{R_\ell \}$
of proper analytic submanifolds of
$\{R_\ell \}$
of proper analytic submanifolds of
![]() $M_{m,n}(\mathbb{R})$
, the set
$M_{m,n}(\mathbb{R})$
, the set
is uncountable and dense in
![]() $M_{m,n}(\mathbb{R})$
. In particular, the set
$M_{m,n}(\mathbb{R})$
. In particular, the set
is uncountable and dense in
![]() $M_{m,n}(\mathbb{R})$
for any
$M_{m,n}(\mathbb{R})$
for any
![]() $\{R_\ell\}$
as above and any non-increasing positive function f.
$\{R_\ell\}$
as above and any non-increasing positive function f.
Proof. Again we take
![]() $Y = M_{m,n}(\mathbb{R}) = X_k$
,
$Y = M_{m,n}(\mathbb{R}) = X_k$
,
![]() $ \mathcal{I} = \mathbb{Z}^m\times (\mathbb{Z}^n\smallsetminus\{0\})$
, and
$ \mathcal{I} = \mathbb{Z}^m\times (\mathbb{Z}^n\smallsetminus\{0\})$
, and
![]() $\varphi_k = \operatorname{Id}$
for each k, and, to define the Diophantine systems associated with each
$\varphi_k = \operatorname{Id}$
for each k, and, to define the Diophantine systems associated with each
![]() $X_k$
, we let
$X_k$
, we let
Because of (3.3), for any
![]() $(\textbf{p},\textbf{q})$
and any k the value
$(\textbf{p},\textbf{q})$
and any k the value
![]() $h_{k,(\textbf{p},\textbf{q})}$
is finite and the function
$h_{k,(\textbf{p},\textbf{q})}$
is finite and the function
![]() $d_{k,(\textbf{p},\textbf{q})}$
is continuous. Thus the same argument, in view of Remark 1.6(2), yields the proof of the first part of the theorem. For the ‘in particular’ part one simply writes
$d_{k,(\textbf{p},\textbf{q})}$
is continuous. Thus the same argument, in view of Remark 1.6(2), yields the proof of the first part of the theorem. For the ‘in particular’ part one simply writes
![]() $\mathbb{R}_{>0}^{m+n}$
as the union of countably many subsets
$\mathbb{R}_{>0}^{m+n}$
as the union of countably many subsets
![]() $\mathcal{W}_k$
satisfying (3.3).
$\mathcal{W}_k$
satisfying (3.3).
4. Uniformly approximable row vectors on analytic submanifolds and some fractals
Our next goal is to apply Theorem 1.5 to study uniform approximation on submanifolds Y of
![]() $M_{m,n}(\mathbb{R})$
. It is clear that the method we are using in this paper (which is essentially Khintchine’s original argument) is not applicable if
$M_{m,n}(\mathbb{R})$
. It is clear that the method we are using in this paper (which is essentially Khintchine’s original argument) is not applicable if
![]() $\dim Y = 1$
; indeed, there are very few results in the literature dealing with singular vectors on curves, and many open questions (see e.g. [Reference Poëls and RoyPR22] and the references therein). However, the method does work if
$\dim Y = 1$
; indeed, there are very few results in the literature dealing with singular vectors on curves, and many open questions (see e.g. [Reference Poëls and RoyPR22] and the references therein). However, the method does work if
![]() $m=1$
, Y is a connected analytic submanifold of
$m=1$
, Y is a connected analytic submanifold of
![]() $\mathbb{R}^n\cong M_{1,n}(\mathbb{R})$
, and the dimension of Y is at least 2 (see Theorem 1.8).
$\mathbb{R}^n\cong M_{1,n}(\mathbb{R})$
, and the dimension of Y is at least 2 (see Theorem 1.8).
In this section we will generalize the aforementioned theorem, but first let us observe that the situation gets more complicated when
![]() $\min(m,n) > 1$
. The next proposition gives an example of a three-dimensional submanifold (in fact, an affine subspace) of
$\min(m,n) > 1$
. The next proposition gives an example of a three-dimensional submanifold (in fact, an affine subspace) of
![]() $M_{2,2}(\mathbb{R})$
which does not contain any f-uniform matrices if f decays rapidly enough. Let us recall that a real number
$M_{2,2}(\mathbb{R})$
which does not contain any f-uniform matrices if f decays rapidly enough. Let us recall that a real number
![]() $\alpha$
is badly approximable if
$\alpha$
is badly approximable if
Proposition 4.1. Let
![]() $\alpha\in \mathbb{R}$
be a badly approximable number, let
$\alpha\in \mathbb{R}$
be a badly approximable number, let
![]() $\lambda = {(\sqrt{5}+3)}/{2}$
, and let Y be the set of
$\lambda = {(\sqrt{5}+3)}/{2}$
, and let Y be the set of
![]() $2\times2$
matrices of the form
$2\times2$
matrices of the form
![]() $A = \Big(\begin{array}{cc}\alpha &* \cr* & *\end{array}\Big)$
. Then
$A = \Big(\begin{array}{cc}\alpha &* \cr* & *\end{array}\Big)$
. Then
![]() $\hat{\omega}(A)\leqslant \lambda$
for any totally irrational
$\hat{\omega}(A)\leqslant \lambda$
for any totally irrational
![]() $A\in Y$
; that is, no totally irrational
$A\in Y$
; that is, no totally irrational
![]() $A\in Y$
is f-uniform as long as f decays faster than
$A\in Y$
is f-uniform as long as f decays faster than
![]() $\phi_{\lambda+\varepsilon}$
for some
$\phi_{\lambda+\varepsilon}$
for some
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
Proof. We need to recall the notion of an ordinary Diophantine exponent, which is an asymptotic version of (1.5); namely,

where the distance is computed using the supremum norm on
![]() $\mathbb{R}^m$
. It follows from (4.1) that
$\mathbb{R}^m$
. It follows from (4.1) that
![]() $\omega(\alpha) \leqslant 1$
. Take an arbitrary
$\omega(\alpha) \leqslant 1$
. Take an arbitrary
![]() $\beta\in\mathbb{R}$
such that
$\beta\in\mathbb{R}$
such that
![]() $1,\alpha,\beta$
are linearly independent over
$1,\alpha,\beta$
are linearly independent over
![]() $\mathbb{Q}$
, and consider
$\mathbb{Q}$
, and consider
![]() $\mathbf{v} = \Big(\begin{array}{cc}\alpha \cr\beta\end{array}\Big)$
. Clearly we have
$\mathbf{v} = \Big(\begin{array}{cc}\alpha \cr\beta\end{array}\Big)$
. Clearly we have
hence
![]() $\omega(\mathbf{v}) \leqslant 1$
as well.
$\omega(\mathbf{v}) \leqslant 1$
as well.
Now we will use the inequalities due to Jarník relating the ordinary and the uniform exponents of
![]() $\mathbf{v}$
and
$\mathbf{v}$
and
![]() $\mathbf{v}^T$
:
$\mathbf{v}^T$
:
and
(see [Reference JarníkJar38] and [Reference JarníkJar54] respectively). It follows from (4.2) that
![]() $\hat{\omega}(\mathbf{v})\leqslant {(\sqrt{5}-1)}/{2},$
and from (4.3) we can obtain
$\hat{\omega}(\mathbf{v})\leqslant {(\sqrt{5}-1)}/{2},$
and from (4.3) we can obtain
![]() $\hat{\omega}(\mathbf{v}^T) \leqslant {(\sqrt{5}+3)}/{2} = \lambda.$
Thus for any
$\hat{\omega}(\mathbf{v}^T) \leqslant {(\sqrt{5}+3)}/{2} = \lambda.$
Thus for any
![]() $A\in M_{2,2}(\mathbb{R})$
with
$A\in M_{2,2}(\mathbb{R})$
with
![]() $(\alpha,\beta)$
as its row vector we have
$(\alpha,\beta)$
as its row vector we have
![]() $\hat{\omega}(A)\leqslant \hat{\omega}(\mathbf{v}^T) \leqslant \lambda.$
$\hat{\omega}(A)\leqslant \hat{\omega}(\mathbf{v}^T) \leqslant \lambda.$
Our next result shows that such examples are impossible when
![]() $m=1$
and the dimension d of the submanifold Y of
$m=1$
and the dimension d of the submanifold Y of
![]() $\mathbb{R}^n\cong M_{1,n}$
is at least 2. Furthermore, we will exhibit vectors in Y which are f-uniform of order
$\mathbb{R}^n\cong M_{1,n}$
is at least 2. Furthermore, we will exhibit vectors in Y which are f-uniform of order
![]() $d-1$
, as defined in § 1.5.
$d-1$
, as defined in § 1.5.
Theorem 4.2. Let
![]() $n\geqslant 2$
, let Y be a d-dimensional connected analytic submanifold of
$n\geqslant 2$
, let Y be a d-dimensional connected analytic submanifold of
![]() $\mathbb{R}^n$
, where
$\mathbb{R}^n$
, where
![]() $d\geqslant 2$
, and let
$d\geqslant 2$
, and let
![]() $1\leqslant g \leqslant d-1$
. Suppose we are given an arbitrary non-increasing function
$1\leqslant g \leqslant d-1$
. Suppose we are given an arbitrary non-increasing function
![]() $f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
and a countable collection
$f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
and a countable collection
![]() $\{R_\ell \}$
of proper closed analytic submanifolds of Y. Then the set
$\{R_\ell \}$
of proper closed analytic submanifolds of Y. Then the set
is uncountable and dense in Y. In particular, if one in addition assumes that Y is not contained in any proper rational affine subspace of
![]() $\mathbb{R}^n$
, then the set
$\mathbb{R}^n$
, then the set
![]() $Y\cap \operatorname{UA}^*_{1,n}(f;g) % \smallsetminus \bigcup % _{\ell\in\N} R_\ell $
is uncountable and dense in Y.
$Y\cap \operatorname{UA}^*_{1,n}(f;g) % \smallsetminus \bigcup % _{\ell\in\N} R_\ell $
is uncountable and dense in Y.
To prove Theorem 4.2 we first need to describe the Diophantine system responsible for approximation of order g. Unwrapping Definition 1.9, we can easily see that
![]() $\mathbf{x}\in\mathbb{R}^n$
is f-uniform of order g if and only if it is
$\mathbf{x}\in\mathbb{R}^n$
is f-uniform of order g if and only if it is
![]() $(\mathcal{X},f)$
-uniform, where
$(\mathcal{X},f)$
-uniform, where
![]() $\mathcal{X}$
is the Diophantine system given by
$\mathcal{X}$
is the Diophantine system given by
 \begin{equation}{ \begin{aligned}X = \mathbb{R}^n,\ \ & \mathcal{I} = \mathbb{Z}^g \times \big((\mathbb{Z}^n)^g\smallsetminus\{\text{linearly dependent} \textit{g}-\text{tuples}\}\big),\\ &\qquad h_{p_1, \dots, p_g,\mathbf{q}_1, \ldots, \mathbf{q}_g} = \max_{i=1,\dots,g}\| \mathbf{q}_i \| ,\\ \ &d_{p_1, \dots, p_g,\mathbf{q}_1, \dots, \mathbf{q}_g}(\mathbf{x}) = \max_{i=1,\dots,g} | \mathbf{q}_i \cdot \mathbf{x} -p_i| {.}\quad\end{aligned}}\end{equation}
\begin{equation}{ \begin{aligned}X = \mathbb{R}^n,\ \ & \mathcal{I} = \mathbb{Z}^g \times \big((\mathbb{Z}^n)^g\smallsetminus\{\text{linearly dependent} \textit{g}-\text{tuples}\}\big),\\ &\qquad h_{p_1, \dots, p_g,\mathbf{q}_1, \ldots, \mathbf{q}_g} = \max_{i=1,\dots,g}\| \mathbf{q}_i \| ,\\ \ &d_{p_1, \dots, p_g,\mathbf{q}_1, \dots, \mathbf{q}_g}(\mathbf{x}) = \max_{i=1,\dots,g} | \mathbf{q}_i \cdot \mathbf{x} -p_i| {.}\quad\end{aligned}}\end{equation}
Note that the zero locus of
![]() $d_{p_1, \dots, p_g,\mathbf{q}_1, \dots, \mathbf{q}_g}$
is precisely the intersection of g rational affine hyperplanes
$d_{p_1, \dots, p_g,\mathbf{q}_1, \dots, \mathbf{q}_g}$
is precisely the intersection of g rational affine hyperplanes
![]() $L_{p_i, \textbf{q}_i}$
, which is a codimension g rational affine subspace of
$L_{p_i, \textbf{q}_i}$
, which is a codimension g rational affine subspace of
![]() $\mathbb{R}^n$
; moreover, any rational affine subspace of
$\mathbb{R}^n$
; moreover, any rational affine subspace of
![]() $\mathbb{R}^n$
of codimension g can be (in many different ways) written as such an intersection. Consequently, the collection
$\mathbb{R}^n$
of codimension g can be (in many different ways) written as such an intersection. Consequently, the collection
![]() $\mathcal L$
of all rational affine subspaces of
$\mathcal L$
of all rational affine subspaces of
![]() $\mathbb{R}^n$
of codimension g is aligned with
$\mathbb{R}^n$
of codimension g is aligned with
![]() $\mathcal{X}$
as in (4.5). It is trivial to check that
$\mathcal{X}$
as in (4.5). It is trivial to check that
![]() $\mathcal L$
is totally dense and respects any closed analytic submanifold of
$\mathcal L$
is totally dense and respects any closed analytic submanifold of
![]() $\mathbb{R}^n$
. Hence the case
$\mathbb{R}^n$
. Hence the case
![]() $Y = \mathbb{R}^n$
of Theorem 4.2 easily follows from Theorem 1.5. Let us now prove the general case where Y is an arbitrary d-dimensional analytic submanifold of
$Y = \mathbb{R}^n$
of Theorem 4.2 easily follows from Theorem 1.5. Let us now prove the general case where Y is an arbitrary d-dimensional analytic submanifold of
![]() $\mathbb{R}^n$
. For the proof we will need the following lemma.
$\mathbb{R}^n$
. For the proof we will need the following lemma.
Lemma 4.3. Let Y be a d-dimensional
![]() $C^1$
embedded submanifold of
$C^1$
embedded submanifold of
![]() $\mathbb{R}^n$
, where
$\mathbb{R}^n$
, where
![]() $d\geqslant 2$
, and let
$d\geqslant 2$
, and let
![]() $1\leqslant g \leqslant d-1$
. Then for any
$1\leqslant g \leqslant d-1$
. Then for any
![]() $\mathbf{y} \in Y$
there exists an open subset W of
$\mathbf{y} \in Y$
there exists an open subset W of
![]() $\mathbb{R}^n$
containing
$\mathbb{R}^n$
containing
![]() $\mathbf{y}$
and a totally dense (in
$\mathbf{y}$
and a totally dense (in
![]() $Y\cap W$
) collection
$Y\cap W$
) collection
![]() $\mathcal{L}_{W}$
consisting of intersections of rational affine subspaces of
$\mathcal{L}_{W}$
consisting of intersections of rational affine subspaces of
![]() $\mathbb{R}^n$
of codimension g with
$\mathbb{R}^n$
of codimension g with
![]() $Y\cap W$
.
$Y\cap W$
.
Proof. For any
![]() $\mathbf{y} \in Y$
one can choose a neighborhood
$\mathbf{y} \in Y$
one can choose a neighborhood
![]() $V\subset \mathbb{R}^n$
containing
$V\subset \mathbb{R}^n$
containing
![]() $\mathbf{y}$
, an open set
$\mathbf{y}$
, an open set
![]() $U \subset \mathbb{R}^d$
, and a differentiable embedding
$U \subset \mathbb{R}^d$
, and a differentiable embedding
![]() ${\Psi}: U \to \mathbb{R}^n$
such that
${\Psi}: U \to \mathbb{R}^n$
such that
![]() ${V} \cap {Y} ={\Psi}({U})$
. Let
${V} \cap {Y} ={\Psi}({U})$
. Let
![]() $\mathbf{x}\in U$
be such that
$\mathbf{x}\in U$
be such that
![]() ${\Psi}(\mathbf{x})=\mathbf{y}$
; then
${\Psi}(\mathbf{x})=\mathbf{y}$
; then
![]() $d_{\mathbf{x}}{\Psi}$
has rank d, and by permuting coordinates in
$d_{\mathbf{x}}{\Psi}$
has rank d, and by permuting coordinates in
![]() $\mathbb{R}^n$
without loss of generality we can assume that the leftmost
$\mathbb{R}^n$
without loss of generality we can assume that the leftmost
![]() $d\times d$
submatrix of
$d\times d$
submatrix of
![]() $d_{\mathbf{x}} {\Psi}$
is non-singular. Then, in view of the implicit function theorem, we can choose an open subset W of B containing
$d_{\mathbf{x}} {\Psi}$
is non-singular. Then, in view of the implicit function theorem, we can choose an open subset W of B containing
![]() $\mathbf{y}$
such that
$\mathbf{y}$
such that
where O is an open ball in
![]() $\mathbb{R}^d$
and
$\mathbb{R}^d$
and
![]() $\psi:O \to \mathbb{R}^{n-d}$
is a differentiable function.
$\psi:O \to \mathbb{R}^{n-d}$
is a differentiable function.
Now define
where
Equivalently,
![]() $L_M \cap W\cap Y$
can be written as
$L_M \cap W\cap Y$
can be written as
Since
![]() $d\geqslant 2$
and
$d\geqslant 2$
and
![]() $1\leqslant g \leqslant d-1$
, the collection
$1\leqslant g \leqslant d-1$
, the collection
is totally dense in O, which immediately implies that
![]() $\mathcal{L}_{W}$
is totally dense in
$\mathcal{L}_{W}$
is totally dense in
![]() $Y\cap W$
.
$Y\cap W$
.
Proof of Theorem 4.2. Our goal is to apply Theorem 1.5 locally in the neighborhood of any given point
![]() $\mathbf{y}\in Y$
. Choose an open subset W of
$\mathbf{y}\in Y$
. Choose an open subset W of
![]() $\mathbb{R}^n$
containing
$\mathbb{R}^n$
containing
![]() $\mathbf{y}$
and a collection
$\mathbf{y}$
and a collection
![]() $\mathcal{L}_{W}$
as in the above lemma. Since
$\mathcal{L}_{W}$
as in the above lemma. Since
![]() $L_M$
as in (4.6) is a codimension g rational affine subspace of
$L_M$
as in (4.6) is a codimension g rational affine subspace of
![]() $\mathbb{R}^n$
, it is clear that
$\mathbb{R}^n$
, it is clear that
![]() $\mathcal L$
is aligned with the Diophantine system (4.5). Now let us recall that Y was assumed to be an analytic manifold; hence the map
$\mathcal L$
is aligned with the Diophantine system (4.5). Now let us recall that Y was assumed to be an analytic manifold; hence the map
![]() $\psi$
is real analytic, and therefore every
$\psi$
is real analytic, and therefore every
![]() $L_M \cap W\cap Y$
is a connected analytic submanifold of
$L_M \cap W\cap Y$
is a connected analytic submanifold of
![]() $W\cap Y$
. If R is a closed analytic submanifold of Y such that
$W\cap Y$
. If R is a closed analytic submanifold of Y such that
![]() $L_M \cap W\cap R$
has non-empty interior in
$L_M \cap W\cap R$
has non-empty interior in
![]() $L_M \cap W$
, it follows that
$L_M \cap W$
, it follows that
![]() $L_M\subset W\cap R$
, which, in view of Lemma 3.2, implies that
$L_M\subset W\cap R$
, which, in view of Lemma 3.2, implies that
![]() $L_M \subset R$
. Hence
$L_M \subset R$
. Hence
![]() $\mathcal{L}_W$
respects R, and we can apply Theorem 1.5(b) and conclude that the intersection of the set (4.4) with W is uncountable, finishing the proof of the theorem.
$\mathcal{L}_W$
respects R, and we can apply Theorem 1.5(b) and conclude that the intersection of the set (4.4) with W is uncountable, finishing the proof of the theorem.
Let us now show that the same method can produce uniformly approximable vectors on certain fractals. Below is an example from [Reference Kleinbock, Moshchevitin and WeissKMW21].
Theorem 4.4. Let
![]() $n \geqslant 2$
and let
$n \geqslant 2$
and let
![]() $Y_1, \ldots, Y_n$
be perfect subsets of
$Y_1, \ldots, Y_n$
be perfect subsets of
![]() $\mathbb{R}$
such that
$\mathbb{R}$
such that
Let
![]() $Y = \prod_{j=1}^n Y_j$
. Suppose we are given an arbitrary non-increasing function
$Y = \prod_{j=1}^n Y_j$
. Suppose we are given an arbitrary non-increasing function
![]() $f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
and a countable collection
$f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
and a countable collection
![]() $\{R_\ell \}$
of proper closed analytic submanifolds of
$\{R_\ell \}$
of proper closed analytic submanifolds of
![]() $\mathbb{R}^n$
. Then
$\mathbb{R}^n$
. Then
is uncountable and dense in Y. In particular,
![]() $Y\cap \operatorname{UA}^*_{1,n}(f%;g ) % \smallsetminus \bigcup % _{\ell\in\N} R_\ell $
is uncountable and dense in Y.
$Y\cap \operatorname{UA}^*_{1,n}(f%;g ) % \smallsetminus \bigcup % _{\ell\in\N} R_\ell $
is uncountable and dense in Y.
Proof. Let
![]() $\mathbf{e}_1, \ldots, \mathbf{e}_n$
be the standard basis vectors in
$\mathbf{e}_1, \ldots, \mathbf{e}_n$
be the standard basis vectors in
![]() $\mathbb{R}^n$
, and let
$\mathbb{R}^n$
, and let
![]() $\{A_i\} $
be the collection of all rational affine hyperplanes of
$\{A_i\} $
be the collection of all rational affine hyperplanes of
![]() $\mathbb{R}^n$
which are normal to one of
$\mathbb{R}^n$
which are normal to one of
![]() $\mathbf{e}_1$
and
$\mathbf{e}_1$
and
![]() $\mathbf{e}_2$
and have non-trivial intersection with Y; that is, each of the
$\mathbf{e}_2$
and have non-trivial intersection with Y; that is, each of the
![]() $A_i$
is of the form
$A_i$
is of the form
note that necessarily we have
![]() $r_i\in {Y_{k_i}}$
. We claim that the collection
$r_i\in {Y_{k_i}}$
. We claim that the collection
![]() $\{ Y \cap A_i\}$
, which is obviously aligned with
$\{ Y \cap A_i\}$
, which is obviously aligned with
![]() $\mathcal{X}_{1,n}$
, is totally dense. Indeed, (1.7) clearly follows from (4.8). To prove (1.9), take an open subset W of
$\mathcal{X}_{1,n}$
, is totally dense. Indeed, (1.7) clearly follows from (4.8). To prove (1.9), take an open subset W of
![]() $\mathbb{R}^n$
of the form
$\mathbb{R}^n$
of the form
![]() $I_1\times\cdots\times I_n$
, where
$I_1\times\cdots\times I_n$
, where
![]() $I_j$
are open intervals in
$I_j$
are open intervals in
![]() $\mathbb{R}$
, and suppose that
$\mathbb{R}$
, and suppose that
intersects with Y non-trivially, that is, we have
![]() $r\in Y_1$
. Then, again in view of (4.8), the union of subspaces
$r\in Y_1$
. Then, again in view of (4.8), the union of subspaces
![]() $A_j$
such that
$A_j$
such that
![]() $A_j\cap A \cap Y\cap W \ne\varnothing$
is dense in
$A_j\cap A \cap Y\cap W \ne\varnothing$
is dense in
![]() $(I_1\cap Y_1)\times\mathbb{R}\times \cdots\times \mathbb{R}$
, and hence the union of corresponding intersections
$(I_1\cap Y_1)\times\mathbb{R}\times \cdots\times \mathbb{R}$
, and hence the union of corresponding intersections
![]() $Y \cap A_j$
is dense in
$Y \cap A_j$
is dense in
![]() $Y\cap(I_1\times\mathbb{R}\times \cdots\times \mathbb{R})$
.
$Y\cap(I_1\times\mathbb{R}\times \cdots\times \mathbb{R})$
.
It remains to prove that the collection
![]() $\{ Y \cap A_i\}$
respects an arbitrary closed analytic submanifold R of
$\{ Y \cap A_i\}$
respects an arbitrary closed analytic submanifold R of
![]() $\mathbb{R}^n$
. Suppose that, for A as in (4.9), the intersection
$\mathbb{R}^n$
. Suppose that, for A as in (4.9), the intersection
![]() $Y\cap A \cap R$
has a non-empty interior in
$Y\cap A \cap R$
has a non-empty interior in
![]() $Y\cap A$
. Take a point
$Y\cap A$
. Take a point
![]() $\mathbf{x} = (x_1,\dots,x_n)$
in the interior of
$\mathbf{x} = (x_1,\dots,x_n)$
in the interior of
![]() $Y\cap A \cap R$
; then there exists a neighborhood W of
$Y\cap A \cap R$
; then there exists a neighborhood W of
![]() $\mathbf{x}$
in
$\mathbf{x}$
in
![]() $\mathbb{R}^n$
such that
$\mathbb{R}^n$
such that
![]() $Y\cap A \cap R$
contains
$Y\cap A \cap R$
contains
![]() $\big(\{x_1\} \times Y_2 \times \cdots \times Y_n\big)\cap W$
. Since each of the sets
$\big(\{x_1\} \times Y_2 \times \cdots \times Y_n\big)\cap W$
. Since each of the sets
![]() $Y_i$
is perfect, there are sequences in
$Y_i$
is perfect, there are sequences in
![]() $Y\cap A \cap R$
approaching
$Y\cap A \cap R$
approaching
![]() $\mathbf{x}$
from each coordinate direction. This makes it possible to determine all partial derivatives of all orders of any analytic function on A at
$\mathbf{x}$
from each coordinate direction. This makes it possible to determine all partial derivatives of all orders of any analytic function on A at
![]() $(x_1,\dots,x_n)$
by its values on
$(x_1,\dots,x_n)$
by its values on
![]() $Y\cap A \cap R$
. In particular, since R is a closed analytic manifold, it has to contain A, and hence it is respected by
$Y\cap A \cap R$
. In particular, since R is a closed analytic manifold, it has to contain A, and hence it is respected by
![]() $Y\cap A$
.
$Y\cap A$
.
Now we can conclude that Theorem 1.5 applies and implies the density of
![]() $Y\cap \operatorname{UA}_{1,n}(f) \smallsetminus \bigcup_{\ell\in\mathbb{N}} R_\ell$
for any countable set of proper closed analytic submanifolds
$Y\cap \operatorname{UA}_{1,n}(f) \smallsetminus \bigcup_{\ell\in\mathbb{N}} R_\ell$
for any countable set of proper closed analytic submanifolds
![]() $R_\ell$
of
$R_\ell$
of
![]() $\mathbb{R}^n$
. The uncountability follows as well, since the sets
$\mathbb{R}^n$
. The uncountability follows as well, since the sets
![]() $\{ Y \cap A_i\}$
have no isolated points.
$\{ Y \cap A_i\}$
have no isolated points.
Remark 4.5. Our arguments can be adapted to many other fractal sets. We sketch one more example involving a ‘rational Koch snowflake’ which can be treated by our method. To define it, let
![]() $\alpha, \beta, \gamma, \delta$
be positive rational numbers, where
$\alpha, \beta, \gamma, \delta$
be positive rational numbers, where
![]() $\alpha < \beta < \delta < 1$
, and let Y be the attractor of the iterated function system
$\alpha < \beta < \delta < 1$
, and let Y be the attractor of the iterated function system
![]() $\{\varphi_1,\varphi_2, \varphi_3, \varphi_4\}$
, where
$\{\varphi_1,\varphi_2, \varphi_3, \varphi_4\}$
, where
![]() $\varphi_i : \mathbb{R}^2 \to \mathbb{R}^2$
is the unique orientation-preserving contracting similarity map sending the points
$\varphi_i : \mathbb{R}^2 \to \mathbb{R}^2$
is the unique orientation-preserving contracting similarity map sending the points
![]() $\mathbf{x}_0 = (0,0)$
and
$\mathbf{x}_0 = (0,0)$
and
![]() $\mathbf{y}_0 = (1,0)$
, to the points
$\mathbf{y}_0 = (1,0)$
, to the points
![]() $\mathbf{x}_i, \mathbf{y}_i$
defined by
$\mathbf{x}_i, \mathbf{y}_i$
defined by
 \[\begin{split} \mathbf{x}_1 = (0,0), \ \ \ &\mathbf{y}_1 = ( \alpha, 0) \\ \mathbf{x}_2 = \mathbf{y}_1,{\kern.25pt} \ \ \ \ \ \ &\mathbf{y}_2 = ( \beta, \gamma) \\ \mathbf{x}_3 = \mathbf{y}_2,{\kern.25pt} \ \ \ \ \ \ &\mathbf{y}_3 = (\delta, 0) \\ \mathbf{x}_4 = \mathbf{y}_3,{\kern.25pt} \ \ \ \ \ \ &\mathbf{y}_4 = ( 1, 0). \end{split}\]
\[\begin{split} \mathbf{x}_1 = (0,0), \ \ \ &\mathbf{y}_1 = ( \alpha, 0) \\ \mathbf{x}_2 = \mathbf{y}_1,{\kern.25pt} \ \ \ \ \ \ &\mathbf{y}_2 = ( \beta, \gamma) \\ \mathbf{x}_3 = \mathbf{y}_2,{\kern.25pt} \ \ \ \ \ \ &\mathbf{y}_3 = (\delta, 0) \\ \mathbf{x}_4 = \mathbf{y}_3,{\kern.25pt} \ \ \ \ \ \ &\mathbf{y}_4 = ( 1, 0). \end{split}\]
Then Y is a topological curve (continuous image of a segment) of Hausdorff dimension greater than one. The usual version of the Koch snowflake has a similar description, with
![]() $\alpha = \frac13,\,\beta = \frac12,\, \gamma = \frac{\sqrt{3}}{6}, \delta = \frac23$
(see [Reference FalconerFal04, Figure 0.2]).
$\alpha = \frac13,\,\beta = \frac12,\, \gamma = \frac{\sqrt{3}}{6}, \delta = \frac23$
(see [Reference FalconerFal04, Figure 0.2]).
For our application, it is important to note that if
![]() $\theta$
is the slope of the line from
$\theta$
is the slope of the line from
![]() $\mathbf{x}_2$
to
$\mathbf{x}_2$
to
![]() $\mathbf{y}_2$
, then Y contains a dense collection of rational points
$\mathbf{y}_2$
, then Y contains a dense collection of rational points
![]() $Y_0$
, and the horizontal lines and lines of slope
$Y_0$
, and the horizontal lines and lines of slope
![]() $\theta$
through points of
$\theta$
through points of
![]() $Y_0$
intersect Y in an uncountable perfect set. This property makes it possible to repeat the proof of Theorem 5.2, taking the sets
$Y_0$
intersect Y in an uncountable perfect set. This property makes it possible to repeat the proof of Theorem 5.2, taking the sets
![]() $\{A_i\}$
to be the lines having these two slopes and passing through
$\{A_i\}$
to be the lines having these two slopes and passing through
![]() $Y_0$
.
$Y_0$
.
5. Vectors that are k-singular for all k
In this section we prove a strengthening of Theorem 1.11. To state it, let us consider a definition generalizing the notion of k-singular vectors. Namely, for a non-increasing
![]() $f:\mathbb{R}_{>0} \to \mathbb{R}_{>0}$
we say that
$f:\mathbb{R}_{>0} \to \mathbb{R}_{>0}$
we say that
![]() $\mathbf{x}\in\mathbb{R}^n$
is f-uniform of degree k if for any sufficiently large t there exists a polynomial
$\mathbf{x}\in\mathbb{R}^n$
is f-uniform of degree k if for any sufficiently large t there exists a polynomial
![]() $P \in \mathbb{Z}[X_1, \ldots, X_n]$
such that
$P \in \mathbb{Z}[X_1, \ldots, X_n]$
such that
![]() $\deg (P) \leqslant k, \ H(P) \leqslant t,$
and
$\deg (P) \leqslant k, \ H(P) \leqslant t,$
and
![]() $|P(\mathbf{x})| \leqslant f(t)$
. Clearly
$|P(\mathbf{x})| \leqslant f(t)$
. Clearly
![]() $\mathbf{x}$
, viewed as a row vector, is k-singular (as defined in § 1.6) if and only if it is
$\mathbf{x}$
, viewed as a row vector, is k-singular (as defined in § 1.6) if and only if it is
![]() $\varepsilon\phi_{N_k}$
-uniform of degree k, where
$\varepsilon\phi_{N_k}$
-uniform of degree k, where
![]() $N_k$
is as in (1.14). Also it is clear that k-algebraic vectors (again see § 1.6 for a definition) are f-uniform of degree k for any positive f.
$N_k$
is as in (1.14). Also it is clear that k-algebraic vectors (again see § 1.6 for a definition) are f-uniform of degree k for any positive f.
Let us say that a submanifold
![]() ${Y} \subset {\mathbb{R}^n}$
is transcendental if Y is not contained in an algebraic subvariety defined over
${Y} \subset {\mathbb{R}^n}$
is transcendental if Y is not contained in an algebraic subvariety defined over
![]() $\mathbb{Q}$
or, more concretely, if there is no nonzero polynomial in
$\mathbb{Q}$
or, more concretely, if there is no nonzero polynomial in
![]() $\mathbb{Z}[X_1, \ldots, X_n]$
which vanishes on Y.
$\mathbb{Z}[X_1, \ldots, X_n]$
which vanishes on Y.
Theorem 5.1. Let
![]() $n \geqslant 2$
, and let Y be a transcendental analytic submanifold of
$n \geqslant 2$
, and let Y be a transcendental analytic submanifold of
![]() $\mathbb{R}^n$
of dimension
$\mathbb{R}^n$
of dimension
![]() $d\geqslant 2$
. Suppose that for each
$d\geqslant 2$
. Suppose that for each
![]() $k\in\mathbb{N}$
we are given a non-increasing
$k\in\mathbb{N}$
we are given a non-increasing
![]() $f_k:\mathbb{R}_{>0} \to \mathbb{R}_{>0}$
. Then there is a dense uncountable set of
$f_k:\mathbb{R}_{>0} \to \mathbb{R}_{>0}$
. Then there is a dense uncountable set of
![]() $\mathbf{x} \in {Y}$
which are not algebraic and are
$\mathbf{x} \in {Y}$
which are not algebraic and are
![]() $f_k$
-uniform of degree k for all
$f_k$
-uniform of degree k for all
![]() $k \in \mathbb{N}$
. In particular, Y contains a dense uncountable set of
$k \in \mathbb{N}$
. In particular, Y contains a dense uncountable set of
![]() $\mathbf{x} $
which are not algebraic and are k-singular for all
$\mathbf{x} $
which are not algebraic and are k-singular for all
![]() $k \in \mathbb{N}$
.
$k \in \mathbb{N}$
.
This result extends [Reference Kleinbock, Moshchevitin and WeissKMW21, Theorem 1.7]; namely, there it was shown that Y as above contains uncountably many singular vectors.
The proof is based on the following observation. For
![]() $\mathbf{x} \in \mathbb{R}^n$
, denote by
$\mathbf{x} \in \mathbb{R}^n$
, denote by
![]() $\varphi_k(\mathbf{x})$
the vector with coordinates consisting of all non-constant monomials of degree at most k in n variables
$\varphi_k(\mathbf{x})$
the vector with coordinates consisting of all non-constant monomials of degree at most k in n variables
![]() $x_1,\dots,x_n$
, viewed as a row vector in
$x_1,\dots,x_n$
, viewed as a row vector in
![]() $\mathbb{R}^{N(k,n)}$
, and for each k consider the standard Diophantine system
$\mathbb{R}^{N(k,n)}$
, and for each k consider the standard Diophantine system
![]() $\mathcal{X}_{1,N(k,n)}$
on
$\mathcal{X}_{1,N(k,n)}$
on
![]() $X_k = \mathbb{R}^{N(k,n)}\cong M_{1,N(k,n)}$
with distance functions from rational affine hyperplanes and standard heights. Then it is clear that
$X_k = \mathbb{R}^{N(k,n)}\cong M_{1,N(k,n)}$
with distance functions from rational affine hyperplanes and standard heights. Then it is clear that
![]() $\mathbf{x} \in \mathbb{R}^n$
is
$\mathbf{x} \in \mathbb{R}^n$
is
![]() $f_k$
-uniform of degree k if and only if
$f_k$
-uniform of degree k if and only if
![]() $\varphi_k(\mathbf{x}) \in \operatorname{UA}_{1,N(k,n)}(f_k)$
. The proof is as follows.
$\varphi_k(\mathbf{x}) \in \operatorname{UA}_{1,N(k,n)}(f_k)$
. The proof is as follows.
Proof of Theorem 5.1. Take Y as in the statement of Theorem 5.1 and argue as in the proof of Theorem 4.2. Namely, for any
![]() $\mathbf{y}\in Y$
define:
$\mathbf{y}\in Y$
define:
-
• a neighborhood W of
 $\mathbf{y}$
such that
$\mathbf{y}$
such that
 $Y\cap W$
is a graph of an analytic function
$Y\cap W$
is a graph of an analytic function
 $\mathbb{R}^d\to \mathbb{R}^{n-d}$
; and
$\mathbb{R}^d\to \mathbb{R}^{n-d}$
; and -
• (using Lemma 4.3 with
 $g=1$
) a totally dense collection
$g=1$
) a totally dense collection
 $\mathcal{L}_W$
of intersections of some rational affine hyperplanes of
$\mathcal{L}_W$
of intersections of some rational affine hyperplanes of
 $\mathbb{R}^n$
with
$\mathbb{R}^n$
with
 $Y\cap W$
.
$Y\cap W$
.
It is clear that
![]() $\mathcal{L}_W$
as above is aligned with
$\mathcal{L}_W$
as above is aligned with
![]() $\mathcal{X}_{1,N(k,n)}$
via
$\mathcal{X}_{1,N(k,n)}$
via
![]() $\varphi_k$
: indeed, if
$\varphi_k$
: indeed, if
![]() $\pi: \mathbb{R}^{N(k,n)} \to \mathbb{R}^n$
denotes the projection onto the first n coordinates and L is a rational affine hyperplane in
$\pi: \mathbb{R}^{N(k,n)} \to \mathbb{R}^n$
denotes the projection onto the first n coordinates and L is a rational affine hyperplane in
![]() $\mathbb{R}^n$
, then
$\mathbb{R}^n$
, then
![]() $\varphi_k(L)$
is contained in
$\varphi_k(L)$
is contained in
![]() $\pi^{-1}(L)$
, which is a rational affine hyperplane in
$\pi^{-1}(L)$
, which is a rational affine hyperplane in
![]() $ \mathbb{R}^{N(k,n)}$
. Now let
$ \mathbb{R}^{N(k,n)}$
. Now let
![]() $\{R_\ell\}$
be the collection of sets of the form
$\{R_\ell\}$
be the collection of sets of the form
![]() $\{\mathbf{y} \in Y: P(\mathbf{y}) =0\}$
, where P ranges over all nonzero polynomials in
$\{\mathbf{y} \in Y: P(\mathbf{y}) =0\}$
, where P ranges over all nonzero polynomials in
![]() $\mathbb{Z}[X_1, \ldots, X_n]$
. Since Y is assumed to be transcendental, it follows that each of the sets
$\mathbb{Z}[X_1, \ldots, X_n]$
. Since Y is assumed to be transcendental, it follows that each of the sets
![]() $R_\ell$
is a proper subset of Y. It is easy to show that
$R_\ell$
is a proper subset of Y. It is easy to show that
![]() $\mathcal{L}_W$
respects
$\mathcal{L}_W$
respects
![]() $R_\ell$
: indeed, any element L of
$R_\ell$
: indeed, any element L of
![]() $\mathcal{L}_W$
is of the form (4.7) with analytic
$\mathcal{L}_W$
is of the form (4.7) with analytic
![]() ${\psi}$
; furthermore, the fact that
${\psi}$
; furthermore, the fact that
![]() $L\cap R_\ell$
has non-empty interior in L implies that
$L\cap R_\ell$
has non-empty interior in L implies that
![]() $P\big(x_1, \dots,x_d, \psi(x_1, \dots,x_d)\big) = 0$
on an open subset of an affine hyperplane M of
$P\big(x_1, \dots,x_d, \psi(x_1, \dots,x_d)\big) = 0$
on an open subset of an affine hyperplane M of
![]() $\mathbb{R}^d$
. Since
$\mathbb{R}^d$
. Since
![]() $d\geqslant 2$
and
$d\geqslant 2$
and
![]() ${\psi}$
is analytic, it follows that
${\psi}$
is analytic, it follows that
![]() $L\subset R_\ell$
. Hence Theorem 5 applies, and we conclude that the set
$L\subset R_\ell$
. Hence Theorem 5 applies, and we conclude that the set
which contains the set of vectors that are not algebraic and are
![]() $f_k$
-uniform of degree k for all
$f_k$
-uniform of degree k for all
![]() $k \in \mathbb{N}$
, is uncountable and dense in Y for any choice of non-increasing functions
$k \in \mathbb{N}$
, is uncountable and dense in Y for any choice of non-increasing functions
![]() $f_k: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
.
$f_k: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
.
Using similar ideas and arguing as in the proof of Theorem 4.4 and Remark 4.5, one can establish a similar result for fractals.
6. Sumsets of sets of totally irrational uniformly approximable vectors
Our goal in this section is to prove Theorem 1.12, which states that when
![]() $n\geqslant 3$
, the sum of
$n\geqslant 3$
, the sum of
![]() $\operatorname{UA}^*_{1,n}(f_1) $
and
$\operatorname{UA}^*_{1,n}(f_1) $
and
![]() $\operatorname{UA}^*_{1,n}(f_2) $
is
$\operatorname{UA}^*_{1,n}(f_2) $
is
![]() $\mathbb{R}^n$
for any pair of approximating functions
$\mathbb{R}^n$
for any pair of approximating functions
![]() $f_1,f_2$
. Clearly, by replacing each of the functions
$f_1,f_2$
. Clearly, by replacing each of the functions
![]() $f_i$
with
$f_i$
with
![]() $\min(f_1,f_2)$
, it is enough to take a non-increasing
$\min(f_1,f_2)$
, it is enough to take a non-increasing
![]() $f:\mathbb{R}_{>0}\to \mathbb{R}_{>0}$
and prove that
$f:\mathbb{R}_{>0}\to \mathbb{R}_{>0}$
and prove that
![]() $\operatorname{UA}^*_{1,n}(f) +\operatorname{UA}^*_{1,n}(f) =\mathbb{R}^n$
. Equivalently, since
$\operatorname{UA}^*_{1,n}(f) +\operatorname{UA}^*_{1,n}(f) =\mathbb{R}^n$
. Equivalently, since
![]() $\operatorname{UA}^*_{1,n}(f) $
coincides with
$\operatorname{UA}^*_{1,n}(f) $
coincides with
![]() $ -\operatorname{UA}^*_{1,n}(f)$
, we need to show that for any fixed
$ -\operatorname{UA}^*_{1,n}(f)$
, we need to show that for any fixed
![]() $\mathbf{z} \in \mathbb{R}^n$
the intersection of
$\mathbf{z} \in \mathbb{R}^n$
the intersection of
![]() $\operatorname{UA}^* _{1,n}(f) $
and its translate
$\operatorname{UA}^* _{1,n}(f) $
and its translate
![]() $\operatorname{UA}^*_{1,n}(f) - \mathbf{z}$
is not empty. Unwrapping the definitions, we see that this amounts to finding
$\operatorname{UA}^*_{1,n}(f) - \mathbf{z}$
is not empty. Unwrapping the definitions, we see that this amounts to finding
![]() $\mathbf{x}\in\mathbb{R}^n$
such that both
$\mathbf{x}\in\mathbb{R}^n$
such that both
![]() $\mathbf{x}$
and
$\mathbf{x}$
and
![]() $\mathbf{x} +\mathbf{z}$
are totally irrational and such that for every sufficiently large t one can find
$\mathbf{x} +\mathbf{z}$
are totally irrational and such that for every sufficiently large t one can find
![]() $\textbf{q} \in \mathbb{Z}^n\smallsetminus\{0\}$
and
$\textbf{q} \in \mathbb{Z}^n\smallsetminus\{0\}$
and
![]() $p \in \mathbb{Z}$
with
$p \in \mathbb{Z}$
with
and also
![]() $\textbf{q}' \in \mathbb{Z}^n\smallsetminus\{0\}$
and
$\textbf{q}' \in \mathbb{Z}^n\smallsetminus\{0\}$
and
![]() $p' \in \mathbb{Z}$
with
$p' \in \mathbb{Z}$
with
Rewriting the two systems of inequalities above as
we see that the problem reduces to a new Diophantine system
where
![]() $d_{p,p',\textbf{q},\textbf{q}'}(\mathbf{x}) := \max(|\mathbf{x}\cdot\textbf{q} -p|,|(\mathbf{x}-\mathbf{z})\cdot\textbf{q}' -p'|)$
,
$d_{p,p',\textbf{q},\textbf{q}'}(\mathbf{x}) := \max(|\mathbf{x}\cdot\textbf{q} -p|,|(\mathbf{x}-\mathbf{z})\cdot\textbf{q}' -p'|)$
,
![]() $h_{p,p',\textbf{q},\textbf{q}'} := \max(\|\textbf{q}\|,\|\textbf{q}'\|)$
, and
$h_{p,p',\textbf{q},\textbf{q}'} := \max(\|\textbf{q}\|,\|\textbf{q}'\|)$
, and
![]() $(p,p', \textbf{q},\textbf{q}')$
runs through
$(p,p', \textbf{q},\textbf{q}')$
runs through
![]() $\mathbb{Z}\times \mathbb{Z}\times (\mathbb{Z}^n\smallsetminus\{0\})\times(\mathbb{Z}^n\smallsetminus\{0\})$
. Note that the zero locus of
$\mathbb{Z}\times \mathbb{Z}\times (\mathbb{Z}^n\smallsetminus\{0\})\times(\mathbb{Z}^n\smallsetminus\{0\})$
. Note that the zero locus of
![]() $d_{p,p',\textbf{q},\textbf{q}'}$
is precisely the intersection
$d_{p,p',\textbf{q},\textbf{q}'}$
is precisely the intersection
![]() $L_{p, \textbf{q}} \cap (L_{p', \textbf{q}'} + \mathbf{z})$
of two hyperplanes in
$L_{p, \textbf{q}} \cap (L_{p', \textbf{q}'} + \mathbf{z})$
of two hyperplanes in
![]() $\mathbb{R}^n$
; in other words, the collection
$\mathbb{R}^n$
; in other words, the collection
is aligned with the Diophantine system
![]() ${\mathcal{X}_\mathbf{z}}$
. The crucial step of the proof of Theorem 1.12 will be the following lemma.
${\mathcal{X}_\mathbf{z}}$
. The crucial step of the proof of Theorem 1.12 will be the following lemma.
Lemma 6.1. Let
![]() $n \geqslant 3$
and
$n \geqslant 3$
and
![]() $\mathbf{z}\in\mathbb{R}^n$
. Then
$\mathbf{z}\in\mathbb{R}^n$
. Then
![]() $\mathcal{L}_\mathbf{z}$
is totally dense relative to the collection of all affine hyperplanes in
$\mathcal{L}_\mathbf{z}$
is totally dense relative to the collection of all affine hyperplanes in
![]() $\mathbb{R}^n$
.
$\mathbb{R}^n$
.
Note that we are not able to prove the stronger form of total density, that is, the validity of (1.9) for
![]() $\mathcal{L} = \mathcal{L}_\mathbf{z}$
.
$\mathcal{L} = \mathcal{L}_\mathbf{z}$
.
Proof of Lemma 6.1. Let us start with the following elementary sublemma.
Sublemma 6.2. Let
![]() $n \geqslant 3$
and let N be an affine hyperplane of
$n \geqslant 3$
and let N be an affine hyperplane of
![]() $\mathbb{R}^n$
. Then the collection
$\mathbb{R}^n$
. Then the collection
is totally dense in N; furthermore, the union in (1.9) is dense in N.
Proof. By permuting coordinates, without loss of generality we can express N in the form
in this way the projection
![]() $\pi:(x_1,\dots,x_n)\mapsto(x_1,\dots,x_{n-1})$
maps N bijectively onto
$\pi:(x_1,\dots,x_n)\mapsto(x_1,\dots,x_{n-1})$
maps N bijectively onto
![]() $\mathbb{R}^{n-1}$
. Furthermore, any
$\mathbb{R}^{n-1}$
. Furthermore, any
![]() $L\in \mathcal{L}(N)$
is of the form
$L\in \mathcal{L}(N)$
is of the form
for some
![]() $\mathbf{q}\in\mathbb{Z}^n\smallsetminus\{0\}$
and
$\mathbf{q}\in\mathbb{Z}^n\smallsetminus\{0\}$
and
![]() $p\in\mathbb{Z}$
. It suffices to prove that the collection
$p\in\mathbb{Z}$
. It suffices to prove that the collection
![]() $\pi\big(\mathcal{L}(N)\big)$
of affine hyperplanes of
$\pi\big(\mathcal{L}(N)\big)$
of affine hyperplanes of
![]() $\mathbb{R}^{n-1}$
is totally dense in
$\mathbb{R}^{n-1}$
is totally dense in
![]() $\mathbb{R}^{n-1}$
. By considering the case
$\mathbb{R}^{n-1}$
. By considering the case
![]() $q_n = 0$
in (6.1), it is easy to see that
$q_n = 0$
in (6.1), it is easy to see that
![]() $\pi\big(\mathcal{L}(N)\big)$
contains the collection of all rational affine hyperplanes of
$\pi\big(\mathcal{L}(N)\big)$
contains the collection of all rational affine hyperplanes of
![]() $\mathbb{R}^{n-1}$
. The latter collection, in additional to being totally dense, has the following property: for any affine hyperplane L of
$\mathbb{R}^{n-1}$
. The latter collection, in additional to being totally dense, has the following property: for any affine hyperplane L of
![]() $\mathbb{R}^{n-1}$
, any open
$\mathbb{R}^{n-1}$
, any open
![]() $W\subset \mathbb{R}^{n-1}$
with
$W\subset \mathbb{R}^{n-1}$
with
![]() $W\cap L \ne\varnothing$
and any
$W\cap L \ne\varnothing$
and any
![]() $\mathbf{y}\in\mathbb{Q}^{n-1}\smallsetminus L$
there exists
$\mathbf{y}\in\mathbb{Q}^{n-1}\smallsetminus L$
there exists
![]() $\mathbf{y}'\in\mathbb{Q}^{n-1}$
such that the (rational) line passing through
$\mathbf{y}'\in\mathbb{Q}^{n-1}$
such that the (rational) line passing through
![]() $\mathbf{y}$
and
$\mathbf{y}$
and
![]() $\mathbf{y}'$
intersects
$\mathbf{y}'$
intersects
![]() $W\cap L$
. This clearly implies that the union of all rational affine hyperplanes touching
$W\cap L$
. This clearly implies that the union of all rational affine hyperplanes touching
![]() $W\cap L \ne\varnothing$
is dense in
$W\cap L \ne\varnothing$
is dense in
![]() $\mathbb{R}^{n-1}$
, and hence the total density of
$\mathbb{R}^{n-1}$
, and hence the total density of
![]() $\pi\big(\mathcal{L}(N)\big)$
.
$\pi\big(\mathcal{L}(N)\big)$
.
The above sublemma implies, in particular, that for any
![]() $N = L_{p', \textbf{q}'} + \mathbf{z}$
the union
$N = L_{p', \textbf{q}'} + \mathbf{z}$
the union
is dense in N. Since the union of all rational affine hyperplanes translated by
![]() $\mathbf{z}$
is dense in
$\mathbf{z}$
is dense in
![]() $\mathbb{R}^n$
, it follows that
$\mathbb{R}^n$
, it follows that
![]() $\bigcup_{L\in{\mathcal L}_\mathbf{z}}L$
is dense in
$\bigcup_{L\in{\mathcal L}_\mathbf{z}}L$
is dense in
![]() $\mathbb{R}^n$
, i.e. condition (1.7) holds.
$\mathbb{R}^n$
, i.e. condition (1.7) holds.
Now take
![]() $L\in{\mathcal L}_\mathbf{z}$
, that is,
$L\in{\mathcal L}_\mathbf{z}$
, that is,
![]() $L = L_{p, \textbf{q}} \cap (L_{p', \textbf{q}'} + \mathbf{z}) $
such that
$L = L_{p, \textbf{q}} \cap (L_{p', \textbf{q}'} + \mathbf{z}) $
such that
![]() $ \textbf{q}$
and
$ \textbf{q}$
and
![]() $\textbf{q}'$
are not proportional, and choose an open subset W of
$\textbf{q}'$
are not proportional, and choose an open subset W of
![]() $\mathbb{R}^n$
with
$\mathbb{R}^n$
with
![]() $L\cap W\ne\varnothing$
. For brevity we write
$L\cap W\ne\varnothing$
. For brevity we write
![]() $M {\, \stackrel{\mathrm{def}}{=}\, } L_{p, \textbf{q}}$
and
$M {\, \stackrel{\mathrm{def}}{=}\, } L_{p, \textbf{q}}$
and
![]() ${N} {\, \stackrel{\mathrm{def}}{=}\, } L_{p', \textbf{q}'} + \mathbf{z}$
. It follows from Sublemma 6.2 that the union of
${N} {\, \stackrel{\mathrm{def}}{=}\, } L_{p', \textbf{q}'} + \mathbf{z}$
. It follows from Sublemma 6.2 that the union of
![]() $P\cap N$
over all rational affine hyperplanes
$P\cap N$
over all rational affine hyperplanes
![]() $P\ne N$
that satisfy
$P\ne N$
that satisfy
![]() $P\cap W\cap L\ne\varnothing$
is dense in N. Applying a translation by
$P\cap W\cap L\ne\varnothing$
is dense in N. Applying a translation by
![]() $-\mathbf{z}$
to the above conclusion one gets that the union of
$-\mathbf{z}$
to the above conclusion one gets that the union of
![]() $(P+\mathbf{z})\cap M$
over all rational affine hyperplanes P with
$(P+\mathbf{z})\cap M$
over all rational affine hyperplanes P with
![]() $P+\mathbf{z} \ne M$
and
$P+\mathbf{z} \ne M$
and
![]() $P\cap W\cap L\ne\varnothing$
is dense in M. It follows that the closure of the union of all
$P\cap W\cap L\ne\varnothing$
is dense in M. It follows that the closure of the union of all
![]() $L'\in{\mathcal L}_\mathbf{z}$
such that
$L'\in{\mathcal L}_\mathbf{z}$
such that
![]() $L'\cap W\cap L\ne\varnothing$
contains
$L'\cap W\cap L\ne\varnothing$
contains
![]() $M\cup N$
, and thus it cannot be a subset of a single affine hyperplane.
$M\cup N$
, and thus it cannot be a subset of a single affine hyperplane.
Now, since
![]() $\mathcal{L}_\mathbf{z}$
obviously respects any affine subspace in
$\mathcal{L}_\mathbf{z}$
obviously respects any affine subspace in
![]() $\mathbb{R}^n$
, we can apply Theorem 1.5 to
$\mathbb{R}^n$
, we can apply Theorem 1.5 to
![]() $\mathcal X_\mathbf{z}$
with
$\mathcal X_\mathbf{z}$
with
![]() $\mathcal{R} = \{R_\ell\}$
being an arbitrary countable collection of affine hyperplanes of
$\mathcal{R} = \{R_\ell\}$
being an arbitrary countable collection of affine hyperplanes of
![]() $\mathbb{R}^n$
. This immediately yields the proof of Theorem 1.12 in a slightly more general form, with
$\mathbb{R}^n$
. This immediately yields the proof of Theorem 1.12 in a slightly more general form, with
![]() $\operatorname{UA}^*_{1,n}(f_k)$
,
$\operatorname{UA}^*_{1,n}(f_k)$
,
![]() $k=1,2$
, in (1.15) replaced by
$k=1,2$
, in (1.15) replaced by
![]() $\operatorname{UA}_{1,n}(f_k) \smallsetminus\bigcup_\ell R_\ell$
for
$\operatorname{UA}_{1,n}(f_k) \smallsetminus\bigcup_\ell R_\ell$
for
![]() $\mathcal{R}$
as above.
$\mathcal{R}$
as above.
Remark 6.3. It is not hard to show, by adapting the above proof, that for any
![]() $n \geqslant 3$
, any positive non-increasing
$n \geqslant 3$
, any positive non-increasing
![]() $f_1, \ldots, f_{n-1}$
, and any
$f_1, \ldots, f_{n-1}$
, and any
![]() $\mathbf{z}_1,\ldots, \mathbf{z}_{n-1}$
, we have
$\mathbf{z}_1,\ldots, \mathbf{z}_{n-1}$
, we have
 $$\bigcap_{k=1}^{n-1}( \operatorname{UA}^*_{1,n}(f_k) - \mathbf{z}_k) \neq \varnothing.$$
$$\bigcap_{k=1}^{n-1}( \operatorname{UA}^*_{1,n}(f_k) - \mathbf{z}_k) \neq \varnothing.$$
Note that our method gives no information on the intersection of translates of
![]() $\operatorname{UA}^*_{1,2}(f)$
. In particular, it is an open problem to determine whether for any non-increasing
$\operatorname{UA}^*_{1,2}(f)$
. In particular, it is an open problem to determine whether for any non-increasing
![]() $f:\mathbb{R}_{>0}\to \mathbb{R}_{>0}$
the sumset of
$f:\mathbb{R}_{>0}\to \mathbb{R}_{>0}$
the sumset of
![]() $\operatorname{UA}^*_{1,2}(f)$
with itself coincides with
$\operatorname{UA}^*_{1,2}(f)$
with itself coincides with
![]() $\mathbb{R}^2$
.
$\mathbb{R}^2$
.
7. Transference and improved rates for vectors in analytic submanifolds of
 $\mathbb{R}^n$
$\mathbb{R}^n$
Given
![]() $\mathbf{x} = (x_1, \ldots, x_n)\in\mathbb{R}^n$
and real numbers
$\mathbf{x} = (x_1, \ldots, x_n)\in\mathbb{R}^n$
and real numbers
![]() $\tau, \varepsilon, t, \eta$
, define the following parallelepipeds:
$\tau, \varepsilon, t, \eta$
, define the following parallelepipeds:
and
Note that
![]() $\Pi^{\tau, \varepsilon}$
encodes information about approximations to
$\Pi^{\tau, \varepsilon}$
encodes information about approximations to
![]() $\mathbf{x}$
as a linear form, while
$\mathbf{x}$
as a linear form, while
![]() $\Pi_{t, \eta}$
encodes approximations to
$\Pi_{t, \eta}$
encodes approximations to
![]() $\mathbf{x}$
as a vector.
$\mathbf{x}$
as a vector.
With these definitions, we have the following standard transference result:
Lemma 7.1. Let
![]() $1\leqslant g \leqslant n$
, suppose that
$1\leqslant g \leqslant n$
, suppose that
![]() $\tau, \varepsilon, t, \eta$
satisfy
$\tau, \varepsilon, t, \eta$
satisfy
and
and assume that the parallelepiped
![]() $\Pi^{\tau,\varepsilon} $
contains g linearly independent integer points. Then
$\Pi^{\tau,\varepsilon} $
contains g linearly independent integer points. Then
![]() $\Pi_{t, \eta}$
contains a nonzero integer point.
$\Pi_{t, \eta}$
contains a nonzero integer point.
Proof. Let
![]() $ \mathbf{z}_1, \ldots ,\mathbf{z}_g$
be linearly independent integer points in
$ \mathbf{z}_1, \ldots ,\mathbf{z}_g$
be linearly independent integer points in
![]() $\Pi^{\tau, \varepsilon}$
, let
$\Pi^{\tau, \varepsilon}$
, let
be the space generated by these points, and denote the orthogonal complement of L by
![]() ${L}^\perp$
. Clearly
${L}^\perp$
. Clearly
![]() $\Lambda {\, \stackrel{\mathrm{def}}{=}\, } {L}\cap\mathbb{Z}^{n+1}$
is a lattice in L, and since
$\Lambda {\, \stackrel{\mathrm{def}}{=}\, } {L}\cap\mathbb{Z}^{n+1}$
is a lattice in L, and since
![]() ${L}^\perp$
is rational,
${L}^\perp$
is rational,
![]() $\Lambda^\perp = {L}^\perp\cap\mathbb{Z}^{n+1}$
is a lattice in
$\Lambda^\perp = {L}^\perp\cap\mathbb{Z}^{n+1}$
is a lattice in
![]() ${L}^\perp.$
It is well known that the covolumes
${L}^\perp.$
It is well known that the covolumes
![]() $\mathrm{covol}({L}/\Lambda)$
and
$\mathrm{covol}({L}/\Lambda)$
and
![]() $\mathrm{covol}({L}^\perp/\Lambda^\perp)$
are equal to each other. Now define
$\mathrm{covol}({L}^\perp/\Lambda^\perp)$
are equal to each other. Now define
![]() $ \Omega {\, \stackrel{\mathrm{def}}{=}\, } {L} \cap \Pi^{\tau, \varepsilon}$
and
$ \Omega {\, \stackrel{\mathrm{def}}{=}\, } {L} \cap \Pi^{\tau, \varepsilon}$
and
![]() $ \Omega^\perp {\, \stackrel{\mathrm{def}}{=}\, } {L}^\perp \cap \Pi_{t, \eta}$
, and denote by
$ \Omega^\perp {\, \stackrel{\mathrm{def}}{=}\, } {L}^\perp \cap \Pi_{t, \eta}$
, and denote by
![]() ${\rm vol}_g \Omega$
and
${\rm vol}_g \Omega$
and
![]() ${\rm vol}_{n+1-g} \Omega^\perp$
, respectively, the g-dimensional and
${\rm vol}_{n+1-g} \Omega^\perp$
, respectively, the g-dimensional and
![]() $(n-g+1)$
-dimensional volumes of
$(n-g+1)$
-dimensional volumes of
![]() $\Omega$
and
$\Omega$
and
![]() $\Omega^\perp$
.
$\Omega^\perp$
.
Denote the vector
![]() $(1,x_1,\dots,x_n)\in\mathbb{R}^{n+1}$
by
$(1,x_1,\dots,x_n)\in\mathbb{R}^{n+1}$
by
![]() $\mathbf{x}_0$
, and let
$\mathbf{x}_0$
, and let
be the hyperplane orthogonal to
![]() $\mathbf{x}_0$
. Let us define
$\mathbf{x}_0$
. Let us define
to be the maximal angle between vectors in L and M, and
It is easy to see that
![]() $\theta_{\min}\leqslant \theta_{\max}$
. Indeed, let
$\theta_{\min}\leqslant \theta_{\max}$
. Indeed, let
![]() $\mathbf{u}_0$
be the minimizer in the definition of
$\mathbf{u}_0$
be the minimizer in the definition of
![]() $\theta_{\min}$
, let V be the two-dimensional subspace generated by
$\theta_{\min}$
, let V be the two-dimensional subspace generated by
![]() $\mathbf{x}_0$
and
$\mathbf{x}_0$
and
![]() $\mathbf{u}_0$
, and let
$\mathbf{u}_0$
, and let
![]() $\mathbf{u}_0^\perp$
and
$\mathbf{u}_0^\perp$
and
![]() $\mathbf{x}_0^\perp$
be unit vectors in V perpendicular to
$\mathbf{x}_0^\perp$
be unit vectors in V perpendicular to
![]() $\mathbf{u}_0$
and
$\mathbf{u}_0$
and
![]() $\mathbf{x}_0$
respectively. Then
$\mathbf{x}_0$
respectively. Then
Let us now consider two cases. Suppose that
![]() $\sin \theta_{\min} \leqslant \frac{\eta}{t}$
. Then we have a lower bound
$\sin \theta_{\min} \leqslant \frac{\eta}{t}$
. Then we have a lower bound
and an upper bound
Note that
![]() $\Omega$
contains the convex hull of
$\Omega$
contains the convex hull of
![]() $\{\pm \mathbf{z}_1,\ldots, \pm \mathbf{z}_g\}$
, and the parallelepiped
$\{\pm \mathbf{z}_1,\ldots, \pm \mathbf{z}_g\}$
, and the parallelepiped
contains a fundamental domain for
![]() $\Lambda$
. Therefore we have
$\Lambda$
. Therefore we have

By the Minkowski Convex Body Theorem there exists a nonzero integer point in
![]() $\Omega^\perp \subset \Pi_{t, \eta}$
. Hence we are done in this case.
$\Omega^\perp \subset \Pi_{t, \eta}$
. Hence we are done in this case.
Now suppose that
![]() $\sin \theta_{\min} > {\eta}/{t}$
. Then
$\sin \theta_{\min} > {\eta}/{t}$
. Then
and
Arguing as in the previous case but using (7.5) and (7.6) instead of (7.3) and (7.4), we obtain

and, again by the Minkowski Convex Body Theorem, we get a nonzero integer point in
![]() $\Omega^\perp \subset \Pi_{t, \eta}$
.
$\Omega^\perp \subset \Pi_{t, \eta}$
.
Now let us state and prove a generalization of Theorem 1.13.
Theorem 7.2. Let
![]() $n\geqslant 2$
, let Y be a d-dimensional connected analytic submanifold of
$n\geqslant 2$
, let Y be a d-dimensional connected analytic submanifold of
![]() $\mathbb{R}^n\cong M_{n,1}(\mathbb{R})$
, where
$\mathbb{R}^n\cong M_{n,1}(\mathbb{R})$
, where
![]() $d\geqslant 2$
, and let
$d\geqslant 2$
, and let
![]() $\{R_\ell \}$
be a countable collection of proper closed analytic submanifolds of Y. Suppose that a continuous non-decreasing function f satisfies (1.17). Then the set
$\{R_\ell \}$
be a countable collection of proper closed analytic submanifolds of Y. Suppose that a continuous non-decreasing function f satisfies (1.17). Then the set
is uncountable and dense in Y-2pt. In particular, if one in addition assumes that Y is not contained in any proper rational affine subspace of
![]() $\mathbb{R}^n$
, then the set
$\mathbb{R}^n$
, then the set
![]() $Y\cap \operatorname{UA}^*_{n,1}(f) % \smallsetminus \bigcup % _{\ell\in\N} R_\ell $
is uncountable and dense in Y-2pt.
$Y\cap \operatorname{UA}^*_{n,1}(f) % \smallsetminus \bigcup % _{\ell\in\N} R_\ell $
is uncountable and dense in Y-2pt.
Proof. For
![]() $t> 0$
and
$t> 0$
and
![]() $g {\, \stackrel{\mathrm{def}}{=}\, } d-1$
, let us set
$g {\, \stackrel{\mathrm{def}}{=}\, } d-1$
, let us set
![]() $\eta {\, \stackrel{\mathrm{def}}{=}\, } f (t)$
and
$\eta {\, \stackrel{\mathrm{def}}{=}\, } f (t)$
and
![]() $\tau {\, \stackrel{\mathrm{def}}{=}\, } ({(\eta^{n-g}t)}/{ {(4n)^{2n}}})^{1/g}, $
so that (7.2) is satisfied, and the function
$\tau {\, \stackrel{\mathrm{def}}{=}\, } ({(\eta^{n-g}t)}/{ {(4n)^{2n}}})^{1/g}, $
so that (7.2) is satisfied, and the function
![]() $t\mapsto \tau$
is continuous. By (1.17), we have that
$t\mapsto \tau$
is continuous. By (1.17), we have that
![]() $ \tau \to \infty$
monotonically when
$ \tau \to \infty$
monotonically when
![]() $t\to \infty$
. The map
$t\to \infty$
. The map
![]() $t \mapsto \tau$
is thus bijective, and hence one can consider the inverse map
$t \mapsto \tau$
is thus bijective, and hence one can consider the inverse map
![]() $ \tau\mapsto t(\tau)$
and define a positive function
$ \tau\mapsto t(\tau)$
and define a positive function
so that (7.1) holds. Note that h is non-increasing, since so is the function
 $$h\big(\tau(t)\big) = \frac{( {f(t)^{n-g}t}/{ {(4n)^{2n}}} )^{1/g}f(t)}t = \frac{f(t)^{n/g}}{ {(4n)}^{2n/g}t^{1-1/g}}.$$
$$h\big(\tau(t)\big) = \frac{( {f(t)^{n-g}t}/{ {(4n)^{2n}}} )^{1/g}f(t)}t = \frac{f(t)^{n/g}}{ {(4n)}^{2n/g}t^{1-1/g}}.$$
We will prove the implication
This, in view of Theorem 4.2, will immediately imply the conclusion of Theorem 7.2.
To prove (7.7), note that
![]() $\mathbf{x}^T\in \operatorname{UA}_{1,n}(h;g)$
amounts to saying that for any large enough
$\mathbf{x}^T\in \operatorname{UA}_{1,n}(h;g)$
amounts to saying that for any large enough
![]() $\tau$
the parallelepiped
$\tau$
the parallelepiped
![]() $\Pi^{\tau,\varepsilon}$
contains g linearly independent integer points. In view of Lemma 7.1 we get that for all t large enough, the parallelepiped
$\Pi^{\tau,\varepsilon}$
contains g linearly independent integer points. In view of Lemma 7.1 we get that for all t large enough, the parallelepiped
![]() $\Pi_{t, \eta}$
contains a nonzero integer point
$\Pi_{t, \eta}$
contains a nonzero integer point
![]() $\mathbf{z} =(q, \mathbf{p})$
. For t large enough, the first coordinate q will be nonzero; thus we can find
$\mathbf{z} =(q, \mathbf{p})$
. For t large enough, the first coordinate q will be nonzero; thus we can find
![]() $q \in \mathbb{Z}\smallsetminus\{0\}$
and
$q \in \mathbb{Z}\smallsetminus\{0\}$
and
![]() $\mathbf{p} \in \mathbb{Z}^n$
such that
$\mathbf{p} \in \mathbb{Z}^n$
such that
![]() $q \leqslant t$
and
$q \leqslant t$
and
![]() $\|q\mathbf{x} -\mathbf{ p} \| \leqslant f(t).$
$\|q\mathbf{x} -\mathbf{ p} \| \leqslant f(t).$
8. Further applications
Most of the results described in this section are not proved in this paper; the proofs will appear elsewhere.
8.1 Irrationality measure functions and the Kan–Moshchevitin phenomenon
Another convenient way to describe various results in the theory of Diophantine approximation is through irrationality measure functions. Namely, given
![]() $A\in M_{m,n}(\mathbb{R})$
, one defines its irrationality measure function by
$A\in M_{m,n}(\mathbb{R})$
, one defines its irrationality measure function by
Then it is easy to see that A is f-uniformFootnote
4
if and only if
![]() $\psi_{A}(t) \leqslant f(t)$
for all large enough t. Similarly, for an arbitrary Diophantine system
$\psi_{A}(t) \leqslant f(t)$
for all large enough t. Similarly, for an arbitrary Diophantine system
![]() $\mathcal{X} = ( X, \mathcal{D}, \mathcal{H})$
one can introduce the irrationality measure function associated to
$\mathcal{X} = ( X, \mathcal{D}, \mathcal{H})$
one can introduce the irrationality measure function associated to
![]() $x\in X$
:
$x\in X$
:
Then
![]() $x\in \operatorname{UA}_{\mathcal{X}}(f)$
if and only if
$x\in \operatorname{UA}_{\mathcal{X}}(f)$
if and only if
![]() $\psi_x(t) \leqslant f(t)$
for all large enough t.
$\psi_x(t) \leqslant f(t)$
for all large enough t.
In 2009 the following result was proved by Kan and Moshchevitin [Reference Kan and MoshchevitinKM10]: in the standard Diophantine system corresponding to approximations to one real number (
![]() $m=n=1$
), for any two different real numbers x,y with
$m=n=1$
), for any two different real numbers x,y with
(a condition equivalent to
![]() $x,y\notin\mathbb{Q}$
), the difference
$x,y\notin\mathbb{Q}$
), the difference
![]() $\psi_x(t) -\psi_y(t)$
changes its sign infinitely often as
$\psi_x(t) -\psi_y(t)$
changes its sign infinitely often as
![]() $t \to \infty$
. This phenomenon is not present when
$t \to \infty$
. This phenomenon is not present when
![]() $\max(m,n) > 1$
. More generally, as long as the assumptions of our main theorem (Theorem 1.5) are satisfied, there exist pairs of points whose irrationality measure functions do not exhibit the pattern of infinitely many changes of sign. More precisely, suppose a Diophantine system
$\max(m,n) > 1$
. More generally, as long as the assumptions of our main theorem (Theorem 1.5) are satisfied, there exist pairs of points whose irrationality measure functions do not exhibit the pattern of infinitely many changes of sign. More precisely, suppose a Diophantine system
and a countable collection
![]() $\mathcal{L}$
of closed subsets of X satisfy the assumptions of Theorem 1.5 with
$\mathcal{L}$
of closed subsets of X satisfy the assumptions of Theorem 1.5 with
![]() $Y = X$
,
$Y = X$
,
![]() $\varphi_k\equiv \operatorname{Id}$
and
$\varphi_k\equiv \operatorname{Id}$
and
![]() $\mathcal{R} = \{{d_s}^{-1}(0) : s\in \mathcal{I}\}$
. Then for any
$\mathcal{R} = \{{d_s}^{-1}(0) : s\in \mathcal{I}\}$
. Then for any
![]() $x\in X$
such that
$x\in X$
such that
one can apply the theorem with
![]() $f = \psi_x$
and conclude that there exists a dense set of
$f = \psi_x$
and conclude that there exists a dense set of
![]() $y\in X$
such that
$y\in X$
such that
![]() $\psi_y(t) >0$
for all t and
$\psi_y(t) >0$
for all t and
![]() $\psi_y(t)< \psi_x(t)$
for all large enough t.
$\psi_y(t)< \psi_x(t)$
for all large enough t.
8.2 Inhomogeneous approximation and approximation with restrictions
It is natural to consider the problems of uniform approximation for systems of linear forms in the inhomogeneous set-up; that is, fix
![]() $\mathbf{b}\in\mathbb{R}^m$
and, instead of (1.2), look for non-trivial integer solutions of the system
$\mathbf{b}\in\mathbb{R}^m$
and, instead of (1.2), look for non-trivial integer solutions of the system
This calls for the consideration of the collection
and the proof of its total density for arbitrary
![]() $\mathbf{b}\in\mathbb{R}^n$
. And indeed it turns out to be possible to achieve this when
$\mathbf{b}\in\mathbb{R}^n$
. And indeed it turns out to be possible to achieve this when
![]() $n > 1$
, and thereby construct f-uniform systems of affine forms with an arbitrary fixed translation part. Moreover, in a forthcoming joint work with Hong and Neckrasov we take subsets P of
$n > 1$
, and thereby construct f-uniform systems of affine forms with an arbitrary fixed translation part. Moreover, in a forthcoming joint work with Hong and Neckrasov we take subsets P of
![]() $\mathbb{R}^m$
and Q of
$\mathbb{R}^m$
and Q of
![]() $\mathbb{Z}^n$
, and say that
$\mathbb{Z}^n$
, and say that
![]() $A\in M_{m,n}(\mathbb{R})$
is f-uniform with respect to (P,Q) if for all large enough
$A\in M_{m,n}(\mathbb{R})$
is f-uniform with respect to (P,Q) if for all large enough
![]() $t>0$
there exist
$t>0$
there exist
![]() $\textbf{q} \in Q$
and
$\textbf{q} \in Q$
and
![]() $\textbf{p} \in P$
satisfying (1.2). The classical theory of homogeneous approximation corresponds to
$\textbf{p} \in P$
satisfying (1.2). The classical theory of homogeneous approximation corresponds to
![]() $P = \mathbb{Z}^m$
and
$P = \mathbb{Z}^m$
and
![]() $Q = \mathbb{Z}^{{n}}\smallsetminus\{0\}$
. The following theorem can be proved (work in progress).
$Q = \mathbb{Z}^{{n}}\smallsetminus\{0\}$
. The following theorem can be proved (work in progress).
Theorem 8.1. The collection
![]() ${{\{L_{\textbf{p},\textbf{q}}}: \textbf{p}\in P,\,\textbf{q}\in Q\}}$
of subspaces of
${{\{L_{\textbf{p},\textbf{q}}}: \textbf{p}\in P,\,\textbf{q}\in Q\}}$
of subspaces of
![]() $M_{m,n}(\mathbb{R})$
is totally dense if:
$M_{m,n}(\mathbb{R})$
is totally dense if:
-
(a)
 $Q = \mathbb{Z}^n\smallsetminus\{0\}$
and P is a subgroup of
$Q = \mathbb{Z}^n\smallsetminus\{0\}$
and P is a subgroup of
 $\mathbb{Z}^m$
of rank
$\mathbb{Z}^m$
of rank
 $>m-n+1$
(restricted numerators);
$>m-n+1$
(restricted numerators); -
(b)
 $Q = Q_1\times\cdots\times Q_n\subset \mathbb{Z}\times\cdots\times\mathbb{Z}$
, where at least two of the sets
$Q = Q_1\times\cdots\times Q_n\subset \mathbb{Z}\times\cdots\times\mathbb{Z}$
, where at least two of the sets
 $Q_i$
are infinite (restricted denominators), and P is of bounded Hausdorff distance from
$Q_i$
are infinite (restricted denominators), and P is of bounded Hausdorff distance from
 $\mathbb{R}^m$
.
$\mathbb{R}^m$
.
Consequently (modulo Theorem 1.5) for any non-increasing
![]() $f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
the set of
$f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
the set of
![]() $m \times n$
matrices that are f-uniform with respect to (P,Q) and not contained in a given countable family of proper analytic submanifolds of
$m \times n$
matrices that are f-uniform with respect to (P,Q) and not contained in a given countable family of proper analytic submanifolds of
![]() $M_{m,n}(\mathbb{R})$
is uncountable and dense.
$M_{m,n}(\mathbb{R})$
is uncountable and dense.
Note that both (a) and (b) implicitly assume that
![]() $n > 1$
, and the set-up of (b) includes inhomogeneous approximation by letting
$n > 1$
, and the set-up of (b) includes inhomogeneous approximation by letting
![]() $P = \mathbb{Z}^m+\mathbf{b}$
for a fixed
$P = \mathbb{Z}^m+\mathbf{b}$
for a fixed
![]() $\mathbf{b}\in\mathbb{R}^m$
. When
$\mathbf{b}\in\mathbb{R}^m$
. When
![]() $n=1$
, it is clear that for any fixed
$n=1$
, it is clear that for any fixed
![]() $\mathbf{b}\in\mathbb{R}^m$
the collection (8.2) is not totally dense. On the other hand one can study a doubly metric version of the problem, that is, the set of pairs
$\mathbf{b}\in\mathbb{R}^m$
the collection (8.2) is not totally dense. On the other hand one can study a doubly metric version of the problem, that is, the set of pairs
![]() $(A,\mathbf{b}$
) such that (8.1) has a non-trivial integer solution for large enough t. It was recently documented by the second named author [Reference MoshchevitinMos24] that for any
$(A,\mathbf{b}$
) such that (8.1) has a non-trivial integer solution for large enough t. It was recently documented by the second named author [Reference MoshchevitinMos24] that for any
![]() $m\in\mathbb{N}$
and any non-increasing
$m\in\mathbb{N}$
and any non-increasing
![]() $f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
there exists a dense and uncountable set of pairs
$f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
there exists a dense and uncountable set of pairs
![]() $(\mathbf{x},\mathbf{y})\in\mathbb{R}^m\times \mathbb{R}^m \cong M_{m,2}$
such that the system of inequalities
$(\mathbf{x},\mathbf{y})\in\mathbb{R}^m\times \mathbb{R}^m \cong M_{m,2}$
such that the system of inequalities
has a nonzero integer solution
![]() $(\textbf{p},q)$
for all large enough t. In fact, this statement follows from a old result by Khintchine [Reference KhintchineKhi47] which is not very well known. See also [Reference Moshchevitin and NeckrasovMN25, 3.3] for a discussion.
$(\textbf{p},q)$
for all large enough t. In fact, this statement follows from a old result by Khintchine [Reference KhintchineKhi47] which is not very well known. See also [Reference Moshchevitin and NeckrasovMN25, 3.3] for a discussion.
8.3 Rational approximations to linear subspaces
In this subsection we fix
![]() $d\in\mathbb{N}_{\geqslant2}$
and
$d\in\mathbb{N}_{\geqslant2}$
and
![]() $a = 1,\dots, d-1$
, and consider a certain Diophantine system on
$a = 1,\dots, d-1$
, and consider a certain Diophantine system on
![]() $X = \operatorname{Gr}_{d,a}$
, the Grassmannian of a-dimensional subspaces of
$X = \operatorname{Gr}_{d,a}$
, the Grassmannian of a-dimensional subspaces of
![]() $\mathbb{R}^d$
. Following the set-up of [Reference SchmidtSch67], one can study the problems of approximation of an a-dimensional subspace A of
$\mathbb{R}^d$
. Following the set-up of [Reference SchmidtSch67], one can study the problems of approximation of an a-dimensional subspace A of
![]() $\mathbb{R}^d$
by b-dimensional rational subspaces B of
$\mathbb{R}^d$
by b-dimensional rational subspaces B of
![]() $\mathbb{R}^d$
, where
$\mathbb{R}^d$
, where
![]() $1\leqslant b < d$
, in terms of the so-called first angle between the subspaces. The latter (or rather, formally speaking, the sine of the angle) is defined as follows:
$1\leqslant b < d$
, in terms of the so-called first angle between the subspaces. The latter (or rather, formally speaking, the sine of the angle) is defined as follows:
where
![]() $\|\cdot\|$
is the Euclidean norm on
$\|\cdot\|$
is the Euclidean norm on
![]() $\mathbb{R}^d$
and on
$\mathbb{R}^d$
and on
![]() $\bigwedge^2(\mathbb{R}^d)$
.
$\bigwedge^2(\mathbb{R}^d)$
.
Note that
![]() $\measuredangle_1 (A,B) = 0$
if and only if
$\measuredangle_1 (A,B) = 0$
if and only if
![]() $\dim(A\cap B) >0$
. Using the terminology introduced in [Reference NeckrasovNec22], let us say that
$\dim(A\cap B) >0$
. Using the terminology introduced in [Reference NeckrasovNec22], let us say that
![]() $A\in \operatorname{Gr}_{d,a}$
is completely irrational if for any
$A\in \operatorname{Gr}_{d,a}$
is completely irrational if for any
![]() $(d-a)$
-dimensional rational subspace R we have
$(d-a)$
-dimensional rational subspace R we have
![]() $A\cap R = \{{0}\}$
. We also define the height H(B) of a rational subspace
$A\cap R = \{{0}\}$
. We also define the height H(B) of a rational subspace
![]() $B\subset \mathbb{R}^d$
of dimension b in the natural way as the covolume of the b-dimensional lattice
$B\subset \mathbb{R}^d$
of dimension b in the natural way as the covolume of the b-dimensional lattice
![]() $ B\cap \mathbb{Z}^d$
. Using the methods of this paper, namely Theorem 1.5, it is possible to prove the following theorem.
$ B\cap \mathbb{Z}^d$
. Using the methods of this paper, namely Theorem 1.5, it is possible to prove the following theorem.
Theorem 8.2.
Let
![]() $1\leqslant a,b < d$
with
$1\leqslant a,b < d$
with
![]() $\max(a,b) > 1$
. Then for any non-increasing
$\max(a,b) > 1$
. Then for any non-increasing
![]() $f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
the set of completely irrational
$f: \mathbb{R}_{>0} \to \mathbb{R}_{>0}$
the set of completely irrational
![]() $A\in \operatorname{Gr}_{d,a}$
such that the system of inequalities
$A\in \operatorname{Gr}_{d,a}$
such that the system of inequalities
has a solution in b-dimensional rational subspaces B for all large enough t is uncountable and dense.
The case
![]() $d=4$
and
$d=4$
and
![]() $a=b=2$
is a recent result of Chebotarenko [Reference ChebotarenkoChe24]. The above theorem, as well as several generalizations, will be proved in a forthcoming work.
$a=b=2$
is a recent result of Chebotarenko [Reference ChebotarenkoChe24]. The above theorem, as well as several generalizations, will be proved in a forthcoming work.
Acknowledgements
The authors thank Yitwah Cheung, Vasiliy Neckrasov, Nicolas de Saxcé and Damien Roy for helpful discussions. Thanks are also due to the anonymous referee for a careful reading of the paper and many insightful comments.
Conflicts of interest
None.
Financial support
The authors are grateful for funding by the National Science Foundation under grant DMS-2155111, the Austrian Science Fund (FWF), Forschungsprojekt PAT1961524, the Israel Science Foundation under grants ISF 2019/19 and ISF-NSFC 3739/21, and the Zuckerman STEM Leadership Program.
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.