Hostname: page-component-89b8bd64d-46n74 Total loading time: 0 Render date: 2026-05-08T00:48:04.158Z Has data issue: false hasContentIssue false
  • English
  • Français

The smooth locus in infinite-level Rapoport–Zink spaces

Part of: Algebraic groups Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  03 November 2020

Alexander B. Ivanov  and
Jared Weinstein
Alexander B. Ivanov
Affiliation:
Mathematisches Institut, Universität Bonn, Endenicher Allee 60, 53115 Bonn, Germany ivanov@math.uni-bonn.de
Jared Weinstein
Affiliation:
Department of Mathematics and Statistics, Boston University, Boston, MA 02215, USA jsweinst@math.bu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Rapoport–Zink spaces are deformation spaces for 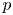$p$-divisible groups with additional structure. At infinite level, they become preperfectoid spaces. Let 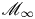${{\mathscr M}}_{\infty }$ be an infinite-level Rapoport–Zink space of EL type, and let ${{\mathscr M}}_{\infty }^{\circ }$ be one connected component of its geometric fiber. We show that 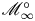${{\mathscr M}}_{\infty }^{\circ }$ contains a dense open subset which is cohomologically smooth in the sense of Scholze. This is the locus of 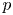$p$-divisible groups which do not have any extra endomorphisms. As a corollary, we find that the cohomologically smooth locus in the infinite-level modular curve 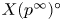$X(p^{\infty })^{\circ }$ is exactly the locus of elliptic curves 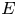$E$ with supersingular reduction, such that the formal group of 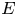$E$ has no extra endomorphisms.

Keywords

p-divisible groupsRapoport–Zink spacesperfectoid spacesvector bundles on the Fargues–Fontaine curvecohomological smoothness

MSC classification

Primary: 14G22: Rigid analytic geometry 14L05: Formal groups, $p$-divisible groups

Information

Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 9 , September 2020 , pp. 1846 - 1872
Check for updates
Copyright
Copyright © The Author(s) 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 21 (Springer, Berlin, 1990).Google Scholar
Chen, M., Composantes connexes géométriques de la tour des espaces de modules de groupes $p$-divisibles, Ann. Sci. Éc. Norm. Supér. (4) 47 (2014), 723–764.CrossRefGoogle Scholar
Fargues, L. and Fontaine, J.-M., Courbes et fibrés vectoriels en theorie de Hodge p-adique, Astérisque 406 (2018).10.24033/ast.1056CrossRefGoogle Scholar
Fargues, L. and Scholze, P., Geometrization of the local Langlands correspondence, in preparation.Google Scholar
Kottwitz, R. E., Isocrystals with additional structure, Compos. Math. 56 (1985), 201–220.Google Scholar
Le Bras, A.-C., Espaces de Banach–Colmez et faisceaux cohérents sur la courbe de Fargues–Fontaine, Duke Math. J. 167 (2018), 3455–3532.Google Scholar
Messing, W., The crystals associated to Barsotti-Tate groups: with applications to abelian schemes, Lecture Notes in Mathematics, vol. 264 (Springer, New York, NY, 1972).CrossRefGoogle Scholar
Rapoport, M. and Zink, T., Period spaces for p-divisible groups, Annals of Mathematics Studies, vol. 141 (Princeton University Press, Princeton, NJ, 1996).Google Scholar
Scholze, P., On torsion in the cohomology of locally symmetric varieties, Ann. Math. (2) 182 (2015), 945–1066.CrossRefGoogle Scholar
Scholze, P., The étale cohomology of diamonds, Preprint (2017), arXiv:1709.07343.Google Scholar
Scholze, P. and Weinstein, J., Moduli of p-divisible groups, Camb. J. Math. 1 (2013), 145–237.10.4310/CJM.2013.v1.n2.a1CrossRefGoogle Scholar
The Stacks Project Authors, Stacks project (2014), http://stacks.math.columbia.edu.Google Scholar
Weinstein, J., Semistable models for modular curves of arbitrary level, Invent. Math. 205 (2016), 459–526.CrossRefGoogle Scholar