Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yoshioka, Kōta
2009.
Fourier–Mukai transform on abelian surfaces.
Mathematische Annalen,
Vol. 345,
Issue. 3,
p.
493.
KIMURA, Masanori
and
YOSHIOKA, Kōta
2011.
Birational Maps of Moduli Spaces of Vector Bundles on $K3$ Surfaces.
Tokyo Journal of Mathematics,
Vol. 34,
Issue. 2,
Bayer, Arend
and
Macrì, Emanuele
2011.
The space of stability conditions on the local projective plane.
Duke Mathematical Journal,
Vol. 160,
Issue. 2,
Yoshioka, Kōta
2013.
Perverse coherent sheaves and Fourier–Mukai transforms on surfaces, I.
Kyoto Journal of Mathematics,
Vol. 53,
Issue. 2,
Kawatani, Kotaro
2013.
Stability of Gieseker stable sheaves on K3 surfaces in the sense of Bridgeland and some applications.
Kyoto Journal of Mathematics,
Vol. 53,
Issue. 3,
Maciocia, Antony
and
Meachan, Ciaran
2013.
Rank 1 Bridgeland Stable Moduli Spaces on A Principally Polarized Abelian Surface.
International Mathematics Research Notices,
Vol. 2013,
Issue. 9,
p.
2054.
Yanagida, Shintarou
and
Yoshioka, Kōta
2014.
Bridgeland’s stabilities on abelian surfaces.
Mathematische Zeitschrift,
Vol. 276,
Issue. 1-2,
p.
571.
Minamide, Hiroki
Yanagida, Shintarou
and
Yoshioka, Kōta
2014.
Some Moduli Spaces of Bridgeland’s Stability Conditions.
International Mathematics Research Notices,
Vol. 2014,
Issue. 19,
p.
5264.
Yoshioka, Kōta
2015.
Perverse coherent sheaves and Fourier–Mukai transforms on surfaces, II.
Kyoto Journal of Mathematics,
Vol. 55,
Issue. 2,
Maciocia, Antony
and
Piyaratne, Dulip
2016.
Fourier–Mukai transforms and Bridgeland stability conditions on abelian threefolds II.
International Journal of Mathematics,
Vol. 27,
Issue. 01,
p.
1650007.
Sawon, Justin
2016.
Moduli spaces of sheaves on K3 surfaces.
Journal of Geometry and Physics,
Vol. 109,
Issue. ,
p.
68.
Yoshioka, Kōta
2017.
Fourier–Mukai duality for K3 surfaces via Bridgeland stability condition.
Journal of Geometry and Physics,
Vol. 122,
Issue. ,
p.
103.
Huybrechts, Daniel
2017.
The K3 category of a cubic fourfold.
Compositio Mathematica,
Vol. 153,
Issue. 3,
p.
586.
Yoshioka, Kōta
2017.
A note on stable sheaves on Enriques surfaces.
Tohoku Mathematical Journal,
Vol. 69,
Issue. 3,
Minamide, Hiroki
Yanagida, Shintarou
and
Yoshioka, Kōta
2018.
The wall-crossing behavior for Bridgeland’s stability conditions on abelian and K3 surfaces.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2018,
Issue. 735,
p.
1.
Yoshioka, Kōta
2018.
Moduli spaces of stable sheaves on Enriques surfaces.
Kyoto Journal of Mathematics,
Vol. 58,
Issue. 4,
Arbarello, E.
and
Saccà, G.
2018.
Singularities of moduli spaces of sheaves on K3 surfaces and Nakajima quiver varieties.
Advances in Mathematics,
Vol. 329,
Issue. ,
p.
649.
Budur, Nero
and
Zhang, Ziyu
2019.
Formality conjecture for K3 surfaces.
Compositio Mathematica,
Vol. 155,
Issue. 5,
p.
902.
Piyaratne, Dulip
2019.
Stability Conditions Under the Fourier–Mukai Transforms on Abelian 3-folds.
The Quarterly Journal of Mathematics,
Vol. 70,
Issue. 1,
p.
225.
Nuer, Howard
and
Yoshioka, Kōta
2020.
MMP via wall-crossing for moduli spaces of stable sheaves on an Enriques surface.
Advances in Mathematics,
Vol. 372,
Issue. ,
p.
107283.

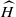 on
on 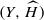 . We show that the stability with respect to these polarizations is preserved under ℱ
. We show that the stability with respect to these polarizations is preserved under ℱ