Article contents
Stability in the high-dimensional cohomology of congruence subgroups
Published online by Cambridge University Press: 24 March 2020
Abstract
We prove a representation stability result for the codimension-one cohomology of the level-three congruence subgroup of 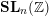 $\mathbf{SL}_{n}(\mathbb{Z})$. This is a special case of a question of Church, Farb, and Putman which we make more precise. Our methods involve proving finiteness properties of the Steinberg module for the group
$\mathbf{SL}_{n}(\mathbb{Z})$. This is a special case of a question of Church, Farb, and Putman which we make more precise. Our methods involve proving finiteness properties of the Steinberg module for the group 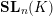 $\mathbf{SL}_{n}(K)$ for
$\mathbf{SL}_{n}(K)$ for 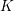 $K$ a field. This also lets us give a new proof of Ash, Putman, and Sam’s homological vanishing theorem for the Steinberg module. We also prove an integral refinement of Church and Putman’s homological vanishing theorem for the Steinberg module for the group
$K$ a field. This also lets us give a new proof of Ash, Putman, and Sam’s homological vanishing theorem for the Steinberg module. We also prove an integral refinement of Church and Putman’s homological vanishing theorem for the Steinberg module for the group 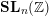 $\mathbf{SL}_{n}(\mathbb{Z})$.
$\mathbf{SL}_{n}(\mathbb{Z})$.
Information
- Type
- Research Article
- Information
- Copyright
- © The Authors 2020
Footnotes
Jeremy Miller was supported in part by NSF grant DMS-1709726.
References
- 8
- Cited by

