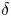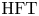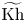1. Introduction
Fox famously asked
What is an alternating knot?
He was interested in knowing if this property could be characterized without reference to knot diagrams; see Lickorish [Reference LickorishLic97, Chapter 4]. A satisfying answer to Fox's question was provided by Greene [Reference GreeneGre17] and Howie [Reference HowieHow17]: both works prove that a non-split link is alternating if and only if it admits a pair of special spanning surfaces.
Bar-Natan conjectured [Reference Bar-NatanBN02] and Lee proved [Reference LeeLee05] that alternating links have thin Khovanov homology. Subsequently, Ozsváth and Szabó proved that alternating links have thin knot Floer homology [Reference Ozsváth and SzabóOS03a, Reference Ozsváth and SzabóOS08]. That is, the relevant bigraded homology theory in each case is supported along a single diagonal (taking the reduced version in the case of Khovanov's invariant). These diagonals give rise to the integer-valued ![]() $\delta$-grading in each theory, so that thinness is defined, algebraically, as follows.
$\delta$-grading in each theory, so that thinness is defined, algebraically, as follows.
Definition 1.1 A ![]() $\delta$-graded vector space is called thin if it is supported in at most one
$\delta$-graded vector space is called thin if it is supported in at most one ![]() $\delta$-grading.
$\delta$-grading.
A link is called thin if its associated invariant is thin. Bar-Natan's calculations showed that non-alternating thin links exist in Khovanov homology, suggesting a broader class of links that appears harder to pin down. Restricting coefficients to the rational numbers for the moment, Dowlin's spectral sequence from Khovanov homology to knot Floer homology [Reference DowlinDow18] implies that if a link is thin as measured by Khovanov homology then it must be thin as measured by knot Floer homology. In fact, computations suggest that these notions of thinness coincide. Thus, the question
What is a thin link?
is a natural one. In particular, is there a characterization of thinness that does not depend on the bigraded link homology theory used? For example, quasi-alternating links were proved to be thin by Manolescu and Ozsváth [Reference Manolescu and OzsváthMO08]. Interestingly, thin links that are not quasi-alternating exist [Reference GreeneGre10] and indeed arise in infinite families [Reference Greene and WatsonGW13]. A larger class has been proposed, two-fold quasi-alternating [Reference Scaduto and StoffregenSS18], and one might ask whether this exactly captures the property of being thin.
Beyond the homology theory in question, thinness may also depend on the coefficient system. Indeed, Shumakovitch found a knot whose Khovanov homology is thin when computed over ![]() $\mathbb {Q}$, but not over the two-element field
$\mathbb {Q}$, but not over the two-element field ![]() $\mathbb {F}$ (see [Reference ShumakovitchShu21]); see Example 7.1 for further discussion. The authors are unaware of any such example for knot Floer homology.
$\mathbb {F}$ (see [Reference ShumakovitchShu21]); see Example 7.1 for further discussion. The authors are unaware of any such example for knot Floer homology.
A change of perspective
The question ‘What is a thin link?’ may be placed in a broader context: Given any homology theory ![]() $\operatorname {\mathbf {H}_\ast }$ (of CW-complexes, manifolds, links, etc.), a basic observation is that its dimension is bounded below by the absolute value of its Euler characteristic
$\operatorname {\mathbf {H}_\ast }$ (of CW-complexes, manifolds, links, etc.), a basic observation is that its dimension is bounded below by the absolute value of its Euler characteristic ![]() $\chi$. Thus, the following is a natural problem.
$\chi$. Thus, the following is a natural problem.
Problem 1.2 Characterize the objects ![]() $Y$ for which
$Y$ for which ![]() $\dim \operatorname {\mathbf {H}_\ast }(Y)=|\chi \operatorname {\mathbf {H}_\ast }(Y)|$.
$\dim \operatorname {\mathbf {H}_\ast }(Y)=|\chi \operatorname {\mathbf {H}_\ast }(Y)|$.
Equivalently, the problem is to classify all objects whose homology is supported in gradings of the same parity. Even for singular homology of manifolds, this appears to be a hard question, although some basic facts can be easily established: for oriented two-dimensional manifolds, for example, the identity ![]() $\dim \operatorname {\mathbf {H}_\ast }(Y)=|\chi \operatorname {\mathbf {H}_\ast }(Y)|$ characterizes the two-sphere. For unoriented two-dimensional manifolds, the situation already becomes more subtle, because the answer depends on the field of coefficients. For
$\dim \operatorname {\mathbf {H}_\ast }(Y)=|\chi \operatorname {\mathbf {H}_\ast }(Y)|$ characterizes the two-sphere. For unoriented two-dimensional manifolds, the situation already becomes more subtle, because the answer depends on the field of coefficients. For ![]() $n$ odd, the Euler characteristic of any
$n$ odd, the Euler characteristic of any ![]() $n$-dimensional closed manifold vanishes, so there are no solutions to this identity. A naïve guess for even integers
$n$-dimensional closed manifold vanishes, so there are no solutions to this identity. A naïve guess for even integers ![]() $n\geq 4$ would be that solutions should admit a handle decomposition with no
$n\geq 4$ would be that solutions should admit a handle decomposition with no ![]() $i$-handles for odd
$i$-handles for odd ![]() $i$. But such a characterization seems to be difficult to establish even for closed, simply connected four-manifolds; see [Reference KirbyKir95, Problem 4.18].
$i$. But such a characterization seems to be difficult to establish even for closed, simply connected four-manifolds; see [Reference KirbyKir95, Problem 4.18].
In the context of Ozsváth and Szabó's Heegaard Floer homology ![]() $\operatorname {\widehat {HF}}$ for closed oriented three-manifolds, solutions to
$\operatorname {\widehat {HF}}$ for closed oriented three-manifolds, solutions to ![]() $\dim \operatorname {\widehat {HF}}(Y)=|\chi \operatorname {\widehat {HF}}(Y)|$ are known under the name L-spaces; see § 7.5 for a detailed discussion of this definition. In this context, Problem 1.2 relates to the question
$\dim \operatorname {\widehat {HF}}(Y)=|\chi \operatorname {\widehat {HF}}(Y)|$ are known under the name L-spaces; see § 7.5 for a detailed discussion of this definition. In this context, Problem 1.2 relates to the question
What is an L-space?
(see [Reference Ozsváth and SzabóOS05a, Question 11]), which continues to drive research. Ozsváth and Szabó proved that L-spaces cannot carry taut foliations [Reference Ozsváth and SzabóOS04a] (see also [Reference BowdenBow16, Reference Kazez and RobertsKR17]). At present, the conditions ![]() $Y$ not being an L-space,
$Y$ not being an L-space, ![]() $\pi _1(Y)$ being left-orderable, and
$\pi _1(Y)$ being left-orderable, and ![]() $Y$ admitting a taut foliation are known to be equivalent for all graph manifolds [Reference Boyer and ClayBC17, Reference RasmussenRas17, Reference Hanselman, Rasmussen, Rasmussen and WatsonHRRW20]. The equivalence of these three conditions is conjectured in general; see [Reference Boyer, Gordon and WatsonBGW13] or [Reference DunfieldDun20] for further discussion.
$Y$ admitting a taut foliation are known to be equivalent for all graph manifolds [Reference Boyer and ClayBC17, Reference RasmussenRas17, Reference Hanselman, Rasmussen, Rasmussen and WatsonHRRW20]. The equivalence of these three conditions is conjectured in general; see [Reference Boyer, Gordon and WatsonBGW13] or [Reference DunfieldDun20] for further discussion.
Turning now to link homology theories: the reduced Khovanov homology ![]() $\widetilde {\operatorname {Kh}}(L;{\mathbf {k}})$ of an
$\widetilde {\operatorname {Kh}}(L;{\mathbf {k}})$ of an ![]() $\ell$-component link
$\ell$-component link ![]() $L$ in
$L$ in ![]() $S^3$ categorifies the Jones polynomial
$S^3$ categorifies the Jones polynomial ![]() $V_L(t)$, in the sense that
$V_L(t)$, in the sense that
where ![]() $h$ denotes the homological grading,
$h$ denotes the homological grading, ![]() $q$ the quantum grading, and
$q$ the quantum grading, and ![]() ${\mathbf {k}}$ is some field. By setting
${\mathbf {k}}$ is some field. By setting ![]() $t=1$, we see that the ungraded Euler characteristic with respect to the homological grading is equal to
$t=1$, we see that the ungraded Euler characteristic with respect to the homological grading is equal to ![]() $V_L(1)=2^{\ell -1}$. Problem 1.2 in this setting was recently solved by Xie and Zhang [Reference Xie and ZhangXZ18], who showed that the identity
$V_L(1)=2^{\ell -1}$. Problem 1.2 in this setting was recently solved by Xie and Zhang [Reference Xie and ZhangXZ18], who showed that the identity ![]() $\dim \widetilde {\operatorname {Kh}}(L;{\mathbf {k}})=|\chi _h\widetilde {\operatorname {Kh}}(L;{\mathbf {k}})|=2^{\ell -1}$ characterizes so-called forests of unknots (at least if
$\dim \widetilde {\operatorname {Kh}}(L;{\mathbf {k}})=|\chi _h\widetilde {\operatorname {Kh}}(L;{\mathbf {k}})|=2^{\ell -1}$ characterizes so-called forests of unknots (at least if ![]() ${\mathbf {k}}=\mathbb {F}$). Similarly, the knot Floer homology
${\mathbf {k}}=\mathbb {F}$). Similarly, the knot Floer homology ![]() $\operatorname {\widehat {HFK}}(L;{\mathbf {k}})$ categorifies the Alexander polynomial
$\operatorname {\widehat {HFK}}(L;{\mathbf {k}})$ categorifies the Alexander polynomial ![]() $\Delta _L(t)$:
$\Delta _L(t)$:
where ![]() $h$ denotes the homological grading (often called the Maslov grading) and
$h$ denotes the homological grading (often called the Maslov grading) and ![]() $A$ denotes the Alexander grading (or, more precisely, twice the Alexander grading from [Reference Ozsváth and SzabóOS04b]). The ungraded Euler characteristic with respect to the homological grading is equal to
$A$ denotes the Alexander grading (or, more precisely, twice the Alexander grading from [Reference Ozsváth and SzabóOS04b]). The ungraded Euler characteristic with respect to the homological grading is equal to ![]() $0$ if
$0$ if ![]() $\ell >1$ and
$\ell >1$ and ![]() $\Delta _L(1)=1$ if
$\Delta _L(1)=1$ if ![]() $\ell =1$. Thus, in the first case, there are no solutions to the identity
$\ell =1$. Thus, in the first case, there are no solutions to the identity ![]() $\dim \operatorname {\widehat {HFK}}(L;{\mathbf {k}})=|\chi _h\operatorname {\widehat {HFK}}(L;{\mathbf {k}})|$; in the second case, Problem 1.2 reduces to the question about unknot detection for
$\dim \operatorname {\widehat {HFK}}(L;{\mathbf {k}})=|\chi _h\operatorname {\widehat {HFK}}(L;{\mathbf {k}})|$; in the second case, Problem 1.2 reduces to the question about unknot detection for ![]() $\operatorname {\widehat {HFK}}$, which was settled by Ozsváth and Szabó [Reference Ozsváth and SzabóOS04a].
$\operatorname {\widehat {HFK}}$, which was settled by Ozsváth and Szabó [Reference Ozsváth and SzabóOS04a].
Since both ![]() $\widetilde {\operatorname {Kh}}$ and
$\widetilde {\operatorname {Kh}}$ and ![]() $\operatorname {\widehat {HFK}}$ are bigraded homology theories, one is not restricted to taking Euler characteristics with respect to the homological grading. Another choice is the
$\operatorname {\widehat {HFK}}$ are bigraded homology theories, one is not restricted to taking Euler characteristics with respect to the homological grading. Another choice is the ![]() $\delta$-grading, which is defined by
$\delta$-grading, which is defined by ![]() $\delta =\frac {1}{2}q-h$ and
$\delta =\frac {1}{2}q-h$ and ![]() $\delta =\frac {1}{2}A-h$, respectively. This corresponds to setting
$\delta =\frac {1}{2}A-h$, respectively. This corresponds to setting ![]() $t=-1$ in the polynomial invariants:
$t=-1$ in the polynomial invariants:
 \begin{align*} \chi_{\delta}\widetilde{\operatorname{Kh}}(L;{\mathbf{k}}) &:= \sum (-1)^{h+\frac{1}{2}q} \dim \widetilde{\operatorname{Kh}}{}^{h,q}(L;{\mathbf{k}}) = V_L(-1)\\ \chi_{\delta}\operatorname{\widehat{HFK}}(L;{\mathbf{k}}) &:= \sum (-1)^{h+\frac{1}{2}A} \dim \operatorname{\widehat{HFK}}{}^{h,A}(L;{\mathbf{k}}) =\pm 2^{\ell-1}\cdot\Delta_L(-1). \end{align*}
\begin{align*} \chi_{\delta}\widetilde{\operatorname{Kh}}(L;{\mathbf{k}}) &:= \sum (-1)^{h+\frac{1}{2}q} \dim \widetilde{\operatorname{Kh}}{}^{h,q}(L;{\mathbf{k}}) = V_L(-1)\\ \chi_{\delta}\operatorname{\widehat{HFK}}(L;{\mathbf{k}}) &:= \sum (-1)^{h+\frac{1}{2}A} \dim \operatorname{\widehat{HFK}}{}^{h,A}(L;{\mathbf{k}}) =\pm 2^{\ell-1}\cdot\Delta_L(-1). \end{align*}
This choice seems to be particularly natural, since
where ![]() $\det (L)$ is the determinant of
$\det (L)$ is the determinant of ![]() $L$, a classical link invariant. It leads us to consider the following.
$L$, a classical link invariant. It leads us to consider the following.
Definition 1.3 Given a link homology theory ![]() $\operatorname {\mathbf {H}_\ast }$, an A-link is a link
$\operatorname {\mathbf {H}_\ast }$, an A-link is a link ![]() $L$ satisfying
$L$ satisfying
In the following, ![]() $\operatorname {\mathbf {H}_\ast }$ will be either
$\operatorname {\mathbf {H}_\ast }$ will be either ![]() $\widetilde {\operatorname {Kh}}$ or
$\widetilde {\operatorname {Kh}}$ or ![]() $\operatorname {\widehat {HFK}}$ with coefficients in some field
$\operatorname {\widehat {HFK}}$ with coefficients in some field ![]() ${\mathbf {k}}$. Again, there is a dependence on the homology theory
${\mathbf {k}}$. Again, there is a dependence on the homology theory ![]() $\mathbf {H}_*$ as well as on
$\mathbf {H}_*$ as well as on ![]() ${\mathbf {k}}$, and we will be adding the relevant modifiers where needed. Problem 1.2 relates to the question
${\mathbf {k}}$, and we will be adding the relevant modifiers where needed. Problem 1.2 relates to the question
What is an A-link?
By this question we are interested in knowing if this property can be described (geometrically or topologically) without reference to a link homology theory. Clearly, every thin link is an A-link. For ![]() $\operatorname {\mathbf {H}_\ast }=\operatorname {\widehat {HFK}}$, the converse is false, as the family of twisted Whitehead doubles of the trefoil knot that Hedden and Ording consider in [Reference Hedden and OrdingHO08] illustrates; see Example 7.15. For
$\operatorname {\mathbf {H}_\ast }=\operatorname {\widehat {HFK}}$, the converse is false, as the family of twisted Whitehead doubles of the trefoil knot that Hedden and Ording consider in [Reference Hedden and OrdingHO08] illustrates; see Example 7.15. For ![]() $\operatorname {\mathbf {H}_\ast }=\widetilde {\operatorname {Kh}}$, we expect that all A-links are thin. This is closely related to the question of full support.
$\operatorname {\mathbf {H}_\ast }=\widetilde {\operatorname {Kh}}$, we expect that all A-links are thin. This is closely related to the question of full support.
Definition 1.4 We say that a link homology theory ![]() $\operatorname {\mathbf {H}_\ast }$ has full support if for all links
$\operatorname {\mathbf {H}_\ast }$ has full support if for all links ![]() $L$ and all
$L$ and all ![]() $\delta$-gradings
$\delta$-gradings ![]() $i< j< k$,
$i< j< k$,
Proposition 1.5 Given a link homology theory ![]() $\operatorname {\mathbf {H}_\ast }$ with full support, a link is thin if and only if it is an A-link.
$\operatorname {\mathbf {H}_\ast }$ with full support, a link is thin if and only if it is an A-link.
Proof. A link ![]() $L$ is an A-link if and only if
$L$ is an A-link if and only if ![]() $\mathbf {H}_*(L)$ is supported in gradings of the same parity. Assuming
$\mathbf {H}_*(L)$ is supported in gradings of the same parity. Assuming ![]() $\operatorname {\mathbf {H}_\ast }$ has full support, the latter is equivalent to
$\operatorname {\mathbf {H}_\ast }$ has full support, the latter is equivalent to ![]() $\mathbf {H}_*(L)$ being supported in a single grading, i.e.
$\mathbf {H}_*(L)$ being supported in a single grading, i.e. ![]() $L$ being thin.
$L$ being thin.
To the best of the authors’ knowledge, there is no known example of a link violating full support for Khovanov homology: indeed, that this invariant has full support appears to be a folklore conjecture.
Our shift in perspective from thin links to A-links is primarily motivated by the observation that the latter are better behaved with respect to tangle decompositions along Conway spheres, which is the focus of this article. Another reason is the interplay between L-spaces and A-links in the context of two-fold branched covers: there is a spectral sequence due to Ozsváth and Szabó relating the reduced Khovanov homology of a link and the Heegaard Floer homology of the mirror of the two-fold branched cover of the link [Reference Ozsváth and SzabóOS05b]. In particular, given an A-link, the associated two-fold branched cover is an L-space. However, the converse is not true: the Poincaré homology sphere is an L-space that may be obtained as the two-fold branched cover of the torus knot ![]() $10_{124}$, which is not an A-knot. Nonetheless, there is a sense in which A-link branch sets might be characterized by sufficiently large L-space surgeries on strongly invertible knots; see the discussion in § 7, as well as [Reference WatsonWat17, Conjecture 30] and [Reference WatsonWat11] for related examples.
$10_{124}$, which is not an A-knot. Nonetheless, there is a sense in which A-link branch sets might be characterized by sufficiently large L-space surgeries on strongly invertible knots; see the discussion in § 7, as well as [Reference WatsonWat17, Conjecture 30] and [Reference WatsonWat11] for related examples.
Thin links and Conway spheres
For simplicity, we now restrict to coefficients in the field of two elements ![]() $\mathbb {F}$. We focus on characterizing thin links and A-links from the perspective of Conway spheres. This is motivated, in part, by results characterizing L-spaces in the presence of an essential torus. Given a three-manifold with torus boundary
$\mathbb {F}$. We focus on characterizing thin links and A-links from the perspective of Conway spheres. This is motivated, in part, by results characterizing L-spaces in the presence of an essential torus. Given a three-manifold with torus boundary ![]() $M$ and a parametrization of
$M$ and a parametrization of ![]() $\partial M$ by a meridian
$\partial M$ by a meridian ![]() $\mu$ and a longitude
$\mu$ and a longitude ![]() $\lambda$, the space of L-space fillings of
$\lambda$, the space of L-space fillings of ![]() $M$ is defined by
$M$ is defined by
where ![]() $M({p}/{q})$ is the closed three-manifold obtained by Dehn filling along the slope
$M({p}/{q})$ is the closed three-manifold obtained by Dehn filling along the slope ![]() $p\mu +q\lambda \in H_1(\partial M)$. Rasmussen and Rasmussen showed [Reference Rasmussen and RasmussenRR17, Proposition 1.3 and Theorem 1.6] the following.
$p\mu +q\lambda \in H_1(\partial M)$. Rasmussen and Rasmussen showed [Reference Rasmussen and RasmussenRR17, Proposition 1.3 and Theorem 1.6] the following.
Theorem 1.6 For any three-manifold with torus boundary ![]() $M$,
$M$, ![]() $\mathcal {L}(M)$ is either empty, a single point, a closed interval or
$\mathcal {L}(M)$ is either empty, a single point, a closed interval or ![]() $\operatorname {\mathbb {Q}P}^1$ minus a single point.
$\operatorname {\mathbb {Q}P}^1$ minus a single point.
Denote the interior of ![]() $\mathcal {L}(M)$ by
$\mathcal {L}(M)$ by ![]() $\mathring {\mathcal {L}}(M)$. Hanselman, Rasmussen, and the second author established the following result [Reference Hanselman, Rasmussen and WatsonHRW24, Theorem 13].
$\mathring {\mathcal {L}}(M)$. Hanselman, Rasmussen, and the second author established the following result [Reference Hanselman, Rasmussen and WatsonHRW24, Theorem 13].
Theorem 1.7 (L-space gluing theorem)
Let ![]() $Y = M_0 \cup _h M_1$ be a three-manifold where the
$Y = M_0 \cup _h M_1$ be a three-manifold where the ![]() $M_i$ are boundary incompressible manifolds and
$M_i$ are boundary incompressible manifolds and ![]() $h\colon \thinspace \partial M_1 \rightarrow \partial M_0$ is an orientation-reversing homeomorphism between the torus boundaries. Then
$h\colon \thinspace \partial M_1 \rightarrow \partial M_0$ is an orientation-reversing homeomorphism between the torus boundaries. Then ![]() $Y$ is an L-space if and only if
$Y$ is an L-space if and only if
A similar result holds without the assumption that ![]() $M_i$ be boundary incompressible; see Remark 7.16.
$M_i$ be boundary incompressible; see Remark 7.16.
A Conway tangle is a proper embedding of two intervals and a finite (possibly empty) set of circles into a closed 3-dimensional ball. We consider Conway tangles up to isotopy fixing the boundary sphere pointwise. Given a Conway tangle ![]() $T$ and a
$T$ and a ![]() $\delta$-graded link homology theory, we make analogous definitions:
$\delta$-graded link homology theory, we make analogous definitions:
 \begin{align*} \mathrm{A}(T) &:= \{ {p}/{q}\in\operatorname{\mathbb{Q}P}^1 \mid T({p}/{q}) \text{ is an A-link}\},\\ \Theta(T) &:= \{ {p}/{q}\in\operatorname{\mathbb{Q}P}^1 \mid T({p}/{q}) \text{ is thin} \}. \end{align*}
\begin{align*} \mathrm{A}(T) &:= \{ {p}/{q}\in\operatorname{\mathbb{Q}P}^1 \mid T({p}/{q}) \text{ is an A-link}\},\\ \Theta(T) &:= \{ {p}/{q}\in\operatorname{\mathbb{Q}P}^1 \mid T({p}/{q}) \text{ is thin} \}. \end{align*}
Here ![]() $T({p}/{q})$ is the
$T({p}/{q})$ is the ![]() ${p}/{q}$-rational filling of
${p}/{q}$-rational filling of ![]() $T$, that is, the link obtained by closing the tangle
$T$, that is, the link obtained by closing the tangle ![]() $T$ with a
$T$ with a ![]() ${-p}/{q}$-rational tangle, using the tangle gluing convention shown in Figure 1. We call these the A-link filling space and the thin filling space of the tangle
${-p}/{q}$-rational tangle, using the tangle gluing convention shown in Figure 1. We call these the A-link filling space and the thin filling space of the tangle ![]() $T$, respectively. Strictly speaking, we should decorate each of these with the homology theory in question; we use subscripts to do so where needed. Often, however, the four spaces
$T$, respectively. Strictly speaking, we should decorate each of these with the homology theory in question; we use subscripts to do so where needed. Often, however, the four spaces ![]() $\mathrm {A}_{\operatorname {Kh}}(T)$,
$\mathrm {A}_{\operatorname {Kh}}(T)$, ![]() $\mathrm {A}_{\operatorname {HF}}(T)$,
$\mathrm {A}_{\operatorname {HF}}(T)$, ![]() $\Theta _{\operatorname {HF}}(T)$, and
$\Theta _{\operatorname {HF}}(T)$, and ![]() $\Theta _{\operatorname {Kh}}(T)$ coincide. Moreover, the central statements in this paper hold in both the Khovanov and Heegaard Floer setting. Therefore, we do not specify the homology theory in the remainder of this introduction.
$\Theta _{\operatorname {Kh}}(T)$ coincide. Moreover, the central statements in this paper hold in both the Khovanov and Heegaard Floer setting. Therefore, we do not specify the homology theory in the remainder of this introduction.
Theorem 1.8 (Characterization of A-link filling spaces)
For any Conway tangle ![]() $T$,
$T$, ![]() $\mathrm {A}(T)$ is either empty, a single point or an interval in
$\mathrm {A}(T)$ is either empty, a single point or an interval in ![]() $\operatorname {\mathbb {Q}P}^1$.
$\operatorname {\mathbb {Q}P}^1$.

Figure 1. Two isotopic Conway tangle decompositions defining the link ![]() $T_1\cup T_2$. The tangle
$T_1\cup T_2$. The tangle ![]() $T_2$ is the result of rotating
$T_2$ is the result of rotating ![]() $T_2$ around the vertical axis. By rotating the entire link on the right-hand side around the vertical axis, we can see that
$T_2$ around the vertical axis. By rotating the entire link on the right-hand side around the vertical axis, we can see that ![]() $T_1\cup T_2=T_2\cup T_1$.
$T_1\cup T_2=T_2\cup T_1$.
Theorem 1.9 (Characterization of thin filling spaces)
For any Conway tangle ![]() $T$,
$T$, ![]() $\Theta (T)$ is either empty, a single point, two distinct points, or an interval in
$\Theta (T)$ is either empty, a single point, two distinct points, or an interval in ![]() $\operatorname {\mathbb {Q}P}^1$.
$\operatorname {\mathbb {Q}P}^1$.
Theorems 1.8 and 1.9 illustrate the difference between A-links and thin links. However, whereas Heegaard Floer A-links need not be Heegaard Floer thin, see Example 7.15, we do not know any tangle for which ![]() $\Theta (T)$ consists of two distinct points, neither in Heegaard Floer nor Khovanov theory. If such a tangle exists in Khovanov homology, then the rational fillings of this tangle include Khovanov A-links that are not Khovanov thin. In particular, this would establish that Khovanov homology does not have full support. Despite the (potential) existence of such pathological examples, we know that thin and A-link filling spaces coincide generically in the following sense.
$\Theta (T)$ consists of two distinct points, neither in Heegaard Floer nor Khovanov theory. If such a tangle exists in Khovanov homology, then the rational fillings of this tangle include Khovanov A-links that are not Khovanov thin. In particular, this would establish that Khovanov homology does not have full support. Despite the (potential) existence of such pathological examples, we know that thin and A-link filling spaces coincide generically in the following sense.
Proposition 1.10 If ![]() $\Theta (T)$ is an interval, then
$\Theta (T)$ is an interval, then ![]() $\Theta (T)=\mathrm {A}(T)$.
$\Theta (T)=\mathrm {A}(T)$.
In contrast with ![]() $\mathcal {L}(M)$, when
$\mathcal {L}(M)$, when ![]() $\mathrm {A}(T)$ or
$\mathrm {A}(T)$ or ![]() $\Theta (T)$ is an interval with two distinct boundary points the interval need not necessarily be closed. This suggests that analogues of the L-space gluing theorem have to be slightly more subtle. The proofs of all results in this paper rely on the homological invariants
$\Theta (T)$ is an interval with two distinct boundary points the interval need not necessarily be closed. This suggests that analogues of the L-space gluing theorem have to be slightly more subtle. The proofs of all results in this paper rely on the homological invariants ![]() $\operatorname {HFT}(T)$ and
$\operatorname {HFT}(T)$ and ![]() $\widetilde {\operatorname {Kh}}(T)$, which are generalizations of Heegaard Floer and Khovanov homology of links to Conway tangles [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Reference ZibrowiusZib19, Reference ZibrowiusZib20, Reference ZibrowiusZib23b]; these invariants are reviewed in §§ 3 and 5, respectively. Given two Conway tangles
$\widetilde {\operatorname {Kh}}(T)$, which are generalizations of Heegaard Floer and Khovanov homology of links to Conway tangles [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Reference ZibrowiusZib19, Reference ZibrowiusZib20, Reference ZibrowiusZib23b]; these invariants are reviewed in §§ 3 and 5, respectively. Given two Conway tangles ![]() $T_1$ and
$T_1$ and ![]() $T_2$, let
$T_2$, let ![]() $\Gamma _1$ denote the Heegaard Floer/Khovanov tangle invariant of
$\Gamma _1$ denote the Heegaard Floer/Khovanov tangle invariant of ![]() $T_1^*$, the mirror of
$T_1^*$, the mirror of ![]() $T_1$, and let
$T_1$, and let ![]() $\Gamma _2$ be the corresponding invariant of
$\Gamma _2$ be the corresponding invariant of ![]() $T_2$. The link
$T_2$. The link ![]() $T_1\cup T_2$ is obtained by identifying the two tangles according to the prescription in Figure 1.
$T_1\cup T_2$ is obtained by identifying the two tangles according to the prescription in Figure 1.
Definition 1.11 For a subset of slopes ![]() $X \in \mathbb {Q} P^1$, define its mirror as
$X \in \mathbb {Q} P^1$, define its mirror as ![]() $X^{\operatorname {m}}=\{-s\,|\, s\in X\}$.
$X^{\operatorname {m}}=\{-s\,|\, s\in X\}$.
Theorem 1.12 (A-link gluing theorem)
The link ![]() $T_1\cup T_2$ is an A-link if and only if:
$T_1\cup T_2$ is an A-link if and only if:
(1)
 $\mathrm {A}^{\operatorname {m}}(T_1) \cup \mathrm {A}(T_2) = \operatorname {\mathbb {Q}P}^1$; and
$\mathrm {A}^{\operatorname {m}}(T_1) \cup \mathrm {A}(T_2) = \operatorname {\mathbb {Q}P}^1$; and(2) certain conditions indexed by
 $\partial \mathrm {A}^{\operatorname {m}}(T_1) \cap \partial \mathrm {A}(T_2)$ hold for
$\partial \mathrm {A}^{\operatorname {m}}(T_1) \cap \partial \mathrm {A}(T_2)$ hold for  $\Gamma _1$ and
$\Gamma _1$ and  $\Gamma _2$.
$\Gamma _2$.
Condition (2) is easy to describe, once the relevant tangle invariants have been reviewed. Note that this condition is vacuously satisfied if ![]() $\partial \mathrm {A}^{\operatorname {m}}(T_1) \cap \partial \mathrm {A}(T_2) = \varnothing$, which is true generically. This allows us to obtain the following.
$\partial \mathrm {A}^{\operatorname {m}}(T_1) \cap \partial \mathrm {A}(T_2) = \varnothing$, which is true generically. This allows us to obtain the following.
Corollary 1.13 Let ![]() $\mathring {\mathrm {A}}(T_i)$ denote the interior of
$\mathring {\mathrm {A}}(T_i)$ denote the interior of ![]() $\mathrm {A}(T_i)$ for
$\mathrm {A}(T_i)$ for ![]() $i=1,2$. Then
$i=1,2$. Then
There is also an analogue of the A-link gluing theorem for thinness. However, due to the characterization results of A-link versus thin filling spaces, this analogue requires an additional hypothesis about the tangle invariants ![]() $\operatorname {HFT}(T)$ and
$\operatorname {HFT}(T)$ and ![]() $\widetilde {\operatorname {Kh}}(T)$. For this, we introduce the notion of Heegaard Floer/Khovanov exceptionality for tangles (Definitions 4.24 and 6.11). Heegaard Floer exceptional tangles do exist, see Example 7.15. We conjecture that Khovanov exceptional tangles do not exist. That such a conjecture is reasonable is supported by the following.
$\widetilde {\operatorname {Kh}}(T)$. For this, we introduce the notion of Heegaard Floer/Khovanov exceptionality for tangles (Definitions 4.24 and 6.11). Heegaard Floer exceptional tangles do exist, see Example 7.15. We conjecture that Khovanov exceptional tangles do not exist. That such a conjecture is reasonable is supported by the following.
Proposition 1.14 If a Khovanov exceptional tangle exists, then there exists a link whose Khovanov homology is supported in precisely two non-adjacent ![]() $\delta$-gradings.
$\delta$-gradings.
Once more, the question of full support is brought to the foreground.
Theorem 1.15 (Thin gluing theorem)
Suppose at most one of ![]() $T_1$ and
$T_1$ and ![]() $T_2$ is exceptional. Then
$T_2$ is exceptional. Then ![]() $T_1\cup T_2$ is thin if and only if:
$T_1\cup T_2$ is thin if and only if:
(1)
 $\Theta ^{\operatorname {m}}(T_1) \cup \Theta (T_2) = \operatorname {\mathbb {Q}P}^1$; and
$\Theta ^{\operatorname {m}}(T_1) \cup \Theta (T_2) = \operatorname {\mathbb {Q}P}^1$; and(2) certain conditions indexed by
 $\partial \Theta ^{\operatorname {m}}(T_1) \cap \partial \Theta (T_2)$ hold for
$\partial \Theta ^{\operatorname {m}}(T_1) \cap \partial \Theta (T_2)$ hold for  $\Gamma _1$ and
$\Gamma _1$ and  $\Gamma _2$.
$\Gamma _2$.
Corollary 1.16 Let ![]() $\mathring {\Theta }(T_i)$ denote the interior of
$\mathring {\Theta }(T_i)$ denote the interior of ![]() $\Theta (T_i)$ for
$\Theta (T_i)$ for ![]() $i=1,2$. Then
$i=1,2$. Then
Corollary 1.13 and Corollary 1.16 provide the condition one checks in practice. Some examples are discussed in § 7.
How to read this paper
The similarities between Heegaard Floer and Khovanov homology, highlighted by the main results of this paper, extend to the arguments that go into the proofs of these results. In fact, the arguments are so similar that they can be presented without reference to either link homology theory. This is done in § 2, which requires no specialized knowledge. We then show that both the Heegaard Floer invariant ![]() $\operatorname {HFT}(T)$ (§§ 3 and 4) and the Khovanov invariant
$\operatorname {HFT}(T)$ (§§ 3 and 4) and the Khovanov invariant ![]() $\operatorname {Kh}(T)$ (§§ 5 and 6) fit into this general framework. Section 7 discusses examples and applications of our main results, focussing primarily on thinness in Khovanov homology.
$\operatorname {Kh}(T)$ (§§ 5 and 6) fit into this general framework. Section 7 discusses examples and applications of our main results, focussing primarily on thinness in Khovanov homology.
The sections of this paper need not be read in order, and depending on the interests of the reader certain sections can be skimmed or even skipped. A flow chart of dependencies is given in Figure 2. For instance, having read this introduction, the reader may wish to turn immediately to the Examples in § 7 in order to get a sense of what one observes in nature. Section 2 is entirely combinatorial and makes no reference to any link homology theory. Sections 3 and 4 focus on knot Floer homology whereas §§ 5 and 6 focus on Khovanov homology following a similar structure: in both cases, we review the relevant tangle invariant in the first section and establish our new results in the second.

Figure 2. The paper's sections and their dependencies. Dashed arrows indicate dependencies that need only statements of results and not the machinery that arise in the proofs, so that the sections in each column may be read in isolation.
2. Abstracting the main argument
This section lays the combinatorial foundation on which the main results of this paper rely. Towards characterizing thin links and A-links without reference to a given homology theory, we find it compelling that, relative to tangle decompositions, thinness is amenable to the elementary combinatorial abstraction described in the following.
2.1 Combinatorics of slopes and lines
The space of slopes ![]() $\operatorname {\mathbb {Q}P}^1\subset \operatorname {\mathbb {R}P}^1 \cong S^1$, endowed with the subspace topology, carries a natural cyclic order: given a finite set of slopes
$\operatorname {\mathbb {Q}P}^1\subset \operatorname {\mathbb {R}P}^1 \cong S^1$, endowed with the subspace topology, carries a natural cyclic order: given a finite set of slopes ![]() $\{s_1,\ldots,s_n\}$ for some
$\{s_1,\ldots,s_n\}$ for some ![]() $n\geq 3$, we write
$n\geq 3$, we write
if the loop ![]() $[0,1]\ni t\mapsto s_1 \cdot e^{2\pi i t}\in S^1\subset \mathbb {C}$ based at
$[0,1]\ni t\mapsto s_1 \cdot e^{2\pi i t}\in S^1\subset \mathbb {C}$ based at ![]() $s_1$ meets
$s_1$ meets ![]() $s_l$ not before
$s_l$ not before ![]() $s_k$ if
$s_k$ if ![]() $k< l$; in short, we choose the counter-clockwise order, as illustrated in Figure 3. We call a tuple
$k< l$; in short, we choose the counter-clockwise order, as illustrated in Figure 3. We call a tuple ![]() $(s_1,\ldots,s_n)$ that satisfies this condition increasing. Note that
$(s_1,\ldots,s_n)$ that satisfies this condition increasing. Note that ![]() $s_n\neq s_1$ for any such tuple, unless
$s_n\neq s_1$ for any such tuple, unless ![]() $s_1=s_2=\cdots =s_n$. If the order is opposite, the tuple is called a decreasing tuple. For pairs of distinct slopes the interval notation
$s_1=s_2=\cdots =s_n$. If the order is opposite, the tuple is called a decreasing tuple. For pairs of distinct slopes the interval notation ![]() $(s_1,s_2)$ denotes the set of slopes
$(s_1,s_2)$ denotes the set of slopes ![]() $s$ for which
$s$ for which ![]() $(s_1,s,s_2)$ is increasing. As usual, square and round brackets are used to indicate the inclusion and exclusion of the interval boundaries.
$(s_1,s,s_2)$ is increasing. As usual, square and round brackets are used to indicate the inclusion and exclusion of the interval boundaries.

Figure 3. The thin interval relative to an increasing sequence of slopes ![]() $(s_1,s_2,s_3,\ldots,s_n)$.
$(s_1,s_2,s_3,\ldots,s_n)$.
Let ![]() $\operatorname {\mathfrak {C}}=\operatorname {\mathbb {Q}P}^1\times G\times \{0,1\}$ where
$\operatorname {\mathfrak {C}}=\operatorname {\mathbb {Q}P}^1\times G\times \{0,1\}$ where ![]() $G$ is either
$G$ is either ![]() $\mathbb {Z}$ or
$\mathbb {Z}$ or ![]() $\mathbb {Z}/2$. When it is necessary to make the distinction between the choice of
$\mathbb {Z}/2$. When it is necessary to make the distinction between the choice of ![]() $G$, we will write
$G$, we will write ![]() $\operatorname {\mathfrak {C}}=\operatorname {\mathfrak {C}_\mathit {G}}$. Elements
$\operatorname {\mathfrak {C}}=\operatorname {\mathfrak {C}_\mathit {G}}$. Elements ![]() $c\in \operatorname {\mathfrak {C}}$ will be called lines; one might represent them geometrically as slopes together with decorations in
$c\in \operatorname {\mathfrak {C}}$ will be called lines; one might represent them geometrically as slopes together with decorations in ![]() $G\times \{0,1\}$. (We choose the terminology line for distinction with curve, which will have a slightly different meaning in subsequent sections.) Given a triple
$G\times \{0,1\}$. (We choose the terminology line for distinction with curve, which will have a slightly different meaning in subsequent sections.) Given a triple ![]() $c\in \operatorname {\mathfrak {C}}$, denote the first component, the slope of
$c\in \operatorname {\mathfrak {C}}$, denote the first component, the slope of ![]() $c$, by
$c$, by ![]() $s(c)$; denote the second component, the grading of
$s(c)$; denote the second component, the grading of ![]() $c$, by
$c$, by ![]() $\operatorname {g}(c)$; the third component is denoted by
$\operatorname {g}(c)$; the third component is denoted by ![]() $\varepsilon (c)$. A line
$\varepsilon (c)$. A line ![]() $c$ is rational if
$c$ is rational if ![]() $\varepsilon (c)=0$ and special if
$\varepsilon (c)=0$ and special if ![]() $\varepsilon (c)=1$. Note that
$\varepsilon (c)=1$. Note that ![]() $G$ acts on the set
$G$ acts on the set ![]() $\operatorname {\mathfrak {C}}$, and we write
$\operatorname {\mathfrak {C}}$, and we write
Let ![]() $\operatorname {g}\colon \thinspace \operatorname {\mathfrak {C}}^2\rightarrow G$ be a function satisfying the following identities for all
$\operatorname {g}\colon \thinspace \operatorname {\mathfrak {C}}^2\rightarrow G$ be a function satisfying the following identities for all ![]() $c,c',c''\in \operatorname {\mathfrak {C}}$:
$c,c',c''\in \operatorname {\mathfrak {C}}$:
 $$\begin{gather} \operatorname{g}(c,c')+\operatorname{g}(c',c) =\begin{cases} 0 & \text{if } s(c)=s(c')\\ -1 & \text{otherwise;} \end{cases} \end{gather}$$
$$\begin{gather} \operatorname{g}(c,c')+\operatorname{g}(c',c) =\begin{cases} 0 & \text{if } s(c)=s(c')\\ -1 & \text{otherwise;} \end{cases} \end{gather}$$ A finite non-empty collection of lines ![]() $C = \{c_1,\ldots,c_n\}\subset \operatorname {\mathfrak {C}}$ is called a line set. We call
$C = \{c_1,\ldots,c_n\}\subset \operatorname {\mathfrak {C}}$ is called a line set. We call ![]() $C$
$C$ ![]() $s$-rational if
$s$-rational if ![]() $\varepsilon (c)=0$ for all
$\varepsilon (c)=0$ for all ![]() $\{c\in C\,|\,s(c)=s\}$, and
$\{c\in C\,|\,s(c)=s\}$, and ![]() $s$-special if
$s$-special if ![]() $\varepsilon (c)=1$ for all
$\varepsilon (c)=1$ for all ![]() $\{ c\in C \,|\, s(c)=s\}$.
$\{ c\in C \,|\, s(c)=s\}$.
It is often useful to consider the underlying slopes realized by a given line set ![]() $C$ in the projection
$C$ in the projection ![]() $\operatorname {\mathfrak {C}}\to \operatorname {\mathbb {Q}P}^1$. For this purpose, we define the set of supporting slopes as
$\operatorname {\mathfrak {C}}\to \operatorname {\mathbb {Q}P}^1$. For this purpose, we define the set of supporting slopes as
We call a line set ![]() $C$ trivial if all its lines are special and concentrated in a single slope; in other words, if
$C$ trivial if all its lines are special and concentrated in a single slope; in other words, if ![]() $\operatorname {\mathcal {S}}_C=\{s\}$ for some slope
$\operatorname {\mathcal {S}}_C=\{s\}$ for some slope ![]() $s\in \operatorname {\mathbb {Q}P}^1$, and
$s\in \operatorname {\mathbb {Q}P}^1$, and ![]() $C$ is
$C$ is ![]() $s$-special. Otherwise, we call
$s$-special. Otherwise, we call ![]() $C$ non-trivial.
$C$ non-trivial.
Note that the quotient homomorphism ![]() $\mathbb {Z}\rightarrow \mathbb {Z}/2$ induces a canonical map
$\mathbb {Z}\rightarrow \mathbb {Z}/2$ induces a canonical map ![]() $\operatorname {\mathfrak {C}_{\mathbb {Z}}}\rightarrow \operatorname {\mathfrak {C}_{\mathbb {Z}/2}}$, which allows us to relate lines and line sets with respect to the two choices of
$\operatorname {\mathfrak {C}_{\mathbb {Z}}}\rightarrow \operatorname {\mathfrak {C}_{\mathbb {Z}/2}}$, which allows us to relate lines and line sets with respect to the two choices of ![]() $G$. Specifically, the image of a line set
$G$. Specifically, the image of a line set ![]() $C\subset \operatorname {\mathfrak {C}_{\mathbb {Z}}}$ under this map is a multi-set; after removing any duplicate elements, we obtain a line set in
$C\subset \operatorname {\mathfrak {C}_{\mathbb {Z}}}$ under this map is a multi-set; after removing any duplicate elements, we obtain a line set in ![]() $\operatorname {\mathfrak {C}_{\mathbb {Z}/2}}$, which, by abuse of notation, we also denote by
$\operatorname {\mathfrak {C}_{\mathbb {Z}/2}}$, which, by abuse of notation, we also denote by ![]() $C$.
$C$.
Remark 2.1 In §§ 4 and 6, we construct the function ![]() $\operatorname {g}$ with the desired properties in the Heegaard Floer and the Khovanov setting, respectively. However, it is not hard to see that such a function exists and that it is essentially unique. For this, it is useful to think of
$\operatorname {g}$ with the desired properties in the Heegaard Floer and the Khovanov setting, respectively. However, it is not hard to see that such a function exists and that it is essentially unique. For this, it is useful to think of ![]() $\operatorname {\mathfrak {C}_{\mathbb {Z}}}$ in terms of a covering space of
$\operatorname {\mathfrak {C}_{\mathbb {Z}}}$ in terms of a covering space of ![]() $\operatorname {\mathbb {Q}P}^1$. More precisely, we can identify
$\operatorname {\mathbb {Q}P}^1$. More precisely, we can identify ![]() $\operatorname {\mathfrak {C}}_0:= \operatorname {\mathbb {Q}P}^1\times \mathbb {Z}\times \{0\}\subseteq \operatorname {\mathfrak {C}_{\mathbb {Z}}}$ with the pullback of the universal cover
$\operatorname {\mathfrak {C}}_0:= \operatorname {\mathbb {Q}P}^1\times \mathbb {Z}\times \{0\}\subseteq \operatorname {\mathfrak {C}_{\mathbb {Z}}}$ with the pullback of the universal cover ![]() $p\colon \thinspace \mathbb {R}\rightarrow \operatorname {\mathbb {R}P}^1$ along the inclusion
$p\colon \thinspace \mathbb {R}\rightarrow \operatorname {\mathbb {R}P}^1$ along the inclusion ![]() $\operatorname {\mathbb {Q}P}^1\hookrightarrow \operatorname {\mathbb {R}P}^1$. This is done as follows: to define a map
$\operatorname {\mathbb {Q}P}^1\hookrightarrow \operatorname {\mathbb {R}P}^1$. This is done as follows: to define a map ![]() $\eta \colon \thinspace \operatorname {\mathfrak {C}}_0\rightarrow \mathbb {R}$, fix some
$\eta \colon \thinspace \operatorname {\mathfrak {C}}_0\rightarrow \mathbb {R}$, fix some ![]() $c_\ast \in \operatorname {\mathfrak {C}}_0$ as a basepoint and define
$c_\ast \in \operatorname {\mathfrak {C}}_0$ as a basepoint and define ![]() $\eta (c_\ast )$ to be some point
$\eta (c_\ast )$ to be some point ![]() $x_\ast \in p^{-1}(s(c_\ast ))$. For each
$x_\ast \in p^{-1}(s(c_\ast ))$. For each ![]() $s\in \operatorname {\mathbb {Q}P}^1\smallsetminus \{s(c_\ast )\}$, there is some element
$s\in \operatorname {\mathbb {Q}P}^1\smallsetminus \{s(c_\ast )\}$, there is some element ![]() $c_s\in \operatorname {\mathfrak {C}}_0$ of slope
$c_s\in \operatorname {\mathfrak {C}}_0$ of slope ![]() $s$ such that
$s$ such that ![]() $\operatorname {g}(c_\ast,c_s)=0$. Let
$\operatorname {g}(c_\ast,c_s)=0$. Let ![]() $\gamma _s$ be an injective path from
$\gamma _s$ be an injective path from ![]() $s(c_\ast )$ to
$s(c_\ast )$ to ![]() $s$ which goes in counter-clockwise direction. Define
$s$ which goes in counter-clockwise direction. Define ![]() $\eta (c_s)$ as the endpoint of the lift of
$\eta (c_s)$ as the endpoint of the lift of ![]() $\gamma _s$ starting at
$\gamma _s$ starting at ![]() $x_\ast$. Then extend
$x_\ast$. Then extend ![]() $\eta$ equivariantly using the action of
$\eta$ equivariantly using the action of ![]() $G=\mathbb {Z}$ on
$G=\mathbb {Z}$ on ![]() $\operatorname {\mathfrak {C}}_0$ and the action by deck transformations on
$\operatorname {\mathfrak {C}}_0$ and the action by deck transformations on ![]() $\mathbb {R}$, where
$\mathbb {R}$, where ![]() $+1$ corresponds to a counter-clockwise loop based at
$+1$ corresponds to a counter-clockwise loop based at ![]() $c_\ast$. Under this identification of
$c_\ast$. Under this identification of ![]() $\operatorname {\mathfrak {C}}_0$ with a subspace of
$\operatorname {\mathfrak {C}}_0$ with a subspace of ![]() $\mathbb {R}$, the function
$\mathbb {R}$, the function ![]() $\operatorname {g}$ is simply the floor function of the signed distance:
$\operatorname {g}$ is simply the floor function of the signed distance:
By taking the product with ![]() $\{0,1\}$, one can easily extend this construction to
$\{0,1\}$, one can easily extend this construction to ![]() $\operatorname {\mathfrak {C}}$. For
$\operatorname {\mathfrak {C}}$. For ![]() $\operatorname {\mathfrak {C}_{\mathbb {Z}/2}}$, a similar interpretation is possible: we simply replace the universal cover of
$\operatorname {\mathfrak {C}_{\mathbb {Z}/2}}$, a similar interpretation is possible: we simply replace the universal cover of ![]() $\operatorname {\mathbb {R}P}^1$ by the connected two-fold cover.
$\operatorname {\mathbb {R}P}^1$ by the connected two-fold cover.
Although the expression for the function ![]() $\operatorname {g}$ in Remark 2.1 is very concise, we do not make any further use of this perspective. Instead, we only use the properties of the function
$\operatorname {g}$ in Remark 2.1 is very concise, we do not make any further use of this perspective. Instead, we only use the properties of the function ![]() $\operatorname {g}$, in particular the symmetry and transitivity property.
$\operatorname {g}$, in particular the symmetry and transitivity property.
Definition 2.2 Given ![]() $s\in \operatorname {\mathbb {Q}P}^1$, a line set
$s\in \operatorname {\mathbb {Q}P}^1$, a line set ![]() $C$ is called
$C$ is called ![]() $s$-consistent if
$s$-consistent if ![]() $\operatorname {g}(c,c')=0$ for all
$\operatorname {g}(c,c')=0$ for all ![]() $c,c'\in C$ with
$c,c'\in C$ with ![]() $s(c)=s=s(c')$.
$s(c)=s=s(c')$.
Note that if ![]() $C$ contains a unique line
$C$ contains a unique line ![]() $c$ for which
$c$ for which ![]() $s(c)=s$ (or, indeed, if
$s(c)=s$ (or, indeed, if ![]() $s\notin \operatorname {\mathcal {S}}_C$), then it is
$s\notin \operatorname {\mathcal {S}}_C$), then it is ![]() $s$-consistent. Thus, in particular, this is a condition that is relevant when multiple lines project to the same slope. In fact, if
$s$-consistent. Thus, in particular, this is a condition that is relevant when multiple lines project to the same slope. In fact, if ![]() $C$ is
$C$ is ![]() $s$-consistent there are at most two lines of slope
$s$-consistent there are at most two lines of slope ![]() $s$ in
$s$ in ![]() $C$, since
$C$, since ![]() $C\subset \operatorname {\mathfrak {C}}$. We relax this point of view and allow multi-sets when discussing curves in the Heegaard Floer and Khovanov settings in later sections.
$C\subset \operatorname {\mathfrak {C}}$. We relax this point of view and allow multi-sets when discussing curves in the Heegaard Floer and Khovanov settings in later sections.
Definition 2.3 We call a pair ![]() $(C,D)$ of line sets thin, or, more precisely,
$(C,D)$ of line sets thin, or, more precisely, ![]() $\boldsymbol {G}$-thin, if there exists some constant
$\boldsymbol {G}$-thin, if there exists some constant ![]() $n\in G$ such that for all
$n\in G$ such that for all ![]() $(c,d)\in C\times D$,
$(c,d)\in C\times D$,
 \[ \begin{cases} (\varepsilon(c),\varepsilon(d))\in\{(0,1),(1,0)\} & \text{if } s(c)= s(d),\\ \operatorname{g}(c,d)=n & \text{otherwise.} \end{cases} \]
\[ \begin{cases} (\varepsilon(c),\varepsilon(d))\in\{(0,1),(1,0)\} & \text{if } s(c)= s(d),\\ \operatorname{g}(c,d)=n & \text{otherwise.} \end{cases} \]
Note that if ![]() $(C,D)$ is thin, then so is
$(C,D)$ is thin, then so is ![]() $(D,C)$. For any line set
$(D,C)$. For any line set ![]() $C$, we define
$C$, we define
We write ![]() $\Theta$ in place of
$\Theta$ in place of ![]() $\Theta _G$ when the statements are true for both
$\Theta _G$ when the statements are true for both ![]() $G=\mathbb {Z}$ and
$G=\mathbb {Z}$ and ![]() $G=\mathbb {Z}/2$ or when this group is clear from the context.
$G=\mathbb {Z}/2$ or when this group is clear from the context.
Lemma 2.4 Given a line set ![]() $C$,
$C$, ![]() $s(c)\not \in \Theta (C)$ for every rational
$s(c)\not \in \Theta (C)$ for every rational ![]() $c\in C$.
$c\in C$.
Proof. This is an immediate consequence of the definitions.
Lemma 2.5 Given a line set ![]() $C$, suppose
$C$, suppose ![]() $s_0\in \Theta (C)$. Then
$s_0\in \Theta (C)$. Then ![]() $C$ is
$C$ is ![]() $s$-consistent for all slopes
$s$-consistent for all slopes ![]() $s\in \operatorname {\mathbb {Q}P}^1\smallsetminus \{s_0\}$.
$s\in \operatorname {\mathbb {Q}P}^1\smallsetminus \{s_0\}$.
Proof. Let us write ![]() $c_0=(s_0,0,0)$. Since
$c_0=(s_0,0,0)$. Since ![]() $s_0\in \Theta (C)$,
$s_0\in \Theta (C)$, ![]() $\operatorname {g}(c_0,c)=\operatorname {g}(c_0,c')$ for any lines
$\operatorname {g}(c_0,c)=\operatorname {g}(c_0,c')$ for any lines ![]() $c,c'\in C$ of slopes different from
$c,c'\in C$ of slopes different from ![]() $s_0$. In particular, this holds for lines
$s_0$. In particular, this holds for lines ![]() $c,c'$ of the same slope
$c,c'$ of the same slope ![]() $s\neq s_0$. In this case, the triple
$s\neq s_0$. In this case, the triple ![]() $(c_0,c,c')$ is increasing, so by (transitivity) of the function
$(c_0,c,c')$ is increasing, so by (transitivity) of the function ![]() $\operatorname {g}$,
$\operatorname {g}$, ![]() $\operatorname {g}(c,c')=0$.
$\operatorname {g}(c,c')=0$.
When ![]() $\operatorname {\mathcal {S}}_C$ is a singleton, there are four cases that arise for the set
$\operatorname {\mathcal {S}}_C$ is a singleton, there are four cases that arise for the set ![]() $\Theta (C)$ depending on consistency and the values of
$\Theta (C)$ depending on consistency and the values of ![]() $\varepsilon$. These are recorded in the following lemma.
$\varepsilon$. These are recorded in the following lemma.
Lemma 2.6 Given a line set ![]() $C$, suppose
$C$, suppose ![]() $\operatorname {\mathcal {S}}_C=\{s\}$ for some
$\operatorname {\mathcal {S}}_C=\{s\}$ for some ![]() $s\in \operatorname {\mathbb {Q}P}^1$. Then
$s\in \operatorname {\mathbb {Q}P}^1$. Then
 \[ \Theta(C)=\begin{cases} \{s\} & \text{if C is not s-consistent and s-special,}\\ \operatorname{\mathbb{Q}P}^1 & \text{if C is s-consistent and s-special,}\\ \varnothing & \text{if C is not s-consistent and not s-special,}\\ \operatorname{\mathbb{Q}P}^1\smallsetminus\{s\} & \text{if C is s-consistent and not s-special.} \end{cases} \]
\[ \Theta(C)=\begin{cases} \{s\} & \text{if C is not s-consistent and s-special,}\\ \operatorname{\mathbb{Q}P}^1 & \text{if C is s-consistent and s-special,}\\ \varnothing & \text{if C is not s-consistent and not s-special,}\\ \operatorname{\mathbb{Q}P}^1\smallsetminus\{s\} & \text{if C is s-consistent and not s-special.} \end{cases} \]
Proof. Suppose ![]() $C$ is not
$C$ is not ![]() $s$-consistent so that there exist
$s$-consistent so that there exist ![]() $c,c'\in C$ such that
$c,c'\in C$ such that ![]() $\operatorname {g}(c,c')\neq 0$. Now consider some ‘test’ slope
$\operatorname {g}(c,c')\neq 0$. Now consider some ‘test’ slope ![]() $s_0\neq s$ and let
$s_0\neq s$ and let ![]() $c_0=(s_0,0,0)$. The triple
$c_0=(s_0,0,0)$. The triple ![]() $(c_0,c,c')$ is increasing, so by (transitivity)
$(c_0,c,c')$ is increasing, so by (transitivity) ![]() $\operatorname {g}(c_0,c)\ne \operatorname {g}(c_0,c')$. Thus,
$\operatorname {g}(c_0,c)\ne \operatorname {g}(c_0,c')$. Thus, ![]() $s_0\notin \Theta (C)$ and
$s_0\notin \Theta (C)$ and ![]() $\Theta (C)\subseteq \{s\}$. Similarly, if
$\Theta (C)\subseteq \{s\}$. Similarly, if ![]() $C$ is
$C$ is ![]() $s$-consistent, (transitivity) implies
$s$-consistent, (transitivity) implies ![]() $\operatorname {\mathbb {Q}P}^1\smallsetminus \{s\}\subseteq \Theta (T)$. Finally, appealing to Lemma 2.4,
$\operatorname {\mathbb {Q}P}^1\smallsetminus \{s\}\subseteq \Theta (T)$. Finally, appealing to Lemma 2.4, ![]() $s\in \Theta (C)$ if and only if all lines
$s\in \Theta (C)$ if and only if all lines ![]() $c\in C$ are special.
$c\in C$ are special.
More generally, for a generic line set ![]() $C$ the set
$C$ the set ![]() $\Theta (C)$ is an interval in
$\Theta (C)$ is an interval in ![]() $\operatorname {\mathbb {Q}P}^1$, whenever it is non-empty. This behaviour can be characterized precisely as follows.
$\operatorname {\mathbb {Q}P}^1$, whenever it is non-empty. This behaviour can be characterized precisely as follows.
Lemma 2.7 Given a line set ![]() $C=\{c_1,\ldots,c_n\}$ write
$C=\{c_1,\ldots,c_n\}$ write ![]() $s_i=s(c_i)$ and suppose
$s_i=s(c_i)$ and suppose ![]() $(s_1,\ldots,s_n)$ is increasing with
$(s_1,\ldots,s_n)$ is increasing with ![]() $s_1\neq s_n$; see Figure 3. Then the following conditions are equivalent:
$s_1\neq s_n$; see Figure 3. Then the following conditions are equivalent:
(1) there exists some
 $s\in \Theta (C)$ with
$s\in \Theta (C)$ with  $s\in (s_n,s_1)$;
$s\in (s_n,s_1)$;(2)
 $\operatorname {g}(c_i,c_j)=0$ for all
$\operatorname {g}(c_i,c_j)=0$ for all  $i< j$;
$i< j$;(3)
 $(s_n,s_1)\subseteq \Theta (C)\subseteq [s_n,s_1]$;
$(s_n,s_1)\subseteq \Theta (C)\subseteq [s_n,s_1]$;(4)
 $(s_n,s_1)\subseteq \Theta (C)$.
$(s_n,s_1)\subseteq \Theta (C)$.
Proof. The implications ![]() $(3)\Rightarrow (4)\Rightarrow (1)$ are obvious. Moreover, the implication
$(3)\Rightarrow (4)\Rightarrow (1)$ are obvious. Moreover, the implication ![]() $(1)\Rightarrow (2)$ follows from (transitivity) of the function
$(1)\Rightarrow (2)$ follows from (transitivity) of the function ![]() $\operatorname {g}$, as in the proof of Lemma 2.5. Thus, it suffices to show
$\operatorname {g}$, as in the proof of Lemma 2.5. Thus, it suffices to show ![]() $(2)\Rightarrow (3)$. If part (2) holds, then, by (transitivity),
$(2)\Rightarrow (3)$. If part (2) holds, then, by (transitivity), ![]() $\operatorname {g}((s',0,0),c_i)$ is constant for all
$\operatorname {g}((s',0,0),c_i)$ is constant for all ![]() $s'\in (s_n,s_1)$, so
$s'\in (s_n,s_1)$, so ![]() $(s_n,s_1)\subseteq \Theta (C)$. Moreover, since
$(s_n,s_1)\subseteq \Theta (C)$. Moreover, since ![]() $s_1$ and
$s_1$ and ![]() $s_n$ differ
$s_n$ differ
by (symmetry) of the function ![]() $\operatorname {g}$. Then, for any
$\operatorname {g}$. Then, for any ![]() $s'\in (s_1,s_n)$,
$s'\in (s_1,s_n)$,
and, hence, ![]() $\Theta (C)\cap (s_1,s_n)=\varnothing$. This establishes part (3).
$\Theta (C)\cap (s_1,s_n)=\varnothing$. This establishes part (3).
Taken together, Lemmas 2.6 and 2.7 capture nearly all of the behaviour that is possible.
Lemma 2.8 With the same notation as in Lemma 2.7, suppose ![]() $|\operatorname {\mathcal {S}}_C|>2$ and
$|\operatorname {\mathcal {S}}_C|>2$ and ![]() $\Theta (C)\subseteq \operatorname {\mathcal {S}}_C$. Then
$\Theta (C)\subseteq \operatorname {\mathcal {S}}_C$. Then ![]() $\Theta (C)\subseteq \{s_i\}$ for some
$\Theta (C)\subseteq \{s_i\}$ for some ![]() $i$.
$i$.
Proof. Suppose there exist two distinct slopes ![]() $s,s'\in \Theta (C)$. Then by Lemma 2.5,
$s,s'\in \Theta (C)$. Then by Lemma 2.5, ![]() $C$ is
$C$ is ![]() $t$-consistent for all
$t$-consistent for all ![]() $t\in \operatorname {\mathcal {S}}_C$. Since
$t\in \operatorname {\mathcal {S}}_C$. Since ![]() $|\operatorname {\mathcal {S}}_C|>2$, we may assume that, after potentially reindexing the lines, the slopes
$|\operatorname {\mathcal {S}}_C|>2$, we may assume that, after potentially reindexing the lines, the slopes ![]() $s_1=s$,
$s_1=s$, ![]() $s_i=s'$, and
$s_i=s'$, and ![]() $s_n$ are pairwise distinct, that
$s_n$ are pairwise distinct, that ![]() $(s_1,\ldots,s_n)$ is increasing, and that
$(s_1,\ldots,s_n)$ is increasing, and that ![]() $s_{i-1}\neq s_i$. Let
$s_{i-1}\neq s_i$. Let ![]() $j$ be minimal such that
$j$ be minimal such that ![]() $s_j\neq s$. Then,
$s_j\neq s$. Then, ![]() $\operatorname {g}(c_k,c_\ell )=0$ for all
$\operatorname {g}(c_k,c_\ell )=0$ for all ![]() $j\leq k<\ell \leq n$, since
$j\leq k<\ell \leq n$, since ![]() $s\in \Theta (C)$. In particular,
$s\in \Theta (C)$. In particular, ![]() $\operatorname {g}(c_j,c_n)=0$. Since also
$\operatorname {g}(c_j,c_n)=0$. Since also ![]() $s_i\in \Theta (C)$, we get, in addition, that
$s_i\in \Theta (C)$, we get, in addition, that ![]() $\operatorname {g}(c_n,c_k)=0$ for all
$\operatorname {g}(c_n,c_k)=0$ for all ![]() $1\leq k< i$. This contradicts (symmetry) of the function
$1\leq k< i$. This contradicts (symmetry) of the function ![]() $\operatorname {g}$ unless
$\operatorname {g}$ unless ![]() $i=j$. However, if
$i=j$. However, if ![]() $i=j$, then
$i=j$, then ![]() $(s,s')\subset \Theta (C)$ by the direction
$(s,s')\subset \Theta (C)$ by the direction ![]() $(2)\Rightarrow (4)$ of Lemma 2.7, contradicting our initial assumption about
$(2)\Rightarrow (4)$ of Lemma 2.7, contradicting our initial assumption about ![]() $\Theta (C)$.
$\Theta (C)$.
Therefore, continuing with our observation preceding Lemma 2.8, the only additional case that needs special attention is ![]() $|\operatorname {\mathcal {S}}_C|=2$. We can now collect all of the forgoing into a clean statement:
$|\operatorname {\mathcal {S}}_C|=2$. We can now collect all of the forgoing into a clean statement:
Theorem 2.9 (Characterization of  $G$-thin filling spaces)
$G$-thin filling spaces)
Let ![]() $C$ be a non-trivial line set. Then
$C$ be a non-trivial line set. Then ![]() $\Theta (C)$ is either empty, a single point, two distinct points, or an interval in
$\Theta (C)$ is either empty, a single point, two distinct points, or an interval in ![]() $\operatorname {\mathbb {Q}P}^1$. For
$\operatorname {\mathbb {Q}P}^1$. For ![]() $\Theta _{\mathbb {Z}/2}(C)$, the third case does not arise.
$\Theta _{\mathbb {Z}/2}(C)$, the third case does not arise.
Observation 2.10 We have ![]() $\partial \Theta (C)\subseteq \operatorname {\mathcal {S}}_C$ for any line set
$\partial \Theta (C)\subseteq \operatorname {\mathcal {S}}_C$ for any line set ![]() $C$ by Lemmas 2.6 and 2.7. Moreover, if
$C$ by Lemmas 2.6 and 2.7. Moreover, if ![]() $C$ is non-trivial,
$C$ is non-trivial, ![]() $\operatorname {\mathcal {S}}_C$ is disjoint from the interior of
$\operatorname {\mathcal {S}}_C$ is disjoint from the interior of ![]() $\Theta (C)$.
$\Theta (C)$.
Proof of Theorem 2.9 If ![]() $|\operatorname {\mathcal {S}}_C|=1$, both statements follow from Lemma 2.6. Thus, we can assume in the following that
$|\operatorname {\mathcal {S}}_C|=1$, both statements follow from Lemma 2.6. Thus, we can assume in the following that ![]() $|\operatorname {\mathcal {S}}_C|\geq 2$. Let us also assume that
$|\operatorname {\mathcal {S}}_C|\geq 2$. Let us also assume that ![]() $\Theta (C)$ contains some slope
$\Theta (C)$ contains some slope ![]() $s$. If
$s$. If ![]() $s\not \in \operatorname {\mathcal {S}}_C$ then
$s\not \in \operatorname {\mathcal {S}}_C$ then ![]() $\Theta (C)$ is an interval by Lemma 2.7. If
$\Theta (C)$ is an interval by Lemma 2.7. If ![]() $\Theta (C)\subseteq \operatorname {\mathcal {S}}_C$ and
$\Theta (C)\subseteq \operatorname {\mathcal {S}}_C$ and ![]() $|\operatorname {\mathcal {S}}_C|>2$, the set
$|\operatorname {\mathcal {S}}_C|>2$, the set ![]() $\Theta (C)$ contains at most one slope by Lemma 2.8. This concludes the proof of the first statement. Suppose
$\Theta (C)$ contains at most one slope by Lemma 2.8. This concludes the proof of the first statement. Suppose ![]() $|\Theta _{\mathbb {Z}/2}(C)|=2$, say
$|\Theta _{\mathbb {Z}/2}(C)|=2$, say ![]() $\Theta _{\mathbb {Z}/2}(C)=\{s,s'\}$ for some distinct
$\Theta _{\mathbb {Z}/2}(C)=\{s,s'\}$ for some distinct ![]() $s,s'\in \operatorname {\mathbb {Q}P}^1$. By Lemma 2.8,
$s,s'\in \operatorname {\mathbb {Q}P}^1$. By Lemma 2.8, ![]() $\operatorname {\mathcal {S}}_C=\{s,s'\}$. By Lemma 2.5,
$\operatorname {\mathcal {S}}_C=\{s,s'\}$. By Lemma 2.5, ![]() $C$ is
$C$ is ![]() $s$- and
$s$- and ![]() $s'$-consistent. Then, modulo 2, either
$s'$-consistent. Then, modulo 2, either ![]() $\operatorname {g}(c,c')=0$ or
$\operatorname {g}(c,c')=0$ or ![]() $\operatorname {g}(c',c)=0$ for any two lines
$\operatorname {g}(c',c)=0$ for any two lines ![]() $c,c'\in C$ with
$c,c'\in C$ with ![]() $s(c)=s$ and
$s(c)=s$ and ![]() $s(c')=s'$. Thus, condition (2) of Lemma 2.7 is met, and thus
$s(c')=s'$. Thus, condition (2) of Lemma 2.7 is met, and thus ![]() $\Theta _{\mathbb {Z}/2}(C)$ is a (closed) interval, contradicting our initial assumption.
$\Theta _{\mathbb {Z}/2}(C)$ is a (closed) interval, contradicting our initial assumption.
In the generic situation, the difference between ![]() $G=\mathbb {Z}$ and
$G=\mathbb {Z}$ and ![]() $G=\mathbb {Z}/2$ vanishes.
$G=\mathbb {Z}/2$ vanishes.
Proposition 2.11 If ![]() $\Theta _{\mathbb {Z}}(C)$ is an interval,
$\Theta _{\mathbb {Z}}(C)$ is an interval, ![]() $\Theta _{\mathbb {Z}}(C)=\Theta _{\mathbb {Z}/2}(C)$.
$\Theta _{\mathbb {Z}}(C)=\Theta _{\mathbb {Z}/2}(C)$.
Proof. If ![]() $|\operatorname {\mathcal {S}}_C|=1$, this follows from the observation that a line set is
$|\operatorname {\mathcal {S}}_C|=1$, this follows from the observation that a line set is ![]() $s$-consistent with respect to
$s$-consistent with respect to ![]() $G=\mathbb {Z}/2$ if it is
$G=\mathbb {Z}/2$ if it is ![]() $s$-consistent with respect to
$s$-consistent with respect to ![]() $G=\mathbb {Z}$. If
$G=\mathbb {Z}$. If ![]() $|\operatorname {\mathcal {S}}_C|\geq 2$ and
$|\operatorname {\mathcal {S}}_C|\geq 2$ and ![]() $\Theta _{\mathbb {Z}}(C)$ is an interval then by Lemma 2.7,
$\Theta _{\mathbb {Z}}(C)$ is an interval then by Lemma 2.7, ![]() $\Theta _{\mathbb {Z}/2}(C)$ is an interval with the same endpoints. Moreover, whether an endpoint is contained in
$\Theta _{\mathbb {Z}/2}(C)$ is an interval with the same endpoints. Moreover, whether an endpoint is contained in ![]() $\Theta _G(C)$ is independent of
$\Theta _G(C)$ is independent of ![]() $G$.
$G$.
2.2 Characterizing thin pairs of line sets
We now turn to a characterization of thinness. Before stating the main theorem of this subsection, we discuss a certain exceptional class of line sets which requires special care, but which in the Heegaard Floer and Khovanov settings is ultimately a pathology that we have not observed in practice.
Definition 2.12 We call a line set ![]() $C$ exceptional if
$C$ exceptional if ![]() $\operatorname {\mathcal {S}}_C=\{s,s'\}$ for distinct slopes
$\operatorname {\mathcal {S}}_C=\{s,s'\}$ for distinct slopes ![]() $s,s'\in \operatorname {\mathbb {Q}P}^1$,
$s,s'\in \operatorname {\mathbb {Q}P}^1$, ![]() $C$ is
$C$ is ![]() $s$- and
$s$- and ![]() $s'$-consistent, but there are lines
$s'$-consistent, but there are lines ![]() $c,c'\in C$ with
$c,c'\in C$ with ![]() $s(c)=s$ and
$s(c)=s$ and ![]() $s(c')=s'$ such that neither
$s(c')=s'$ such that neither ![]() $\operatorname {g}(c,c')$ nor
$\operatorname {g}(c,c')$ nor ![]() $\operatorname {g}(c',c)$ are equal to 0.
$\operatorname {g}(c',c)$ are equal to 0.
Note that if ![]() $G=\mathbb {Z}/2$, there do not exist exceptional line sets. In particular, we have the following result.
$G=\mathbb {Z}/2$, there do not exist exceptional line sets. In particular, we have the following result.
Proposition 2.13 If ![]() $\Theta _{\mathbb {Z}}(C)=\{s,s'\}$ with
$\Theta _{\mathbb {Z}}(C)=\{s,s'\}$ with ![]() $s\neq s'$, then
$s\neq s'$, then ![]() $\operatorname {\mathcal {S}}_C=\{s,s'\}$ and
$\operatorname {\mathcal {S}}_C=\{s,s'\}$ and ![]() $\Theta _{\mathbb {Z}/2}(C)=[s,s']$ or
$\Theta _{\mathbb {Z}/2}(C)=[s,s']$ or ![]() $[s',s]$.
$[s',s]$.
Proof. If ![]() $|\operatorname {\mathcal {S}}_C|=1$,
$|\operatorname {\mathcal {S}}_C|=1$, ![]() $|\Theta _{\mathbb {Z}}(C)|\neq 2$ by Lemma 2.6. For the case
$|\Theta _{\mathbb {Z}}(C)|\neq 2$ by Lemma 2.6. For the case ![]() $|\operatorname {\mathcal {S}}_C|\geq 2$, the statement follows from the same arguments as the proof of the second statement of Theorem 2.9.
$|\operatorname {\mathcal {S}}_C|\geq 2$, the statement follows from the same arguments as the proof of the second statement of Theorem 2.9.
Theorem 2.14  $G$-thin gluing theorem
$G$-thin gluing theorem
Let ![]() $(C,D)$ be a pair of non-trivial line sets. Suppose not both
$(C,D)$ be a pair of non-trivial line sets. Suppose not both ![]() $C$ and
$C$ and ![]() $D$ are exceptional. Then
$D$ are exceptional. Then ![]() $(C,D)$ is thin if and only if:
$(C,D)$ is thin if and only if:
(1)
 $\Theta (C) \cup \Theta (D) =\operatorname {\mathbb {Q}P}^1$; and
$\Theta (C) \cup \Theta (D) =\operatorname {\mathbb {Q}P}^1$; and(2) for all
 $s\in \partial \Theta (C)\cap \partial \Theta (D)$, at least one of
$s\in \partial \Theta (C)\cap \partial \Theta (D)$, at least one of  $C$ and
$C$ and  $D$ is
$D$ is  $s$-rational.
$s$-rational.
We first prove a technical lemma that will simplify the proof of Theorem 2.14.
Lemma 2.15 Let ![]() $(C,D)$ be a pair of non-trivial line sets. Suppose
$(C,D)$ be a pair of non-trivial line sets. Suppose ![]() $\Theta (C) \cup \Theta (D) =\operatorname {\mathbb {Q}P}^1$. Then
$\Theta (C) \cup \Theta (D) =\operatorname {\mathbb {Q}P}^1$. Then ![]() $\operatorname {\mathcal {S}}_C\cap \operatorname {\mathcal {S}}_D=\partial \Theta (C)\cap \partial \Theta (D)$.
$\operatorname {\mathcal {S}}_C\cap \operatorname {\mathcal {S}}_D=\partial \Theta (C)\cap \partial \Theta (D)$.
Proof. The inclusion ![]() $\supseteq$ follows from the first part of Observation 2.10. For the inclusion
$\supseteq$ follows from the first part of Observation 2.10. For the inclusion ![]() $\subseteq$, we distinguish four cases, depending on the size of
$\subseteq$, we distinguish four cases, depending on the size of ![]() $|\operatorname {\mathcal {S}}_C|$ and
$|\operatorname {\mathcal {S}}_C|$ and ![]() $|\operatorname {\mathcal {S}}_D|$. If
$|\operatorname {\mathcal {S}}_D|$. If ![]() $|\operatorname {\mathcal {S}}_C|=1=|\operatorname {\mathcal {S}}_D|$, either
$|\operatorname {\mathcal {S}}_C|=1=|\operatorname {\mathcal {S}}_D|$, either ![]() $\operatorname {\mathcal {S}}_C\cap \operatorname {\mathcal {S}}_D=\varnothing$, so there is nothing to show, or
$\operatorname {\mathcal {S}}_C\cap \operatorname {\mathcal {S}}_D=\varnothing$, so there is nothing to show, or ![]() $\operatorname {\mathcal {S}}_C=\{s\}=\operatorname {\mathcal {S}}_D$ for some slope
$\operatorname {\mathcal {S}}_C=\{s\}=\operatorname {\mathcal {S}}_D$ for some slope ![]() $s$, in which case
$s$, in which case ![]() $\Theta (C) \cup \Theta (D) = \operatorname {\mathbb {Q}P}^1\smallsetminus \{s\} \subsetneq \operatorname {\mathbb {Q}P}^1$ by Lemma 2.6 and the non-triviality of
$\Theta (C) \cup \Theta (D) = \operatorname {\mathbb {Q}P}^1\smallsetminus \{s\} \subsetneq \operatorname {\mathbb {Q}P}^1$ by Lemma 2.6 and the non-triviality of ![]() $C$ and
$C$ and ![]() $D$. Suppose
$D$. Suppose ![]() $|\operatorname {\mathcal {S}}_C|>1$ and
$|\operatorname {\mathcal {S}}_C|>1$ and ![]() $|\operatorname {\mathcal {S}}_D|=1$, say
$|\operatorname {\mathcal {S}}_D|=1$, say ![]() $\operatorname {\mathcal {S}}_D=\{s\}$. If
$\operatorname {\mathcal {S}}_D=\{s\}$. If ![]() $D$ is not
$D$ is not ![]() $s$-consistent, the hypothesis is not satisfied by the non-triviality of
$s$-consistent, the hypothesis is not satisfied by the non-triviality of ![]() $D$, Lemma 2.6, and Theorem 2.9. If
$D$, Lemma 2.6, and Theorem 2.9. If ![]() $D$ is
$D$ is ![]() $s$-consistent,
$s$-consistent, ![]() $\Theta (D)=\operatorname {\mathbb {Q}P}^1\smallsetminus \{s\}$ by Lemma 2.6, so in particular
$\Theta (D)=\operatorname {\mathbb {Q}P}^1\smallsetminus \{s\}$ by Lemma 2.6, so in particular ![]() $s\in \partial \Theta (D)=\operatorname {\mathcal {S}}_D$. Moreover, the hypothesis implies that
$s\in \partial \Theta (D)=\operatorname {\mathcal {S}}_D$. Moreover, the hypothesis implies that ![]() $s\in \Theta (C)$. If
$s\in \Theta (C)$. If ![]() $s\not \in \operatorname {\mathcal {S}}_C$, there is nothing to show, whereas if
$s\not \in \operatorname {\mathcal {S}}_C$, there is nothing to show, whereas if ![]() $s\in \operatorname {\mathcal {S}}_C$, then also
$s\in \operatorname {\mathcal {S}}_C$, then also ![]() $s\in \partial \Theta (C)$ by Lemma 2.7. If
$s\in \partial \Theta (C)$ by Lemma 2.7. If ![]() $|\operatorname {\mathcal {S}}_C|=1$ and
$|\operatorname {\mathcal {S}}_C|=1$ and ![]() $|\operatorname {\mathcal {S}}_D|>1$, we repeat the argument with the roles of
$|\operatorname {\mathcal {S}}_D|>1$, we repeat the argument with the roles of ![]() $C$ and
$C$ and ![]() $D$ reversed. Thus, it remains to consider the case that
$D$ reversed. Thus, it remains to consider the case that ![]() $|\operatorname {\mathcal {S}}_C|, |\operatorname {\mathcal {S}}_D|>1$. Combining Lemma 2.7 with the hypothesis shows that
$|\operatorname {\mathcal {S}}_C|, |\operatorname {\mathcal {S}}_D|>1$. Combining Lemma 2.7 with the hypothesis shows that ![]() $\Theta (C)$ and
$\Theta (C)$ and ![]() $\Theta (D)$ are two intervals. The claim now follows from the second part of Observation 2.10.
$\Theta (D)$ are two intervals. The claim now follows from the second part of Observation 2.10.
Proof of Theorem 2.14 We start with a reformulation of condition (2) on the right-hand side of the asserted equivalence. Suppose for a moment that condition (1) in Theorem 2.14 holds. Then by non-triviality of ![]() $C$ and
$C$ and ![]() $D$ and Lemma 2.15,
$D$ and Lemma 2.15, ![]() $\partial \Theta (C) \cap \partial \Theta (D) = \operatorname {\mathcal {S}}_{C}\cap \operatorname {\mathcal {S}}_{D}$. Suppose further that
$\partial \Theta (C) \cap \partial \Theta (D) = \operatorname {\mathcal {S}}_{C}\cap \operatorname {\mathcal {S}}_{D}$. Suppose further that ![]() $C$ is
$C$ is ![]() $s$-rational for some slope
$s$-rational for some slope ![]() $s$. Then
$s$. Then ![]() $s\not \in \Theta (C)$ by Lemma 2.4. Therefore,
$s\not \in \Theta (C)$ by Lemma 2.4. Therefore, ![]() $s\in \Theta (D)$ and so by the same lemma,
$s\in \Theta (D)$ and so by the same lemma, ![]() $D$ is
$D$ is ![]() $s$-special. Similarly, if
$s$-special. Similarly, if ![]() $D$ is
$D$ is ![]() $s$-rational, we can apply the same argument with reversed roles of
$s$-rational, we can apply the same argument with reversed roles of ![]() $C$ and
$C$ and ![]() $D$. It therefore suffices to show that
$D$. It therefore suffices to show that ![]() $(C,D)$ is thin if and only if:
$(C,D)$ is thin if and only if:
(1)
 $\Theta (C) \cup \Theta (D) =\operatorname {\mathbb {Q}P}^1$; and
$\Theta (C) \cup \Theta (D) =\operatorname {\mathbb {Q}P}^1$; and(2′) for all
 $s\in \operatorname {\mathcal {S}}_C\cap \operatorname {\mathcal {S}}_D$,
$s\in \operatorname {\mathcal {S}}_C\cap \operatorname {\mathcal {S}}_D$,  $C$ is
$C$ is  $s$-rational and
$s$-rational and  $D$ is
$D$ is  $s$-special or vice versa.
$s$-special or vice versa.
Clearly, ![]() $(C,D)$ being thin implies condition (2
$(C,D)$ being thin implies condition (2![]() $'$). Thus, let us assume from now on that
$'$). Thus, let us assume from now on that ![]() $C$ and
$C$ and ![]() $D$ satisfy condition (2
$D$ satisfy condition (2![]() $'$). Write
$'$). Write ![]() $C=\{c_1,\ldots,c_m\}$ and
$C=\{c_1,\ldots,c_m\}$ and ![]() $D=\{d_1,\ldots,d_n\}$ for some
$D=\{d_1,\ldots,d_n\}$ for some ![]() $m,n\geq 1$, and let
$m,n\geq 1$, and let ![]() $s_i=s(c_i)$ for
$s_i=s(c_i)$ for ![]() $i=1,\ldots,m$ and
$i=1,\ldots,m$ and ![]() $t_j=s(d_j)$ for
$t_j=s(d_j)$ for ![]() $j=1,\ldots,n$. We order the components of
$j=1,\ldots,n$. We order the components of ![]() $C$ and
$C$ and ![]() $D$ such that both
$D$ such that both ![]() $(s_1,\ldots,s_m)$ and
$(s_1,\ldots,s_m)$ and ![]() $(t_1,\ldots,t_n)$ are increasing tuples. The proof proceeds in four cases indexed by
$(t_1,\ldots,t_n)$ are increasing tuples. The proof proceeds in four cases indexed by ![]() $|\operatorname {\mathcal {S}}_C\cap \operatorname {\mathcal {S}}_D|$.
$|\operatorname {\mathcal {S}}_C\cap \operatorname {\mathcal {S}}_D|$.
Case 0: ![]() $\operatorname {\mathcal {S}}_C\cap \operatorname {\mathcal {S}}_D=\varnothing$. In this case
$\operatorname {\mathcal {S}}_C\cap \operatorname {\mathcal {S}}_D=\varnothing$. In this case ![]() $(C,D)$ is thin if and only if there exists some
$(C,D)$ is thin if and only if there exists some ![]() $M\in G$ such that
$M\in G$ such that ![]() $\operatorname {g}(c,d)=M$ for all
$\operatorname {g}(c,d)=M$ for all ![]() $(c,d)\in C\times D$. By (transitivity), this is the case if and only if after some cyclic permutation of the indices
$(c,d)\in C\times D$. By (transitivity), this is the case if and only if after some cyclic permutation of the indices
is an increasing tuple such that ![]() $\operatorname {g}(c_i,c_j)=0$ and
$\operatorname {g}(c_i,c_j)=0$ and ![]() $\operatorname {g}(d_i,d_j)=0$ for all
$\operatorname {g}(d_i,d_j)=0$ for all ![]() $i< j$. (Otherwise, if
$i< j$. (Otherwise, if ![]() $\operatorname {\mathcal {S}}_C$ and
$\operatorname {\mathcal {S}}_C$ and ![]() $\operatorname {\mathcal {S}}_D$ intertwine, in the sense that there exist
$\operatorname {\mathcal {S}}_D$ intertwine, in the sense that there exist ![]() $i,j,k,\ell$ such that
$i,j,k,\ell$ such that ![]() $(s_i,t_j,s_k,t_\ell )$ is increasing, (transitivity) implies
$(s_i,t_j,s_k,t_\ell )$ is increasing, (transitivity) implies ![]() $M=g(c_i,d_\ell )=g(c_i,d_j)+g(d_j,c_k)+g(c_k,d_\ell )=M+(-1-M)+M$, which is false.) By Lemmas 2.6 and 2.7, the latter condition is equivalent to
$M=g(c_i,d_\ell )=g(c_i,d_j)+g(d_j,c_k)+g(c_k,d_\ell )=M+(-1-M)+M$, which is false.) By Lemmas 2.6 and 2.7, the latter condition is equivalent to ![]() $\Theta (C)$ and
$\Theta (C)$ and ![]() $\Theta (D)$ being two overlapping intervals.
$\Theta (D)$ being two overlapping intervals.
Case 1: ![]() $\operatorname {\mathcal {S}}_C\cap \operatorname {\mathcal {S}}_D=\{s\}$. (a) Suppose
$\operatorname {\mathcal {S}}_C\cap \operatorname {\mathcal {S}}_D=\{s\}$. (a) Suppose ![]() $\operatorname {\mathcal {S}}_C=\operatorname {\mathcal {S}}_D=\{s\}$. Then, because neither
$\operatorname {\mathcal {S}}_C=\operatorname {\mathcal {S}}_D=\{s\}$. Then, because neither ![]() $C$ nor
$C$ nor ![]() $D$ are trivial,
$D$ are trivial, ![]() $C$ and
$C$ and ![]() $D$ each contain at least one rational line of slope
$D$ each contain at least one rational line of slope ![]() $s$. Thus,
$s$. Thus, ![]() $(C,D)$ is not thin. Moreover,
$(C,D)$ is not thin. Moreover, ![]() $s$ is neither in
$s$ is neither in ![]() $\Theta (C)$ nor in
$\Theta (C)$ nor in ![]() $\Theta (D)$, so property (1) does not hold either.
$\Theta (D)$, so property (1) does not hold either.
(b) Suppose ![]() $\operatorname {\mathcal {S}}_C=\{s\}$ and
$\operatorname {\mathcal {S}}_C=\{s\}$ and ![]() $\operatorname {\mathcal {S}}_D\supsetneq \{s\}$. If
$\operatorname {\mathcal {S}}_D\supsetneq \{s\}$. If ![]() $C$ is not
$C$ is not ![]() $s$-consistent, condition (1) is false. This is because in this case,
$s$-consistent, condition (1) is false. This is because in this case, ![]() $\Theta (C)=\varnothing$ by Lemma 2.6 and non-triviality of
$\Theta (C)=\varnothing$ by Lemma 2.6 and non-triviality of ![]() $C$, and
$C$, and ![]() $\Theta (D)\neq \operatorname {\mathbb {Q}P}^1$ by Lemma 2.7. On the other hand,
$\Theta (D)\neq \operatorname {\mathbb {Q}P}^1$ by Lemma 2.7. On the other hand, ![]() $C$ not being
$C$ not being ![]() $s$-consistent, in conjunction with (transitivity), implies that
$s$-consistent, in conjunction with (transitivity), implies that ![]() $(C,D)$ is not thin, so the equivalence holds in this case. Suppose now that
$(C,D)$ is not thin, so the equivalence holds in this case. Suppose now that ![]() $C$ is
$C$ is ![]() $s$-consistent. Then
$s$-consistent. Then ![]() $\Theta (C)=\operatorname {\mathbb {Q}P}^1\smallsetminus \{s\}$ by non-triviality of
$\Theta (C)=\operatorname {\mathbb {Q}P}^1\smallsetminus \{s\}$ by non-triviality of ![]() $C$ and Lemma 2.6. Therefore, condition (1) is equivalent to
$C$ and Lemma 2.6. Therefore, condition (1) is equivalent to ![]() $s\in \Theta (D)$. Now observe that since
$s\in \Theta (D)$. Now observe that since ![]() $C$ is non-trivial, it is not
$C$ is non-trivial, it is not ![]() $s$-special. Since we are assuming that condition (2
$s$-special. Since we are assuming that condition (2![]() $'$) holds, this implies that
$'$) holds, this implies that ![]() $C$ is
$C$ is ![]() $s$-rational and
$s$-rational and ![]() $D$ is
$D$ is ![]() $s$-special. In particular,
$s$-special. In particular, ![]() $C$ consists of a single rational line. Thus, by (linearity),
$C$ consists of a single rational line. Thus, by (linearity), ![]() $(C,D)$ is thin if and only if
$(C,D)$ is thin if and only if ![]() $((s,0,0),D)$ is thin, i.e.
$((s,0,0),D)$ is thin, i.e. ![]() $s\in \Theta (D)$.
$s\in \Theta (D)$.
(c) Suppose ![]() $\operatorname {\mathcal {S}}_C\supsetneq \{s\}$ and
$\operatorname {\mathcal {S}}_C\supsetneq \{s\}$ and ![]() $\operatorname {\mathcal {S}}_D=\{s\}$. This is the same as Case 1(b) with reversed roles of
$\operatorname {\mathcal {S}}_D=\{s\}$. This is the same as Case 1(b) with reversed roles of ![]() $C$ and
$C$ and ![]() $D$.
$D$.
(d) Suppose ![]() $|\operatorname {\mathcal {S}}_C|,|\operatorname {\mathcal {S}}_D|>1$. Let us reindex the lines such that
$|\operatorname {\mathcal {S}}_C|,|\operatorname {\mathcal {S}}_D|>1$. Let us reindex the lines such that ![]() $s_m\neq s_1=s=t_n\neq t_1$, and
$s_m\neq s_1=s=t_n\neq t_1$, and ![]() $(s_1,\ldots,s_m)$ and
$(s_1,\ldots,s_m)$ and ![]() $(t_1,\ldots,t_n)$ are increasing. After potentially interchanging
$(t_1,\ldots,t_n)$ are increasing. After potentially interchanging ![]() $C$ and
$C$ and ![]() $D$, we may assume without loss of generality that
$D$, we may assume without loss of generality that ![]() $(s,s_k,t_\ell )$ is increasing for some
$(s,s_k,t_\ell )$ is increasing for some ![]() $k,\ell$ such that
$k,\ell$ such that ![]() $s_k\neq s \neq t_\ell$. By (transitivity),
$s_k\neq s \neq t_\ell$. By (transitivity), ![]() $(C,D)$ is thin if and only if (i)
$(C,D)$ is thin if and only if (i) ![]() $(s,s_m,t_1)$ is an increasing tuple, and (ii)
$(s,s_m,t_1)$ is an increasing tuple, and (ii) ![]() $\operatorname {g}(s_i,s_j)=0$ and
$\operatorname {g}(s_i,s_j)=0$ and ![]() $\operatorname {g}(t_i,t_j)=0$ for
$\operatorname {g}(t_i,t_j)=0$ for ![]() $i< j$, or equivalently, (ii
$i< j$, or equivalently, (ii![]() $'$)
$'$) ![]() $(s,t_1)\subseteq \Theta (D)$, and
$(s,t_1)\subseteq \Theta (D)$, and ![]() $(s_m,s) \subseteq \Theta (C)$, by Lemma 2.7. Conditions (ii
$(s_m,s) \subseteq \Theta (C)$, by Lemma 2.7. Conditions (ii![]() $'$) and (2
$'$) and (2![]() $'$) imply that
$'$) imply that ![]() $s\in \Theta (D)$ or
$s\in \Theta (D)$ or ![]() $s\in \Theta (C)$. Together with condition (i), part (1) follows. Conversely, suppose conditions (1) and (2
$s\in \Theta (C)$. Together with condition (i), part (1) follows. Conversely, suppose conditions (1) and (2![]() $'$) hold. Since by Lemma 2.7,
$'$) hold. Since by Lemma 2.7, ![]() $\Theta (C)$ and
$\Theta (C)$ and ![]() $\Theta (D)$ are contained in the closures of open intervals disjoint from any supporting slopes of
$\Theta (D)$ are contained in the closures of open intervals disjoint from any supporting slopes of ![]() $C$ and
$C$ and ![]() $D$, respectively, condition (1) implies (i) and (ii
$D$, respectively, condition (1) implies (i) and (ii![]() $'$).
$'$).
Case 2: ![]() $\operatorname {\mathcal {S}}_C\cap \operatorname {\mathcal {S}}_D=\{s,t\}$. (a) Suppose
$\operatorname {\mathcal {S}}_C\cap \operatorname {\mathcal {S}}_D=\{s,t\}$. (a) Suppose ![]() $|\operatorname {\mathcal {S}}_C|=2=|\operatorname {\mathcal {S}}_D|$. Suppose further that
$|\operatorname {\mathcal {S}}_C|=2=|\operatorname {\mathcal {S}}_D|$. Suppose further that ![]() $C$ is not
$C$ is not ![]() $s$-consistent. Then
$s$-consistent. Then ![]() $\Theta (C)=\varnothing$ and, hence,
$\Theta (C)=\varnothing$ and, hence, ![]() $\Theta (C) \cup \Theta (D) \neq \operatorname {\mathbb {Q}P}^1$. Indeed,
$\Theta (C) \cup \Theta (D) \neq \operatorname {\mathbb {Q}P}^1$. Indeed, ![]() $(C,D)$ is not thin in this case. Similarly, one can show that the theorem holds whenever
$(C,D)$ is not thin in this case. Similarly, one can show that the theorem holds whenever ![]() $C$ or
$C$ or ![]() $D$ are not
$D$ are not ![]() $s$- and
$s$- and ![]() $t$-consistent. Thus, now let us assume that
$t$-consistent. Thus, now let us assume that ![]() $C$ and
$C$ and ![]() $D$ are
$D$ are ![]() $s$- and
$s$- and ![]() $t$-consistent. By the assumptions that we have already made, we can write
$t$-consistent. By the assumptions that we have already made, we can write ![]() $C=\{c,c'\}$ and
$C=\{c,c'\}$ and ![]() $D=\{d,d'\}$ where
$D=\{d,d'\}$ where ![]() $s(c)=s(d)=s$ and
$s(c)=s(d)=s$ and ![]() $s(c')=s(d')=t$. Then, by Lemma 2.7,
$s(c')=s(d')=t$. Then, by Lemma 2.7,
Now, ![]() $(C,D)$ being thin is equivalent to
$(C,D)$ being thin is equivalent to ![]() $\operatorname {g}(c,d')=\operatorname {g}(c',d)$. By (transitivity)
$\operatorname {g}(c,d')=\operatorname {g}(c',d)$. By (transitivity) ![]() $\operatorname {g}(c,d')=\operatorname {g}(c,d)+\operatorname {g}(d,d')$ and
$\operatorname {g}(c,d')=\operatorname {g}(c,d)+\operatorname {g}(d,d')$ and ![]() $\operatorname {g}(c',d)=\operatorname {g}(c',c)+\operatorname {g}(c,d)$, and so the condition
$\operatorname {g}(c',d)=\operatorname {g}(c',c)+\operatorname {g}(c,d)$, and so the condition ![]() $\operatorname {g}(c,d')=\operatorname {g}(c',d)$ is equivalent to
$\operatorname {g}(c,d')=\operatorname {g}(c',d)$ is equivalent to ![]() $\operatorname {g}(c',c)=\operatorname {g}(d,d')$. By (symmetry) of
$\operatorname {g}(c',c)=\operatorname {g}(d,d')$. By (symmetry) of ![]() $\operatorname {g}$, this is equivalent to
$\operatorname {g}$, this is equivalent to ![]() $\operatorname {g}(c,c')=\operatorname {g}(d',d)$. The latter two conditions, in conjunction with the four equivalences above, are equivalent to the condition
$\operatorname {g}(c,c')=\operatorname {g}(d',d)$. The latter two conditions, in conjunction with the four equivalences above, are equivalent to the condition ![]() $\Theta (C) \cup \Theta (D) \supseteq \operatorname {\mathbb {Q}P}^1\smallsetminus \{s,t\}$, since we are assuming that not both
$\Theta (C) \cup \Theta (D) \supseteq \operatorname {\mathbb {Q}P}^1\smallsetminus \{s,t\}$, since we are assuming that not both ![]() $C$ and
$C$ and ![]() $D$ are exceptional. This is equivalent to condition (1) since by condition (2
$D$ are exceptional. This is equivalent to condition (1) since by condition (2![]() $'$), either
$'$), either ![]() $C$ or
$C$ or ![]() $D$ is
$D$ is ![]() $s$-special and either
$s$-special and either ![]() $C$ or
$C$ or ![]() $D$ is
$D$ is ![]() $t$-special.
$t$-special.
(b) Suppose ![]() $|\operatorname {\mathcal {S}}_C|>2$. After potentially interchanging
$|\operatorname {\mathcal {S}}_C|>2$. After potentially interchanging ![]() $t$ and
$t$ and ![]() $s$, we may assume without loss of generality that
$s$, we may assume without loss of generality that ![]() $(s,s_k,t)$ is increasing for some
$(s,s_k,t)$ is increasing for some ![]() $k$ such that
$k$ such that ![]() $s\neq s_k \neq t$. As in Case 1(c), let us reindex the lines such that
$s\neq s_k \neq t$. As in Case 1(c), let us reindex the lines such that ![]() $s_m\neq s_1=s=t_n\neq t_1$, and
$s_m\neq s_1=s=t_n\neq t_1$, and ![]() $(s_1,\ldots,s_m)$ and
$(s_1,\ldots,s_m)$ and ![]() $(t_1,\ldots,t_n)$ are increasing. Then, by (transitivity),
$(t_1,\ldots,t_n)$ are increasing. Then, by (transitivity), ![]() $(C,D)$ is thin if and only if
$(C,D)$ is thin if and only if ![]() $s_m=t=t_1$ and
$s_m=t=t_1$ and ![]() $\operatorname {g}(s_i,s_j)=0$ and
$\operatorname {g}(s_i,s_j)=0$ and ![]() $\operatorname {g}(t_i,t_j)=0$ for all
$\operatorname {g}(t_i,t_j)=0$ for all ![]() $i< j$. This, in turn, is equivalent to
$i< j$. This, in turn, is equivalent to ![]() $\Theta (C) \cup \Theta (D) \supseteq \operatorname {\mathbb {Q}P}^1\smallsetminus \{s,t\}$. Now conclude as in Case 2(a).
$\Theta (C) \cup \Theta (D) \supseteq \operatorname {\mathbb {Q}P}^1\smallsetminus \{s,t\}$. Now conclude as in Case 2(a).
(c) Suppose ![]() $|\operatorname {\mathcal {S}}_D|>2$. This is the same as Case 2(b) with reversed roles of
$|\operatorname {\mathcal {S}}_D|>2$. This is the same as Case 2(b) with reversed roles of ![]() $C$ and
$C$ and ![]() $D$.
$D$.
Case 3: ![]() $|\operatorname {\mathcal {S}}_C\cap \operatorname {\mathcal {S}}_D|>2$. Say
$|\operatorname {\mathcal {S}}_C\cap \operatorname {\mathcal {S}}_D|>2$. Say ![]() $s,s',s''\in \operatorname {\mathcal {S}}_C\cap \operatorname {\mathcal {S}}_D$ are pairwise distinct slopes such that
$s,s',s''\in \operatorname {\mathcal {S}}_C\cap \operatorname {\mathcal {S}}_D$ are pairwise distinct slopes such that ![]() $(s,s',s'')$ is an increasing triple. Then there exist lines
$(s,s',s'')$ is an increasing triple. Then there exist lines ![]() $c,c',c''\in C$ and
$c,c',c''\in C$ and ![]() $d,d',d''\in D$ such that
$d,d',d''\in D$ such that ![]() $s=s(c)=s(d)$,
$s=s(c)=s(d)$, ![]() $s'=s(c')=s(d')$, and
$s'=s(c')=s(d')$, and ![]() $s''=s(c'')=s(d'')$. We claim that in this case
$s''=s(c'')=s(d'')$. We claim that in this case ![]() $(C,D)$ is not thin. Suppose
$(C,D)$ is not thin. Suppose ![]() $(C,D)$ were thin. Then
$(C,D)$ were thin. Then ![]() $\operatorname {g}(c, d')=\operatorname {g}(c,d'')$, so
$\operatorname {g}(c, d')=\operatorname {g}(c,d'')$, so ![]() $\operatorname {g}(d',d'')=0$. Cyclically permuting the variables gives
$\operatorname {g}(d',d'')=0$. Cyclically permuting the variables gives ![]() $\operatorname {g}(d'',d)=\operatorname {g}(d,d')=0$. Applying (transitivity) and (symmetry) of the function
$\operatorname {g}(d'',d)=\operatorname {g}(d,d')=0$. Applying (transitivity) and (symmetry) of the function ![]() $\operatorname {g}$, this leads to a contradiction. Now observe that
$\operatorname {g}$, this leads to a contradiction. Now observe that ![]() $\Theta (C)\cup \Theta (D)\neq \operatorname {\mathbb {Q}P}^1$ according to Lemma 2.7.
$\Theta (C)\cup \Theta (D)\neq \operatorname {\mathbb {Q}P}^1$ according to Lemma 2.7.
Given any line set ![]() $C$, let
$C$, let ![]() $\mathring {\Theta }(C)$ denote the interior of
$\mathring {\Theta }(C)$ denote the interior of ![]() $\Theta (C)$.
$\Theta (C)$.
Corollary 2.16 Let ![]() $(C,D)$ be a pair of non-trivial line sets for which
$(C,D)$ be a pair of non-trivial line sets for which ![]() $\mathring {\Theta }(C)\cup \mathring {\Theta }(D)=\operatorname {\mathbb {Q}P}^1$. Then
$\mathring {\Theta }(C)\cup \mathring {\Theta }(D)=\operatorname {\mathbb {Q}P}^1$. Then ![]() $(C,D)$ is thin.
$(C,D)$ is thin.
Proof. If ![]() $\mathring {\Theta }(C)\cup \mathring {\Theta }(D)=\operatorname {\mathbb {Q}P}^1$, then
$\mathring {\Theta }(C)\cup \mathring {\Theta }(D)=\operatorname {\mathbb {Q}P}^1$, then ![]() $\Theta (C)\cup \Theta (D)=\operatorname {\mathbb {Q}P}^1$ and
$\Theta (C)\cup \Theta (D)=\operatorname {\mathbb {Q}P}^1$ and ![]() $\partial \Theta (C)\cap \partial \Theta (D)=\varnothing$. Thus, under the assumption that not both
$\partial \Theta (C)\cap \partial \Theta (D)=\varnothing$. Thus, under the assumption that not both ![]() $C$ and
$C$ and ![]() $D$ are exceptional, the corollary follows from Theorem 2.14. However, we may drop this assumption, because the only case in the proof of Theorem 2.14 in which we use it is Case 2(a), which supposes
$D$ are exceptional, the corollary follows from Theorem 2.14. However, we may drop this assumption, because the only case in the proof of Theorem 2.14 in which we use it is Case 2(a), which supposes ![]() $|\operatorname {\mathcal {S}}_{C}\cap \operatorname {\mathcal {S}}_{D}|=2$. Here, however,
$|\operatorname {\mathcal {S}}_{C}\cap \operatorname {\mathcal {S}}_{D}|=2$. Here, however, ![]() $\operatorname {\mathcal {S}}_{C}\cap \operatorname {\mathcal {S}}_{D}=\varnothing$ by Lemma 2.15.
$\operatorname {\mathcal {S}}_{C}\cap \operatorname {\mathcal {S}}_{D}=\varnothing$ by Lemma 2.15.
This highlights what turns out to be the generic behaviour, in practice, and gives rise to a quick certification of thinness. As the proof of Theorem 2.14 indicates, the main work is in treating the behaviour at the boundaries of the relevant intervals. Indeed, the converse of Corollary 2.16 is not true as the following example illustrates.
Example 2.17 Let ![]() $C=\{c,c_\star \}$ and
$C=\{c,c_\star \}$ and ![]() $D=\{d,d_\star \}$ where
$D=\{d,d_\star \}$ where ![]() $c$ and
$c$ and ![]() $d$ are rational,
$d$ are rational, ![]() $c_\star$ and
$c_\star$ and ![]() $d_\star$ are special,
$d_\star$ are special, ![]() $s(c)=0=s(d_\star )$, and
$s(c)=0=s(d_\star )$, and ![]() $s(c_\star )=\infty =s(d)$. Let
$s(c_\star )=\infty =s(d)$. Let ![]() $\Delta _c=\operatorname {g}(c,c_\star )$ and
$\Delta _c=\operatorname {g}(c,c_\star )$ and ![]() $\Delta _d=\operatorname {g}(d,d_\star )$. Then,
$\Delta _d=\operatorname {g}(d,d_\star )$. Then,
 \[ \Theta(C)= \begin{cases} {[\infty,0)} & \text{if } \Delta_c=0,\\ (0,\infty] & \text{if } \Delta_c=-1,\\ \{\infty\} & \text{otherwise,} \end{cases} \quad\text{and}\quad \Theta(D)= \begin{cases} {[0,\infty)} & \text{if } \Delta_d=0,\\ (\infty,0] & \text{if } \Delta_d=-1,\\ \{0\} & \text{otherwise.} \end{cases} \]
\[ \Theta(C)= \begin{cases} {[\infty,0)} & \text{if } \Delta_c=0,\\ (0,\infty] & \text{if } \Delta_c=-1,\\ \{\infty\} & \text{otherwise,} \end{cases} \quad\text{and}\quad \Theta(D)= \begin{cases} {[0,\infty)} & \text{if } \Delta_d=0,\\ (\infty,0] & \text{if } \Delta_d=-1,\\ \{0\} & \text{otherwise.} \end{cases} \]
See Figure 4 for an illustration of one of those cases. Clearly, the hypothesis of Corollary 2.16 is not satisfied for any values of ![]() $\Delta _c$ and
$\Delta _c$ and ![]() $\Delta _d$. Moreover,
$\Delta _d$. Moreover,
so ![]() $(C,D)$ is thin if and only if
$(C,D)$ is thin if and only if ![]() $\Delta _c=\Delta _d$. If
$\Delta _c=\Delta _d$. If ![]() $\Delta _c\in \{0,-1\}$ or
$\Delta _c\in \{0,-1\}$ or ![]() $\Delta _d\in \{0,-1\}$, we can verify this independently using Theorem 2.14. Otherwise, both line sets are exceptional.
$\Delta _d\in \{0,-1\}$, we can verify this independently using Theorem 2.14. Otherwise, both line sets are exceptional.

Figure 4. An illustration of Example 2.17 for the case ![]() $\Delta _c=0=\Delta _d$.
$\Delta _c=0=\Delta _d$.
3. The tangle invariant  $\operatorname {HFT}$
$\operatorname {HFT}$
We review some properties of the immersed curve invariant ![]() $\operatorname {HFT}$ of Conway tangles due to the third author [Reference ZibrowiusZib20]; see also [Reference ZibrowiusZib19, Reference ZibrowiusZib23b].
$\operatorname {HFT}$ of Conway tangles due to the third author [Reference ZibrowiusZib20]; see also [Reference ZibrowiusZib19, Reference ZibrowiusZib23b].
3.1 The definition of  $\operatorname {HFT}$
$\operatorname {HFT}$
Given a Conway tangle ![]() $T$ in a three-ball
$T$ in a three-ball ![]() $B^3$, the invariant
$B^3$, the invariant ![]() $\operatorname {HFT}(T)$ takes the form of a multicurve on a four-punctured sphere
$\operatorname {HFT}(T)$ takes the form of a multicurve on a four-punctured sphere ![]() $S^2_4$, which can be naturally identified with the boundary of
$S^2_4$, which can be naturally identified with the boundary of ![]() $B^3$ minus the four tangle ends
$B^3$ minus the four tangle ends ![]() $\partial T$. Here, a multicurve is a collection of immersed curves with local systems. To make this precise: an immersed curve in
$\partial T$. Here, a multicurve is a collection of immersed curves with local systems. To make this precise: an immersed curve in ![]() $S^2_4$ is an immersion of
$S^2_4$ is an immersion of ![]() $S^1$, considered up to homotopy, that defines a primitive element of
$S^1$, considered up to homotopy, that defines a primitive element of ![]() $\pi _1(S^2_4)$, and each of these curves is decorated with a local system, i.e. an invertible matrix over
$\pi _1(S^2_4)$, and each of these curves is decorated with a local system, i.e. an invertible matrix over ![]() $\mathbb {F}$ considered up to matrix similarity. Local systems can be viewed as vector bundles up to isomorphism, where either
$\mathbb {F}$ considered up to matrix similarity. Local systems can be viewed as vector bundles up to isomorphism, where either ![]() $\mathbb {F}$ is equipped with the discrete topology or the bundle is equipped with a flat connection. We always drop local systems from our notation when they are trivial, i.e. if they are equal to the unique one-dimensional local system. Immersed curves carry a
$\mathbb {F}$ is equipped with the discrete topology or the bundle is equipped with a flat connection. We always drop local systems from our notation when they are trivial, i.e. if they are equal to the unique one-dimensional local system. Immersed curves carry a ![]() $\delta$-grading (described in § 4) and multiple parallel immersed curves in the same
$\delta$-grading (described in § 4) and multiple parallel immersed curves in the same ![]() $\delta$-grading are set to be equivalent to a single curve with a local system that is the direct sum of the individual local systems. We always assume that parallel immersed curves are bundled up this way. Finally, a multicurve is a collection of
$\delta$-grading are set to be equivalent to a single curve with a local system that is the direct sum of the individual local systems. We always assume that parallel immersed curves are bundled up this way. Finally, a multicurve is a collection of ![]() $\delta$-graded immersed curves.
$\delta$-graded immersed curves.
With this terminology in place, we can sketch the construction of ![]() $\operatorname {HFT}(T)$. It is defined in two steps; for details, see [Reference ZibrowiusZib20].
$\operatorname {HFT}(T)$. It is defined in two steps; for details, see [Reference ZibrowiusZib20].
First, one fixes a particular auxiliary parametrization of ![]() $\partial B^3\smallsetminus \partial T$ by four embedded arcs connecting the tangle ends. For example, the four gray dotted arcs in Figure 5(a) define such a parametrization for the
$\partial B^3\smallsetminus \partial T$ by four embedded arcs connecting the tangle ends. For example, the four gray dotted arcs in Figure 5(a) define such a parametrization for the ![]() $(2,-3)$-pretzel tangle. A tangle with such a parametrization can be encoded in a Heegaard diagram
$(2,-3)$-pretzel tangle. A tangle with such a parametrization can be encoded in a Heegaard diagram ![]() $(\Sigma,\boldsymbol {\alpha },\boldsymbol {\beta })$, where
$(\Sigma,\boldsymbol {\alpha },\boldsymbol {\beta })$, where ![]() $\Sigma$ is some surface with marked points. From this, one defines a relatively
$\Sigma$ is some surface with marked points. From this, one defines a relatively ![]() $\delta$-graded curvedFootnote 1 chain complex
$\delta$-graded curvedFootnote 1 chain complex ![]() $\operatorname {CFT^\partial }(T)$ over a certain fixed
$\operatorname {CFT^\partial }(T)$ over a certain fixed ![]() $\mathbb {F}$-algebra
$\mathbb {F}$-algebra ![]() $\operatorname {\mathcal {A}}^\partial$ as the multi-pointed Heegaard Floer theory of the triple
$\operatorname {\mathcal {A}}^\partial$ as the multi-pointed Heegaard Floer theory of the triple ![]() $(\Sigma,\boldsymbol {\alpha },\boldsymbol {\beta })$ (see [Reference ZibrowiusZib20, Section 2.3]), similar to Ozsváth and Szabó's link Floer homology [Reference Ozsváth and SzabóOS08]. One can show that the relatively
$(\Sigma,\boldsymbol {\alpha },\boldsymbol {\beta })$ (see [Reference ZibrowiusZib20, Section 2.3]), similar to Ozsváth and Szabó's link Floer homology [Reference Ozsváth and SzabóOS08]. One can show that the relatively ![]() $\delta$-graded chain homotopy type of
$\delta$-graded chain homotopy type of ![]() $\operatorname {CFT^\partial }(T)$ is an invariant of the tangle
$\operatorname {CFT^\partial }(T)$ is an invariant of the tangle ![]() $T$ with the chosen parametrization [Reference ZibrowiusZib20, Theorem 2.17].
$T$ with the chosen parametrization [Reference ZibrowiusZib20, Theorem 2.17].

Figure 5. A simple non-rational tangle and its Heegaard Floer tangle invariant.
The second step uses a classification result, which states that the chain homotopy classes of ![]() $\delta$-graded curved chain complexes over
$\delta$-graded curved chain complexes over ![]() $\operatorname {\mathcal {A}}^\partial$ are in one-to-one correspondence with free homotopy classes of
$\operatorname {\mathcal {A}}^\partial$ are in one-to-one correspondence with free homotopy classes of ![]() $\delta$-graded immersed multicurves on the four-punctured sphere
$\delta$-graded immersed multicurves on the four-punctured sphere ![]() $S^2_4$ (see [Reference ZibrowiusZib20, Theorem 0.4]). This correspondence uses a fixed parametrization of
$S^2_4$ (see [Reference ZibrowiusZib20, Theorem 0.4]). This correspondence uses a fixed parametrization of ![]() $S^2_4$ by four arcs, and we generally assume that the multicurves intersect this parametrization minimally. Roughly speaking, the intersection points of arcs with a multicurve correspond to generators of the according curved chain complexes and paths between those intersection points correspond to the differentials. Now,
$S^2_4$ by four arcs, and we generally assume that the multicurves intersect this parametrization minimally. Roughly speaking, the intersection points of arcs with a multicurve correspond to generators of the according curved chain complexes and paths between those intersection points correspond to the differentials. Now, ![]() $\operatorname {HFT}(T)$ is defined as the collection of relatively
$\operatorname {HFT}(T)$ is defined as the collection of relatively ![]() $\delta$-graded immersed curves on
$\delta$-graded immersed curves on ![]() $S^2_4$ corresponding to the curved complex
$S^2_4$ corresponding to the curved complex ![]() $\operatorname {CFT^\partial }(T)$. In this definition the parametrization of
$\operatorname {CFT^\partial }(T)$. In this definition the parametrization of ![]() $S^2_4$ (needed for multicurves) is identified with the parametrization of
$S^2_4$ (needed for multicurves) is identified with the parametrization of ![]() $\partial B^3\smallsetminus \partial T$ (needed for
$\partial B^3\smallsetminus \partial T$ (needed for ![]() $\operatorname {CFT^\partial }(T)$), and one can show that this identification is natural. Namely, if a tangle
$\operatorname {CFT^\partial }(T)$), and one can show that this identification is natural. Namely, if a tangle ![]() $T'$ is obtained from
$T'$ is obtained from ![]() $T$ by adding twists to the tangle ends, the complex
$T$ by adding twists to the tangle ends, the complex ![]() $\operatorname {CFT^\partial }(T')$ determines a new set of immersed curves
$\operatorname {CFT^\partial }(T')$ determines a new set of immersed curves ![]() $\operatorname {HFT}(T')$, which agrees with that obtained by twisting the immersed curves
$\operatorname {HFT}(T')$, which agrees with that obtained by twisting the immersed curves ![]() $\operatorname {HFT}(T)$ accordingly [Reference ZibrowiusZib23b, Theorem 0.2].
$\operatorname {HFT}(T)$ accordingly [Reference ZibrowiusZib23b, Theorem 0.2].
Theorem 3.1 For all ![]() $\tau \in \operatorname {Mod}(S^2_4)$,
$\tau \in \operatorname {Mod}(S^2_4)$, ![]() $\operatorname {HFT}(\tau (T)) = \tau (\operatorname {HFT}(T))$. In other words, the invariant
$\operatorname {HFT}(\tau (T)) = \tau (\operatorname {HFT}(T))$. In other words, the invariant ![]() $\operatorname {HFT}$ commutes with the action of the mapping class group of the four-punctured sphere.
$\operatorname {HFT}$ commutes with the action of the mapping class group of the four-punctured sphere.
Example 3.2 Figure 5(b) shows the four-punctured sphere ![]() $S^2_4$, drawn as the plane plus a point at infinity minus the four punctures labeled
$S^2_4$, drawn as the plane plus a point at infinity minus the four punctures labeled ![]() ${\mathsf {1}}$,
${\mathsf {1}}$, ![]() ${\mathsf {2}}$,
${\mathsf {2}}$, ![]() ${\mathsf {3}}$, and
${\mathsf {3}}$, and ![]() ${\mathsf {4}}$, together with the standard parametrization that identifies
${\mathsf {4}}$, together with the standard parametrization that identifies ![]() $S^2_4$ with
$S^2_4$ with ![]() $\partial B^3\smallsetminus \partial T$. The dashed curve along with the two immersed curves winding around the punctures form the invariant
$\partial B^3\smallsetminus \partial T$. The dashed curve along with the two immersed curves winding around the punctures form the invariant ![]() $\operatorname {HFT}(P_{2,-3})$ for the
$\operatorname {HFT}(P_{2,-3})$ for the ![]() $(2,-3)$-pretzel tangle [Reference ZibrowiusZib20, Example 2.26].
$(2,-3)$-pretzel tangle [Reference ZibrowiusZib20, Example 2.26].
Definition 3.3 A (parametrized) tangle is called rational if it is obtained from the trivial tangle ![]() by adding twists to the tangle ends.
by adding twists to the tangle ends.
The name rational tangle originated with Conway, who showed that these tangles are in one-to-one correspondence with fractions ![]() ${p}/{q}\in \operatorname {\mathbb {Q}P}^1$ (see [Reference ConwayCon70]). We denote the rational tangle corresponding to a slope
${p}/{q}\in \operatorname {\mathbb {Q}P}^1$ (see [Reference ConwayCon70]). We denote the rational tangle corresponding to a slope ![]() ${p}/{q}\in \operatorname {\mathbb {Q}P}^1$ by
${p}/{q}\in \operatorname {\mathbb {Q}P}^1$ by ![]() $Q_{p/q}$. The invariant
$Q_{p/q}$. The invariant ![]() $\operatorname {HFT}(Q_{p/q})$ consists of a single embedded curve which is the boundary of a disk embedded into
$\operatorname {HFT}(Q_{p/q})$ consists of a single embedded curve which is the boundary of a disk embedded into ![]() $B^3$ that separates the two tangle strands of
$B^3$ that separates the two tangle strands of ![]() $Q_{p/q}$ (see [Reference ZibrowiusZib20, Example 2.25]). The local system on this curve is one-dimensional. It is known that
$Q_{p/q}$ (see [Reference ZibrowiusZib20, Example 2.25]). The local system on this curve is one-dimensional. It is known that ![]() $\operatorname {HFT}$ detects rational tangles, as follows.
$\operatorname {HFT}$ detects rational tangles, as follows.
Theorem 3.4 [Reference ZibrowiusZib20, Theorem 6.2]
A tangle ![]() $T$ is rational if and only if
$T$ is rational if and only if ![]() $\operatorname {HFT}(T)$ consists of a single embedded component carrying the unique one-dimensional local system.
$\operatorname {HFT}(T)$ consists of a single embedded component carrying the unique one-dimensional local system.
3.2 A gluing theorem for  $\operatorname {HFT}$
$\operatorname {HFT}$
The invariant ![]() $\operatorname {HFT}(T)$ can be also defined via Zarev's bordered sutured Heegaard Floer theory [Reference ZarevZar09]. In this alternate construction, the curved chain complex
$\operatorname {HFT}(T)$ can be also defined via Zarev's bordered sutured Heegaard Floer theory [Reference ZarevZar09]. In this alternate construction, the curved chain complex ![]() $\operatorname {CFT^\partial }(T)$ is replaced by an a posteriori equivalent algebraic object, namely the bordered sutured type D structure associated with the tangle complement, which is equipped with a certain bordered sutured structure; see [Reference ZibrowiusZib23b, Section 5]. This perspective gives rise to the following gluing result which relates the invariant
$\operatorname {CFT^\partial }(T)$ is replaced by an a posteriori equivalent algebraic object, namely the bordered sutured type D structure associated with the tangle complement, which is equipped with a certain bordered sutured structure; see [Reference ZibrowiusZib23b, Section 5]. This perspective gives rise to the following gluing result which relates the invariant ![]() $\operatorname {HFT}$ to link Floer homology
$\operatorname {HFT}$ to link Floer homology ![]() $\operatorname {\widehat {HFL}}$ via Lagrangian Floer homology
$\operatorname {\widehat {HFL}}$ via Lagrangian Floer homology ![]() $\operatorname {HF}$. We always assume that tangles are glued as in Figure 1, and when such a decomposition exists, we write
$\operatorname {HF}$. We always assume that tangles are glued as in Figure 1, and when such a decomposition exists, we write ![]() $L=T_1\cup T_2$ for a link
$L=T_1\cup T_2$ for a link ![]() $L$ consisting of tangles
$L$ consisting of tangles ![]() $T_1$ and
$T_1$ and ![]() $T_2$. The mirror image of the link
$T_2$. The mirror image of the link ![]() $L$ is expressed as
$L$ is expressed as ![]() $L^*$; this notation extends to tangles so that diagrammatically the mirror of
$L^*$; this notation extends to tangles so that diagrammatically the mirror of ![]() $T_i$, expressed
$T_i$, expressed ![]() $T_i^*$, is obtained by interchanging over- and under-crossings. Thus,
$T_i^*$, is obtained by interchanging over- and under-crossings. Thus, ![]() $L^*=T_1^*\cup T_2^*$. (Note that the mirror
$L^*=T_1^*\cup T_2^*$. (Note that the mirror ![]() $T^*$ of a tangle is expressed as
$T^*$ of a tangle is expressed as ![]() $\operatorname {m} T$ in other papers.) Let
$\operatorname {m} T$ in other papers.) Let ![]() $V$ be a two-dimensional vector space supported in a single relative
$V$ be a two-dimensional vector space supported in a single relative ![]() $\delta$-grading.
$\delta$-grading.
Theorem 3.5 [Reference ZibrowiusZib20, Theorem 5.9]
If ![]() $L=T_1\cup T_2$, then
$L=T_1\cup T_2$, then
if the four open components of the tangles become identified to the same component and
otherwise.
In this theorem, the knot Floer homology ![]() $\operatorname {\widehat {HFK}}(L)$ should be understood as a
$\operatorname {\widehat {HFK}}(L)$ should be understood as a ![]() $\delta$-graded theory. A similar gluing theorem holds in the bigraded setting and also for link Floer homology, using a multivariate Alexander grading on the tangle invariants.
$\delta$-graded theory. A similar gluing theorem holds in the bigraded setting and also for link Floer homology, using a multivariate Alexander grading on the tangle invariants.
The Lagrangian Floer homology ![]() $\operatorname {HF}(\gamma,\gamma ')$ of two immersed curves with local systems
$\operatorname {HF}(\gamma,\gamma ')$ of two immersed curves with local systems ![]() $\gamma$ and
$\gamma$ and ![]() $\gamma '$ is a vector space generated by intersection points between the two curves [Reference Hanselman, Rasmussen and WatsonHRW24, Section 4] (see also [Reference KotelskiyKot19, Reference Kotelskiy, Watson and ZibrowiusKWZ19]). More precisely, one first arranges that the components are transverse and do not cobound immersed annuli; then,
$\gamma '$ is a vector space generated by intersection points between the two curves [Reference Hanselman, Rasmussen and WatsonHRW24, Section 4] (see also [Reference KotelskiyKot19, Reference Kotelskiy, Watson and ZibrowiusKWZ19]). More precisely, one first arranges that the components are transverse and do not cobound immersed annuli; then, ![]() $\operatorname {HF}(\gamma,\gamma ')$ is the homology of the following chain complex: for each intersection point between
$\operatorname {HF}(\gamma,\gamma ')$ is the homology of the following chain complex: for each intersection point between ![]() $\gamma$ and
$\gamma$ and ![]() $\gamma '$, there are
$\gamma '$, there are ![]() $n\cdot n'$ corresponding generators of the underlying chain module, where
$n\cdot n'$ corresponding generators of the underlying chain module, where ![]() $n$ and
$n$ and ![]() $n'$ are the dimensions of the local systems of
$n'$ are the dimensions of the local systems of ![]() $\gamma$ and
$\gamma$ and ![]() $\gamma '$, respectively. The differential is defined by counting certain bigons between these intersection points. As a consequence, the dimension of
$\gamma '$, respectively. The differential is defined by counting certain bigons between these intersection points. As a consequence, the dimension of ![]() $\operatorname {HF}(\gamma,\gamma ')$ is equal to the minimal intersection number between the two curves times the dimensions of their local systems, provided that the curves are not parallel. If the curves are parallel, the dimension of
$\operatorname {HF}(\gamma,\gamma ')$ is equal to the minimal intersection number between the two curves times the dimensions of their local systems, provided that the curves are not parallel. If the curves are parallel, the dimension of ![]() $\operatorname {HF}(\gamma,\gamma ')$ may be greater than the minimal geometric intersection number for certain choices of local systems; for details, see [Reference ZibrowiusZib20, Sections 4.5 and 4.6, in particular Theorem 4.45]. For a more explicit example, suppose
$\operatorname {HF}(\gamma,\gamma ')$ may be greater than the minimal geometric intersection number for certain choices of local systems; for details, see [Reference ZibrowiusZib20, Sections 4.5 and 4.6, in particular Theorem 4.45]. For a more explicit example, suppose ![]() $\gamma$ and
$\gamma$ and ![]() $\gamma '$ are parallel embedded curves of the same slope equipped with local systems of dimensions
$\gamma '$ are parallel embedded curves of the same slope equipped with local systems of dimensions ![]() $n$ and
$n$ and ![]() $n'$, respectively. Then,
$n'$, respectively. Then, ![]() $\dim \operatorname {HF}(\gamma,\gamma ')$ can realize any even number between 0 and
$\dim \operatorname {HF}(\gamma,\gamma ')$ can realize any even number between 0 and ![]() $2 (n \cdot n')$, depending on the local systems, even though the minimal geometric intersection number between these curves is zero. Throughout, we always assume that
$2 (n \cdot n')$, depending on the local systems, even though the minimal geometric intersection number between these curves is zero. Throughout, we always assume that ![]() $\gamma$ and
$\gamma$ and ![]() $\gamma '$ intersect minimally without cobounding immersed annuli.
$\gamma '$ intersect minimally without cobounding immersed annuli.
Definition 3.6 For a curve ![]() $\gamma$ in
$\gamma$ in ![]() $S^2_4$, its mirror
$S^2_4$, its mirror ![]() $\operatorname {m} (\gamma )$ is the image under the involution of
$\operatorname {m} (\gamma )$ is the image under the involution of ![]() $S^2_4$ that fixes the punctures and arcs and interchanges the gray and white faces from Figure 5(b).
$S^2_4$ that fixes the punctures and arcs and interchanges the gray and white faces from Figure 5(b).
In other words, the mirror is obtained by reflection in a plane containing the four punctures and the parametrizing arcs. This operation is important in relating ![]() $\operatorname {HFT}(T_1^*)$ to
$\operatorname {HFT}(T_1^*)$ to ![]() $\operatorname {HFT}(T_1)$ (see [Reference ZibrowiusZib20, Definition 5.3 and Proposition 5.4]).
$\operatorname {HFT}(T_1)$ (see [Reference ZibrowiusZib20, Definition 5.3 and Proposition 5.4]).
Lemma 3.7 For any Conway tangle ![]() $T$,
$T$, ![]() $\operatorname {HFT}(T^*)=\operatorname {m}(\operatorname {HFT}(T))$.
$\operatorname {HFT}(T^*)=\operatorname {m}(\operatorname {HFT}(T))$.
For example, because rational tangles satisfy ![]() $Q_s^*=Q_{-s}$ we have that
$Q_s^*=Q_{-s}$ we have that ![]() $\operatorname {HFT}(Q_{-s})=\operatorname {m}(\operatorname {HFT}(Q_s))$.
$\operatorname {HFT}(Q_{-s})=\operatorname {m}(\operatorname {HFT}(Q_s))$.
3.3 The geography problem for  $\operatorname {HFT}$
$\operatorname {HFT}$
Often, it is useful to lift immersed curves to a covering space of ![]() $S^2_4$, namely the plane
$S^2_4$, namely the plane ![]() $\mathbb {R}^2$ minus the integer lattice
$\mathbb {R}^2$ minus the integer lattice ![]() $\mathbb {Z}^2$. We may regard
$\mathbb {Z}^2$. We may regard ![]() $\mathbb {R}^2$ as the universal cover of the torus, and the torus as the two-fold cover of the sphere
$\mathbb {R}^2$ as the universal cover of the torus, and the torus as the two-fold cover of the sphere ![]() $S^2$ branched at four marked points; then the integer lattice
$S^2$ branched at four marked points; then the integer lattice ![]() $\mathbb {Z}^2$ is the preimage of the branch set. This covering space is illustrated in Figure 5(c), where the standard parametrization of
$\mathbb {Z}^2$ is the preimage of the branch set. This covering space is illustrated in Figure 5(c), where the standard parametrization of ![]() $S^2_4$ has been lifted to
$S^2_4$ has been lifted to ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ and the front face and its preimage under the covering map are shaded gray. This picture also includes the lifts of the curves in
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ and the front face and its preimage under the covering map are shaded gray. This picture also includes the lifts of the curves in ![]() $\operatorname {HFT}(P_{2,-3})$: The lift of the embedded (dashed) curve is a straight line of slope
$\operatorname {HFT}(P_{2,-3})$: The lift of the embedded (dashed) curve is a straight line of slope ![]() ${1}/{2}$, whereas the lifts of the two non-embedded components of
${1}/{2}$, whereas the lifts of the two non-embedded components of ![]() $\operatorname {HFT}(P_{2,-3})$ look more complicated. Remarkably, however, this example shows almost all the complexity of the immersed curves that can appear as components of
$\operatorname {HFT}(P_{2,-3})$ look more complicated. Remarkably, however, this example shows almost all the complexity of the immersed curves that can appear as components of ![]() $\operatorname {HFT}(T)$ for Conway tangles
$\operatorname {HFT}(T)$ for Conway tangles ![]() $T$.
$T$.
To understand the geography of components of ![]() $\operatorname {HFT}(T)$ for general tangles
$\operatorname {HFT}(T)$ for general tangles ![]() $T$, observe that the linear action on the covering space
$T$, observe that the linear action on the covering space ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ by
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ by ![]() $\mathit {SL}(2,\mathbb {Z})$ corresponds to Dehn twisting in
$\mathit {SL}(2,\mathbb {Z})$ corresponds to Dehn twisting in ![]() $S^2_4$ or, equivalently, adding twists to the tangle ends; for specific conventions see [Reference ZibrowiusZib23b, Observation 3.2].
$S^2_4$ or, equivalently, adding twists to the tangle ends; for specific conventions see [Reference ZibrowiusZib23b, Observation 3.2].
Definition 3.8 We call a curve in ![]() $S^2_4$ rational if its lift to
$S^2_4$ rational if its lift to ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ is a straight line of slope
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ is a straight line of slope ![]() ${p}/{q}$. We denote such a curve by
${p}/{q}$. We denote such a curve by ![]() $\mathbf {r}({p}/{q})$ if it has a trivial local system, and
$\mathbf {r}({p}/{q})$ if it has a trivial local system, and ![]() $\mathbf {r}_{X}({p}/{q})$ if it has a local system
$\mathbf {r}_{X}({p}/{q})$ if it has a local system ![]() $X$.
$X$.
We call a curve in ![]() $S^2_4$ special if, after some twisting, it is equal to the curve
$S^2_4$ special if, after some twisting, it is equal to the curve ![]() $\mathbf {s}_n(0;{\mathsf {i}},{\mathsf {j}})$ whose lift to
$\mathbf {s}_n(0;{\mathsf {i}},{\mathsf {j}})$ whose lift to ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ is shown in Figure 6. The lift of any special curve can be isotoped into an arbitrarily small neighborhood of a straight line of some rational slope
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ is shown in Figure 6. The lift of any special curve can be isotoped into an arbitrarily small neighborhood of a straight line of some rational slope ![]() ${p}/{q}\in \operatorname {\mathbb {Q}P}^1$ going through some punctures
${p}/{q}\in \operatorname {\mathbb {Q}P}^1$ going through some punctures ![]() ${\mathsf {i}}$ and
${\mathsf {i}}$ and ![]() ${\mathsf {j}}$, in which case we denote this curve by
${\mathsf {j}}$, in which case we denote this curve by ![]() $\mathbf {s}_n({p}/{q};{\mathsf {i}},{\mathsf {j}})$.
$\mathbf {s}_n({p}/{q};{\mathsf {i}},{\mathsf {j}})$.

Figure 6. The lift of the curve ![]() $\mathbf {s}_n(0;{\mathsf {i}},{\mathsf {j}})$, where
$\mathbf {s}_n(0;{\mathsf {i}},{\mathsf {j}})$, where ![]() $n\in \mathbb {N}$ and
$n\in \mathbb {N}$ and ![]() $({\mathsf {i}},{\mathsf {j}})=({\mathsf {4}},{\mathsf {1}})$ or
$({\mathsf {i}},{\mathsf {j}})=({\mathsf {4}},{\mathsf {1}})$ or ![]() $({\mathsf {2}},{\mathsf {3}})$.
$({\mathsf {2}},{\mathsf {3}})$.
The term rational is chosen because for rational tangles ![]() $\operatorname {HFT}(Q_{p/q})=\mathbf {r}({p}/{q})$. One can then show the following [Reference ZibrowiusZib23b, Theorem 0.5].
$\operatorname {HFT}(Q_{p/q})=\mathbf {r}({p}/{q})$. One can then show the following [Reference ZibrowiusZib23b, Theorem 0.5].
Theorem 3.9 For a Conway tangle ![]() $T$ the underlying curve of each component of
$T$ the underlying curve of each component of ![]() $\operatorname {HFT}(T)$ is either rational or special. Moreover, if it is special, its local system is equal to an identity matrix.
$\operatorname {HFT}(T)$ is either rational or special. Moreover, if it is special, its local system is equal to an identity matrix.
For example, we can now write ![]() $\operatorname {HFT}(P_{2,-3})$ as the union of the rational curve
$\operatorname {HFT}(P_{2,-3})$ as the union of the rational curve ![]() $\mathbf {r}({1}/{2})$ and the two special components
$\mathbf {r}({1}/{2})$ and the two special components ![]() $\mathbf {s}_1(0;{\mathsf {4}},{\mathsf {1}})$ and
$\mathbf {s}_1(0;{\mathsf {4}},{\mathsf {1}})$ and ![]() $\mathbf {s}_1(0;{\mathsf {2}},{\mathsf {3}})$. Whether rational components with non-trivial local systems appear in
$\mathbf {s}_1(0;{\mathsf {2}},{\mathsf {3}})$. Whether rational components with non-trivial local systems appear in ![]() $\operatorname {HFT}$ is currently not known. Special components for
$\operatorname {HFT}$ is currently not known. Special components for ![]() $n>1$ show up in the invariants of two-stranded pretzel tangles with more twists [Reference ZibrowiusZib20, Theorem 6.9]. Special components always come in pairs according to the following result, which is a simplified version of [Reference ZibrowiusZib23b, Theorem 0.10].
$n>1$ show up in the invariants of two-stranded pretzel tangles with more twists [Reference ZibrowiusZib20, Theorem 6.9]. Special components always come in pairs according to the following result, which is a simplified version of [Reference ZibrowiusZib23b, Theorem 0.10].
Theorem 3.10 Conjugation symmetry
Let ![]() $({\mathsf {i}}, {\mathsf {j}} , {\mathsf {k}}, {\mathsf {l}} )$ be some permutation of
$({\mathsf {i}}, {\mathsf {j}} , {\mathsf {k}}, {\mathsf {l}} )$ be some permutation of ![]() $({\mathsf {1}},{\mathsf {2}},{\mathsf {3}},{\mathsf {4}} )$ and let
$({\mathsf {1}},{\mathsf {2}},{\mathsf {3}},{\mathsf {4}} )$ and let ![]() ${p}/{q}\in \operatorname {\mathbb {Q}P}^1$. Then, for any Conway tangle
${p}/{q}\in \operatorname {\mathbb {Q}P}^1$. Then, for any Conway tangle ![]() $T$, the numbers of components
$T$, the numbers of components ![]() $\mathbf {s}_n({p}/{q};{\mathsf {i}},{\mathsf {j}})$ and
$\mathbf {s}_n({p}/{q};{\mathsf {i}},{\mathsf {j}})$ and ![]() $\mathbf {s}_n({p}/{q};{\mathsf {k}},{\mathsf {l}})$ in
$\mathbf {s}_n({p}/{q};{\mathsf {k}},{\mathsf {l}})$ in ![]() $\operatorname {HFT}(T)$ in any given
$\operatorname {HFT}(T)$ in any given ![]() $\delta$-grading agree.
$\delta$-grading agree.
There are also restrictions on rational components. The following is [Reference ZibrowiusZib20, Observation 6.1].
Lemma 3.11 Each rational component of ![]() $\operatorname {HFT}(T)$ separates the four punctures into two pairs, which agrees with how the two open components of
$\operatorname {HFT}(T)$ separates the four punctures into two pairs, which agrees with how the two open components of ![]() $T$ connect the tangle ends.
$T$ connect the tangle ends.
In analogy with § 2, given some slope ![]() $s\in \operatorname {\mathbb {Q}P}^1$, we call a multicurve
$s\in \operatorname {\mathbb {Q}P}^1$, we call a multicurve ![]() $s$-rational if it does not contain any special components of slope
$s$-rational if it does not contain any special components of slope ![]() $s$, and
$s$, and ![]() $s$-special if it does not contain any rational components of slope
$s$-special if it does not contain any rational components of slope ![]() $s$.
$s$.
4. Heegaard Floer thin fillings
We now turn our attention to gradings. Following [Reference ZibrowiusZib20, Definitions 4.28 and 5.1], the ![]() $\delta$-grading of an immersed multicurve
$\delta$-grading of an immersed multicurve ![]() $\Gamma$ is a function
$\Gamma$ is a function
where ![]() $\operatorname {\mathcal {G}}(\Gamma )$ is the set of intersection points between the four parametrizing arcs in
$\operatorname {\mathcal {G}}(\Gamma )$ is the set of intersection points between the four parametrizing arcs in ![]() $S^2_4$ and
$S^2_4$ and ![]() $\Gamma$, assuming that this intersection is minimal. The function
$\Gamma$, assuming that this intersection is minimal. The function ![]() $\delta$ is subject to the following compatibility condition: suppose
$\delta$ is subject to the following compatibility condition: suppose ![]() $x,x'\in \operatorname {\mathcal {G}}(\Gamma )$ are two intersection points such that there is a path
$x,x'\in \operatorname {\mathcal {G}}(\Gamma )$ are two intersection points such that there is a path ![]() $\psi$ on
$\psi$ on ![]() $\Gamma$ which connects
$\Gamma$ which connects ![]() $x$ to
$x$ to ![]() $x'$ without meeting any parametrizing arc (except at the endpoints). We distinguish three cases, which are illustrated in Figure 7: a path can turn left (a), can go straight across (b), or can turn right (c). Then
$x'$ without meeting any parametrizing arc (except at the endpoints). We distinguish three cases, which are illustrated in Figure 7: a path can turn left (a), can go straight across (b), or can turn right (c). Then
 \[ \delta(x')-\delta(x)= \begin{cases} \tfrac{1}{2} & \text{if the path } \psi \text{ turns left,}\\ 0 & \text{if the path } \psi \text{ goes straight across,}\\ -\tfrac{1}{2} & \text{if the path } \psi \text{ turns right.} \end{cases} \]
\[ \delta(x')-\delta(x)= \begin{cases} \tfrac{1}{2} & \text{if the path } \psi \text{ turns left,}\\ 0 & \text{if the path } \psi \text{ goes straight across,}\\ -\tfrac{1}{2} & \text{if the path } \psi \text{ turns right.} \end{cases} \]

Figure 7. Basic regions illustrating the definition of the ![]() $\delta$-grading on a single curve.
$\delta$-grading on a single curve.
Given a Conway tangle ![]() $T$, the generators of the underlying module of the invariant
$T$, the generators of the underlying module of the invariant ![]() $\operatorname {CFT^\partial }(T)$ are in one-to-one correspondence with elements of
$\operatorname {CFT^\partial }(T)$ are in one-to-one correspondence with elements of ![]() $\operatorname {\mathcal {G}}(\operatorname {HFT}(T))$. Moreover, these generators are homogeneous with respect to the
$\operatorname {\mathcal {G}}(\operatorname {HFT}(T))$. Moreover, these generators are homogeneous with respect to the ![]() $\delta$-grading, so the relative
$\delta$-grading, so the relative ![]() $\delta$-grading on
$\delta$-grading on ![]() $\operatorname {CFT^\partial }(T)$ determines the relative
$\operatorname {CFT^\partial }(T)$ determines the relative ![]() $\delta$-grading on the corresponding multicurve
$\delta$-grading on the corresponding multicurve ![]() $\operatorname {HFT}(T)$.
$\operatorname {HFT}(T)$.
Like link Floer homology, the invariant ![]() $\operatorname {HFT}$ comes with a relative bigrading. In this paper we are not concerned with the Alexander grading; our focus is exclusively on the
$\operatorname {HFT}$ comes with a relative bigrading. In this paper we are not concerned with the Alexander grading; our focus is exclusively on the ![]() $\delta$-grading. However, we note that the treatment of the grading that follows runs along similar lines to that of [Reference Lidman, Moore and ZibrowiusLMZ22] used to study the Alexander grading.
$\delta$-grading. However, we note that the treatment of the grading that follows runs along similar lines to that of [Reference Lidman, Moore and ZibrowiusLMZ22] used to study the Alexander grading.
4.1 The  $\delta$-grading of curves in the covering space
$\delta$-grading of curves in the covering space
We now develop tools that enable us to better understand the ![]() $\delta$-grading in terms of the covering space
$\delta$-grading in terms of the covering space ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ of the four-punctured sphere
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ of the four-punctured sphere ![]() $S^2_4$. In § 4.3, this allows us to reduce to the situation of § 2 and to apply the theorems from that section to
$S^2_4$. In § 4.3, this allows us to reduce to the situation of § 2 and to apply the theorems from that section to ![]() $\operatorname {HFT}$.
$\operatorname {HFT}$.
Definition 4.1 Recall that given a map ![]() $\gamma \colon \thinspace S^1\to S^2_4$, its lift to
$\gamma \colon \thinspace S^1\to S^2_4$, its lift to ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ is a map
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ is a map ![]() $\tilde {\gamma }\colon \thinspace [0,1]\to \mathbb {R}^2\smallsetminus \mathbb {Z}^2$ such that the diagram in Figure 8(a) commutes. Given a map
$\tilde {\gamma }\colon \thinspace [0,1]\to \mathbb {R}^2\smallsetminus \mathbb {Z}^2$ such that the diagram in Figure 8(a) commutes. Given a map ![]() $\gamma \colon \thinspace S^1\to S^2_4$, its infinite connected lift to
$\gamma \colon \thinspace S^1\to S^2_4$, its infinite connected lift to ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ is a map
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ is a map ![]() $\bar {\gamma }\colon \thinspace \mathbb {R} \to \mathbb {R}^2\smallsetminus \mathbb {Z}^2$ such that the diagram in Figure 8(b) commutes.
$\bar {\gamma }\colon \thinspace \mathbb {R} \to \mathbb {R}^2\smallsetminus \mathbb {Z}^2$ such that the diagram in Figure 8(b) commutes.

Figure 8. Lifts versus infinite connected lifts, used for studying curves via the planar cover. In this section we mainly use infinite connected lifts; in § 7 we use lifts nearly exclusively, but for illustration purposes the infinite connected lift is sometimes depicted as well. Note that with this nomenclature, the preimage of a curve in the cover may be called the infinite non-connected lift.
For notation, in this section any symbol decorated with a tilde ‘![]() $\sim$’ on top denotes the lift to
$\sim$’ on top denotes the lift to ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$; likewise, an overbar ‘–’ denotes the infinite connected lift. Infinite connected lifts are sometimes referred to as ‘lifts’ for simplicity, where the difference is clear from the context. In the following, we treat all points in the integer lattice as marked points (as opposed to punctures). Denote by
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$; likewise, an overbar ‘–’ denotes the infinite connected lift. Infinite connected lifts are sometimes referred to as ‘lifts’ for simplicity, where the difference is clear from the context. In the following, we treat all points in the integer lattice as marked points (as opposed to punctures). Denote by ![]() $P$ the union of the integer lattice points with the preimage of the parametrization of
$P$ the union of the integer lattice points with the preimage of the parametrization of ![]() $S^2_4$.
$S^2_4$.
Definition 4.2 Suppose ![]() $\Gamma =\{\bar {\gamma }_1,\ldots,\bar {\gamma }_n\}$ is a set of curves in
$\Gamma =\{\bar {\gamma }_1,\ldots,\bar {\gamma }_n\}$ is a set of curves in ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ avoiding the integer lattice points such that
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ avoiding the integer lattice points such that ![]() $P\cup \Gamma =P\cup \bar {\gamma }_1\cup \cdots \cup \bar {\gamma }_n$ is a planar graph whose vertices have all valence four.
$P\cup \Gamma =P\cup \bar {\gamma }_1\cup \cdots \cup \bar {\gamma }_n$ is a planar graph whose vertices have all valence four. ![]() $P\cup \Gamma$ divides the plane into polygons, which we call regions. A domain is a formal linear combination of regions. In other words, a domain is an element of
$P\cup \Gamma$ divides the plane into polygons, which we call regions. A domain is a formal linear combination of regions. In other words, a domain is an element of ![]() $H_2(\mathbb {R}^2,P\cup \Gamma )$.
$H_2(\mathbb {R}^2,P\cup \Gamma )$.
Let us fix a metric on the plane such that ![]() $P\cup \Gamma$ is geodesic and the angles at the vertices of
$P\cup \Gamma$ is geodesic and the angles at the vertices of ![]() $P$ are
$P$ are ![]() ${\pi }/{2}$. We then define the Euler measure
${\pi }/{2}$. We then define the Euler measure ![]() $e(D)$ of a domain
$e(D)$ of a domain ![]() $D$ to be
$D$ to be ![]() ${1}/{2\pi }$ times the integral over
${1}/{2\pi }$ times the integral over ![]() $D$ of the curvature of the metric.
$D$ of the curvature of the metric.
The figures in this section follow the same conventions as in [Reference ZibrowiusZib20]: we use the right-hand rule to determine the orientation of domains and the normal vector fields of ![]() $S^2_4$ and
$S^2_4$ and ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ are pointing into the page. Thus, the boundary of a region of multiplicity
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ are pointing into the page. Thus, the boundary of a region of multiplicity ![]() $+1$ is oriented clockwise.
$+1$ is oriented clockwise.
Note that the Euler measure is additive in the sense that ![]() $e(D+D')=e(D)+e(D')$ for any two domains
$e(D+D')=e(D)+e(D')$ for any two domains ![]() $D$ and
$D$ and ![]() $D'$. In practice, one computes the Euler measure of a domain
$D'$. In practice, one computes the Euler measure of a domain ![]() $D$ using the following formula, which follows from the Gauss–Bonnet theorem:
$D$ using the following formula, which follows from the Gauss–Bonnet theorem:
Definition 4.3 Given an absolutely ![]() $\delta$-graded curve
$\delta$-graded curve ![]() $\gamma$, consider two intersection points
$\gamma$, consider two intersection points ![]() $\tilde {x}$ and
$\tilde {x}$ and ![]() $\tilde {x}'$ of the lift
$\tilde {x}'$ of the lift ![]() $\bar {\gamma }$ with the integer lattice graph
$\bar {\gamma }$ with the integer lattice graph ![]() $P$. A connecting domain from
$P$. A connecting domain from ![]() $\tilde {x}$ to
$\tilde {x}$ to ![]() $\tilde {x}'$ is a domain
$\tilde {x}'$ is a domain ![]() $\varphi \in H_2(\mathbb {R}^2,P\cup \bar {\gamma })$ with the property
$\varphi \in H_2(\mathbb {R}^2,P\cup \bar {\gamma })$ with the property
Remark 4.4 For readers familiar with Heegaard Floer homology, it can be helpful to think of the curve ![]() $\bar {\gamma }$ as playing the role of a
$\bar {\gamma }$ as playing the role of a ![]() $\beta$-curve and
$\beta$-curve and ![]() $P$ playing the role of an
$P$ playing the role of an ![]() $\alpha$-curve.
$\alpha$-curve.
Lemma 4.5 For any connecting domain ![]() $\varphi$ as in Definition 4.3,
$\varphi$ as in Definition 4.3,
Proof. For the domains consisting of just the single regions shown in Figure 7, the lemma follows directly from the definition of the ![]() $\delta$-grading: the Euler measure of
$\delta$-grading: the Euler measure of ![]() $\varphi$ in these three cases is
$\varphi$ in these three cases is ![]() $\frac {1}{4}$, 0, and
$\frac {1}{4}$, 0, and ![]() $-\frac {1}{4}$, respectively. Now let us consider a general connecting domain
$-\frac {1}{4}$, respectively. Now let us consider a general connecting domain ![]() $\varphi$ from
$\varphi$ from ![]() $\tilde {x}$ to
$\tilde {x}$ to ![]() $\tilde {x}'$. By hypothesis,
$\tilde {x}'$. By hypothesis, ![]() $\partial \varphi \cap \bar {\gamma }$ is a one-chain connecting
$\partial \varphi \cap \bar {\gamma }$ is a one-chain connecting ![]() $\tilde {x}$ to
$\tilde {x}$ to ![]() $\tilde {x}'$. Let us first assume that this one-chain corresponds to a path from
$\tilde {x}'$. Let us first assume that this one-chain corresponds to a path from ![]() $\tilde {x}$ to
$\tilde {x}$ to ![]() $\tilde {x}'$. That is, either there are no cycles in the one-chain or, in the case
$\tilde {x}'$. That is, either there are no cycles in the one-chain or, in the case ![]() $\tilde {x}=\tilde {x}'$, this path is the only cycle. In this case the path can be written as the intersection of
$\tilde {x}=\tilde {x}'$, this path is the only cycle. In this case the path can be written as the intersection of ![]() $\bar {\gamma }$ with the boundary of a connecting domain
$\bar {\gamma }$ with the boundary of a connecting domain ![]() $\psi$, which is a sum of finitely many of the basic regions in Figure 7 that we have just considered. The difference
$\psi$, which is a sum of finitely many of the basic regions in Figure 7 that we have just considered. The difference ![]() $\varphi -\psi$ is a domain whose boundary lies entirely in
$\varphi -\psi$ is a domain whose boundary lies entirely in ![]() $P$, so it consists entirely of square regions and, hence, the Euler measure vanishes.
$P$, so it consists entirely of square regions and, hence, the Euler measure vanishes.
Finally, suppose the one-chain ![]() $\partial \varphi \cap \bar {\gamma }$ connecting
$\partial \varphi \cap \bar {\gamma }$ connecting ![]() $\tilde {x}$ to
$\tilde {x}$ to ![]() $\tilde {x}'$ also has cycles. Each of them is the boundary of some domain, and we claim that its Euler measure vanishes. To see this, we can apply the previous argument with
$\tilde {x}'$ also has cycles. Each of them is the boundary of some domain, and we claim that its Euler measure vanishes. To see this, we can apply the previous argument with ![]() $\tilde {x}=\tilde {x}'$ being some intersection point of this cycle with
$\tilde {x}=\tilde {x}'$ being some intersection point of this cycle with ![]() $P$ the connecting path being the whole cycle.
$P$ the connecting path being the whole cycle.
Definition 4.6 Let ![]() $\bullet$ be an intersection point between two absolutely
$\bullet$ be an intersection point between two absolutely ![]() $\delta$-graded curves
$\delta$-graded curves ![]() $\gamma$ and
$\gamma$ and ![]() $\gamma '$. Consider the lifts
$\gamma '$. Consider the lifts ![]() $\bar {\gamma }$ and
$\bar {\gamma }$ and ![]() $\bar {\gamma }'$ of these two curves, such that they intersect at a lift
$\bar {\gamma }'$ of these two curves, such that they intersect at a lift ![]() $\tilde {\bullet }$ of the intersection point
$\tilde {\bullet }$ of the intersection point ![]() $\bullet$. A connecting domain for
$\bullet$. A connecting domain for ![]() $\tilde {\bullet }$ from
$\tilde {\bullet }$ from ![]() $\bar {\gamma }$ to
$\bar {\gamma }$ to ![]() $\bar {\gamma }'$ is a domain
$\bar {\gamma }'$ is a domain ![]() $\varphi \in H_2(\mathbb {R}^2,P\cup \bar {\gamma }\cup \bar {\gamma }')$ with the property
$\varphi \in H_2(\mathbb {R}^2,P\cup \bar {\gamma }\cup \bar {\gamma }')$ with the property
Intersection points between bigraded curves can be endowed with a ![]() $\delta$-grading [Reference ZibrowiusZib20, Definition 4.40], and this can be easily calculated according to the following result.
$\delta$-grading [Reference ZibrowiusZib20, Definition 4.40], and this can be easily calculated according to the following result.
Lemma 4.7 With notation as in Definition 4.6, the ![]() $\delta$-grading of
$\delta$-grading of ![]() $\bullet$ satisfies
$\bullet$ satisfies
Observation 4.8 The domain ![]() $-\varphi$ is a connecting domain for the same intersection point
$-\varphi$ is a connecting domain for the same intersection point ![]() $\bullet$, but regarded as a generator of
$\bullet$, but regarded as a generator of ![]() $\operatorname {HF}(\gamma ',\gamma )$. Its
$\operatorname {HF}(\gamma ',\gamma )$. Its ![]() $\delta$-grading is equal to 1 minus the original
$\delta$-grading is equal to 1 minus the original ![]() $\delta$-grading:
$\delta$-grading:
Proof of Lemma 4.7 First consider the simplest case in which the domain ![]() $\varphi$ consists of a single region of multiplicity 1. Up to rotation, there are only four cases, as shown in Figure 9. The lemma then follows directly from [Reference ZibrowiusZib20, Definition 4.40], since in each of those cases, the intersection point corresponds to some algebra element
$\varphi$ consists of a single region of multiplicity 1. Up to rotation, there are only four cases, as shown in Figure 9. The lemma then follows directly from [Reference ZibrowiusZib20, Definition 4.40], since in each of those cases, the intersection point corresponds to some algebra element ![]() $a\in \operatorname {\mathcal {A}}^\partial$ and its
$a\in \operatorname {\mathcal {A}}^\partial$ and its ![]() $\delta$-grading
$\delta$-grading ![]() $\delta (a)$ is equal to
$\delta (a)$ is equal to ![]() $\tfrac {1}{2}-2e(\varphi )$ (see [Reference ZibrowiusZib20, Definitions 2.10 and 4.5]).
$\tfrac {1}{2}-2e(\varphi )$ (see [Reference ZibrowiusZib20, Definitions 2.10 and 4.5]).

Figure 9. Basic connecting domains satisfying the formula ![]() .
.
Now consider a general connecting domain ![]() $\varphi$. Then near
$\varphi$. Then near ![]() $\tilde {\bullet }$,
$\tilde {\bullet }$, ![]() $\varphi$ looks like one of the basic connecting domains
$\varphi$ looks like one of the basic connecting domains ![]() $\psi$ that we have just considered (up to adding multiples of square regions). Suppose
$\psi$ that we have just considered (up to adding multiples of square regions). Suppose ![]() $\psi$ connects
$\psi$ connects ![]() $\tilde {x}'\in \bar {\gamma }\cap P$ to
$\tilde {x}'\in \bar {\gamma }\cap P$ to ![]() $\tilde {y}'\in \bar {\gamma }'\cap P$. Then, as we have just verified,
$\tilde {y}'\in \bar {\gamma }'\cap P$. Then, as we have just verified,
Let ![]() $\psi _x$ and
$\psi _x$ and ![]() $\psi _y$ be connecting domains from
$\psi _y$ be connecting domains from ![]() $\tilde {x}$ to
$\tilde {x}$ to ![]() $\tilde {x}'$ and from
$\tilde {x}'$ and from ![]() $\tilde {y}'$ to
$\tilde {y}'$ to ![]() $\tilde {y}$, respectively. Then, by Lemma 4.5,
$\tilde {y}$, respectively. Then, by Lemma 4.5,
Combining all three relations, we see that
By construction, ![]() $\psi _x+\psi +\psi _y-\varphi$ is a sum of square regions and domains bounding closed components of
$\psi _x+\psi +\psi _y-\varphi$ is a sum of square regions and domains bounding closed components of ![]() $\bar {\gamma }$ and
$\bar {\gamma }$ and ![]() $\bar {\gamma }'$, so
$\bar {\gamma }'$, so ![]() $e(\psi _x+\psi +\psi _y)=e(\varphi )$.
$e(\psi _x+\psi +\psi _y)=e(\varphi )$.
Definition 4.9 Suppose ![]() $\bar {\gamma }_i$ is an infinite connected lift to
$\bar {\gamma }_i$ is an infinite connected lift to ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ of some absolutely
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ of some absolutely ![]() $\delta$-graded curve
$\delta$-graded curve ![]() $\gamma _i$ in
$\gamma _i$ in ![]() $S^2_4$ for
$S^2_4$ for ![]() $i=1,\ldots,n$, and let
$i=1,\ldots,n$, and let ![]() $x_i\in \operatorname {HF}(\gamma _i,\gamma _{i+1})$ be an intersection point between
$x_i\in \operatorname {HF}(\gamma _i,\gamma _{i+1})$ be an intersection point between ![]() $\gamma _{i}$ and
$\gamma _{i}$ and ![]() $\gamma _{i+1}$, where we take indices modulo
$\gamma _{i+1}$, where we take indices modulo ![]() $n$. A symmetric domain for the tuples
$n$. A symmetric domain for the tuples ![]() $(\bar {\gamma }_i)_{i=1,\ldots,n}$ and
$(\bar {\gamma }_i)_{i=1,\ldots,n}$ and ![]() $(\tilde {x}_i)_{i=1,\ldots,n}$ is a domain
$(\tilde {x}_i)_{i=1,\ldots,n}$ is a domain ![]() $\varphi$ satisfying
$\varphi$ satisfying
where, again, indices are taken modulo ![]() $n$.
$n$.
Proposition 4.10 For any connecting domain ![]() $\varphi$ as in Definition 4.9,
$\varphi$ as in Definition 4.9,
 \[ \sum_{i=1}^n \delta(x_i)=\frac{n}{2}-2 e(\varphi). \]
\[ \sum_{i=1}^n \delta(x_i)=\frac{n}{2}-2 e(\varphi). \]
Proof. For each ![]() $i=1,\ldots, n$, choose some intersection point
$i=1,\ldots, n$, choose some intersection point ![]() $\tilde {y}_i$ of
$\tilde {y}_i$ of ![]() $\bar {\gamma }_i$ with
$\bar {\gamma }_i$ with ![]() $P$. Then we can write
$P$. Then we can write ![]() $\varphi$ as a sum of
$\varphi$ as a sum of ![]() $n$ connecting domains
$n$ connecting domains ![]() $\varphi _i$ for
$\varphi _i$ for ![]() $\tilde {x}_i$ from
$\tilde {x}_i$ from ![]() $\tilde {y}_i$ to
$\tilde {y}_i$ to ![]() $\tilde {y}_{i+1}$. By Lemma 4.7,
$\tilde {y}_{i+1}$. By Lemma 4.7,
for ![]() $i=1,\ldots,n$. Taking the sum over all
$i=1,\ldots,n$. Taking the sum over all ![]() $n$ equations, we obtain the desired identity.
$n$ equations, we obtain the desired identity.
Definition 4.11 Given two intersection points ![]() $x,y\in \operatorname {HF}(\gamma,\gamma ')$ between two curves
$x,y\in \operatorname {HF}(\gamma,\gamma ')$ between two curves ![]() $\gamma$ and
$\gamma$ and ![]() $\gamma '$, a domain (or asymmetric domain) from
$\gamma '$, a domain (or asymmetric domain) from ![]() $\tilde {x}$ to
$\tilde {x}$ to ![]() $\tilde {y}$ is a domain
$\tilde {y}$ is a domain ![]() $\varphi \in H_2(\mathbb {R}^2,\bar {\gamma }\cup \bar {\gamma }')$ with the property
$\varphi \in H_2(\mathbb {R}^2,\bar {\gamma }\cup \bar {\gamma }')$ with the property
Corollary 4.12 For any domain ![]() $\varphi$ as in Definition 4.11,
$\varphi$ as in Definition 4.11,
Proof. Let us set ![]() $n=2$,
$n=2$, ![]() $\gamma _1=\gamma$,
$\gamma _1=\gamma$, ![]() $\gamma _2=\gamma '$, and
$\gamma _2=\gamma '$, and ![]() $x_1=x\in \operatorname {HF}(\gamma _1,\gamma _2)$. In addition, let
$x_1=x\in \operatorname {HF}(\gamma _1,\gamma _2)$. In addition, let ![]() $x_2$ be the intersection point
$x_2$ be the intersection point ![]() $y\in \operatorname {HF}(\gamma _1,\gamma _2)$, but regarded as an intersection point in
$y\in \operatorname {HF}(\gamma _1,\gamma _2)$, but regarded as an intersection point in ![]() $\operatorname {HF}(\gamma _2,\gamma _1)$. Then
$\operatorname {HF}(\gamma _2,\gamma _1)$. Then ![]() $\varphi$ can be interpreted as a symmetric domain from
$\varphi$ can be interpreted as a symmetric domain from ![]() $\tilde {x}_1$ to
$\tilde {x}_1$ to ![]() $\tilde {x}_2$. By Proposition 4.10, this implies that
$\tilde {x}_2$. By Proposition 4.10, this implies that ![]() $\delta (x_1)+\delta (x_2)=1-2 e(\varphi )$. By Observation 4.8,
$\delta (x_1)+\delta (x_2)=1-2 e(\varphi )$. By Observation 4.8, ![]() $\delta (x_2)=1-\delta (y)$. These two identities combined prove the claim.
$\delta (x_2)=1-\delta (y)$. These two identities combined prove the claim.
Example 4.13 If ![]() $\varphi$ is a bigon of multiplicity 1 as in Figure 10, Corollary 4.12 implies that
$\varphi$ is a bigon of multiplicity 1 as in Figure 10, Corollary 4.12 implies that ![]() $\delta (y)-\delta (x)=2e(\varphi )=1$; see also [Reference ZibrowiusZib20, Lemma 4.41].
$\delta (y)-\delta (x)=2e(\varphi )=1$; see also [Reference ZibrowiusZib20, Lemma 4.41].

Figure 10. A bigon illustrating Example 4.13; compare with Figure 15 and [Reference ZibrowiusZib20, Figure 31].
4.2 Linear curves
Definition 4.14 An immersed curve ![]() $\gamma$ in
$\gamma$ in ![]() $S^2_4$ is called linear if there exists some
$S^2_4$ is called linear if there exists some ![]() ${p}/{q}\in \operatorname {\mathbb {Q}P}^1$ such that for every open neighborhood
${p}/{q}\in \operatorname {\mathbb {Q}P}^1$ such that for every open neighborhood ![]() $U$ of
$U$ of ![]() ${p}/{q}$ in
${p}/{q}$ in ![]() $\operatorname {\mathbb {Q}P}^1$ there exists a curve
$\operatorname {\mathbb {Q}P}^1$ there exists a curve ![]() $\gamma _U$ homotopic to
$\gamma _U$ homotopic to ![]() $\gamma$ with the property that all the slopes
$\gamma$ with the property that all the slopes ![]() $\tilde {\gamma }'_U(t)$ of the lift
$\tilde {\gamma }'_U(t)$ of the lift ![]() $\tilde {\gamma }_U$ are contained in
$\tilde {\gamma }_U$ are contained in ![]() $U$. If there exists such a number
$U$. If there exists such a number ![]() ${p}/{q}\in \operatorname {\mathbb {Q}P}^1$, it is unique, and we call it the slope of
${p}/{q}\in \operatorname {\mathbb {Q}P}^1$, it is unique, and we call it the slope of ![]() $\gamma$.
$\gamma$.
If ![]() $\Gamma$ is a collection of linear curves, we denote the set of their slopes by
$\Gamma$ is a collection of linear curves, we denote the set of their slopes by ![]() $\operatorname {\mathcal {S}}_{\Gamma }$. We also say that a collection of curves
$\operatorname {\mathcal {S}}_{\Gamma }$. We also say that a collection of curves ![]() $\Gamma$ is supported on a slope if it contains a curve of that slope.
$\Gamma$ is supported on a slope if it contains a curve of that slope.
By Theorem 3.9, the invariant ![]() $\operatorname {HFT}(T)$ of any Conway tangle
$\operatorname {HFT}(T)$ of any Conway tangle ![]() $T$ consists of rational and special curves, which are linear. Thus, for the remainder of this section we restrict our attention to linear curves.
$T$ consists of rational and special curves, which are linear. Thus, for the remainder of this section we restrict our attention to linear curves.
The slope of the mirror of a linear curve ![]() $\gamma$ (see Definition 3.6) is equal to the mirror of the slope of
$\gamma$ (see Definition 3.6) is equal to the mirror of the slope of ![]() $\gamma$ (see Definition 1.11). Thus, by Lemma 3.7, mirroring operation commutes with taking the curve invariant
$\gamma$ (see Definition 1.11). Thus, by Lemma 3.7, mirroring operation commutes with taking the curve invariant ![]() $\operatorname {HFT}(-)$ and its slopes:
$\operatorname {HFT}(-)$ and its slopes:
Lemma 4.15 Let ![]() $\gamma$ be a linear curve of slope
$\gamma$ be a linear curve of slope ![]() $s\in \operatorname {\mathbb {Q}P}^1$. Then unless
$s\in \operatorname {\mathbb {Q}P}^1$. Then unless ![]() $s=0$, the images of all intersection points of
$s=0$, the images of all intersection points of ![]() $\bar {\gamma }$ with the horizontal lines of
$\bar {\gamma }$ with the horizontal lines of ![]() $P$ have the same
$P$ have the same ![]() $\delta$-grading
$\delta$-grading ![]() $\delta _{-}:= \delta _{-}(\gamma )$, and unless
$\delta _{-}:= \delta _{-}(\gamma )$, and unless ![]() $s=\infty$, the images of all intersection points of
$s=\infty$, the images of all intersection points of ![]() $\bar {\gamma }$ with the vertical lines of
$\bar {\gamma }$ with the vertical lines of ![]() $P$ have the same
$P$ have the same ![]() $\delta$-grading
$\delta$-grading ![]() $\delta _{|}:= \delta _{|}(\gamma )$. Moreover,
$\delta _{|}:= \delta _{|}(\gamma )$. Moreover,
 \[
\delta_{|}= \begin{cases}
\delta_{-}-\frac{1}{2} & \text{if } 0< s<\infty,
\\ \delta_{-}+\frac{1}{2} & \text{if } \infty< s<0. \end{cases} \]
\[
\delta_{|}= \begin{cases}
\delta_{-}-\frac{1}{2} & \text{if } 0< s<\infty,
\\ \delta_{-}+\frac{1}{2} & \text{if } \infty< s<0. \end{cases} \]
Proof. If ![]() $s\neq 0$, any two horizontal intersection points are connected via a rectangular domain, and so are any two vertical intersection points in the case
$s\neq 0$, any two horizontal intersection points are connected via a rectangular domain, and so are any two vertical intersection points in the case ![]() $s\neq \infty$. This proves the first two statements. For the third, suppose first that
$s\neq \infty$. This proves the first two statements. For the third, suppose first that ![]() $0< s<\infty$. Then we can connect any vertical intersection point to a horizontal intersection point by a triangular connecting domain of multiplicity
$0< s<\infty$. Then we can connect any vertical intersection point to a horizontal intersection point by a triangular connecting domain of multiplicity ![]() $+1$. The Euler measure is equal
$+1$. The Euler measure is equal ![]() $+\frac {1}{4}$ for any such pair of intersection points, so
$+\frac {1}{4}$ for any such pair of intersection points, so ![]() $\delta _{-}-\delta _{|}=\frac {1}{2}$ by Lemma 4.5. For
$\delta _{-}-\delta _{|}=\frac {1}{2}$ by Lemma 4.5. For ![]() $\infty < s<0$, the argument is the same except that the order of the intersection points is reversed; so in this case
$\infty < s<0$, the argument is the same except that the order of the intersection points is reversed; so in this case ![]() $\delta _{|}-\delta _{-}=\frac {1}{2}$.
$\delta _{|}-\delta _{-}=\frac {1}{2}$.
Definition 4.16 Given two linear curves ![]() $\gamma$ and
$\gamma$ and ![]() $\gamma '$ of the same slope
$\gamma '$ of the same slope ![]() $s\in \operatorname {\mathbb {Q}P}^1$, we define
$s\in \operatorname {\mathbb {Q}P}^1$, we define
 \[ \delta(\gamma,\gamma') =\begin{cases} \delta_{-}(\gamma')-\delta_{-}(\gamma) & \text{if } s\neq0 ,\\ \delta_{|}(\gamma')-\delta_{|}(\gamma) & \text{if } s\neq\infty. \end{cases} \]
\[ \delta(\gamma,\gamma') =\begin{cases} \delta_{-}(\gamma')-\delta_{-}(\gamma) & \text{if } s\neq0 ,\\ \delta_{|}(\gamma')-\delta_{|}(\gamma) & \text{if } s\neq\infty. \end{cases} \]
This is well-defined by Lemma 4.15. The two curves are said to have the same ![]() $\delta$-grading if
$\delta$-grading if ![]() $\delta (\gamma,\gamma ')=0$.
$\delta (\gamma,\gamma ')=0$.
Lemma 4.17 Given two linear curves ![]() $\gamma$ and
$\gamma$ and ![]() $\gamma '$ of different slopes
$\gamma '$ of different slopes ![]() $s,s'\in \operatorname {\mathbb {Q}P}^1$, the Lagrangian intersection theory
$s,s'\in \operatorname {\mathbb {Q}P}^1$, the Lagrangian intersection theory ![]() $\operatorname {HF}(\gamma,\gamma ')$ is supported in a single
$\operatorname {HF}(\gamma,\gamma ')$ is supported in a single ![]() $\delta$-grading, which is equal to
$\delta$-grading, which is equal to
 \[ \delta(\gamma,\gamma') := \begin{cases} \delta_{-}(\gamma')-\delta_{|}(\gamma)+\tfrac{1}{2} & \text{if } s\in(\infty,s') \text{ for } s'\in(0,\infty], \text{ or } s\in(s',\infty) \text{ for } s'\in[\infty,0), \\ \delta_{|}(\gamma')-\delta_{-}(\gamma)+\tfrac{1}{2} & \text{if } s\in(s',0) \text{ for } s'\in[0,\infty), \text{ or } s\in(0,s') \text{ for } s'\in(\infty,0], \end{cases} \]
\[ \delta(\gamma,\gamma') := \begin{cases} \delta_{-}(\gamma')-\delta_{|}(\gamma)+\tfrac{1}{2} & \text{if } s\in(\infty,s') \text{ for } s'\in(0,\infty], \text{ or } s\in(s',\infty) \text{ for } s'\in[\infty,0), \\ \delta_{|}(\gamma')-\delta_{-}(\gamma)+\tfrac{1}{2} & \text{if } s\in(s',0) \text{ for } s'\in[0,\infty), \text{ or } s\in(0,s') \text{ for } s'\in(\infty,0], \end{cases} \]
using the convention that ![]() $(\infty,\infty ):= \operatorname {\mathbb {Q}P}^1\smallsetminus \{\infty \}$ and
$(\infty,\infty ):= \operatorname {\mathbb {Q}P}^1\smallsetminus \{\infty \}$ and ![]() $(0,0):= \operatorname {\mathbb {Q}P}^1\smallsetminus \{0\}$.
$(0,0):= \operatorname {\mathbb {Q}P}^1\smallsetminus \{0\}$.
Proof. Fix an intersection point of ![]() $\bar {\gamma }$ and
$\bar {\gamma }$ and ![]() $\bar {\gamma }'$. In the first case, we can find a rectangular connecting domain for this intersection point between
$\bar {\gamma }'$. In the first case, we can find a rectangular connecting domain for this intersection point between ![]() $\bar {\gamma }$ and
$\bar {\gamma }$ and ![]() $\bar {\gamma }'$ of multiplicity
$\bar {\gamma }'$ of multiplicity ![]() $\pm 1$ which starts at a vertical intersection point of
$\pm 1$ which starts at a vertical intersection point of ![]() $\bar {\gamma }$ and ends at a horizontal intersection point of
$\bar {\gamma }$ and ends at a horizontal intersection point of ![]() $\bar {\gamma }'$; see Figures 11(a) and 11(b) for an illustration. We then use the formula from Lemma 4.7. We can argue similarly in the second case, which is illustrated in Figures 11(c) and 11(d). One can easily check that any
$\bar {\gamma }'$; see Figures 11(a) and 11(b) for an illustration. We then use the formula from Lemma 4.7. We can argue similarly in the second case, which is illustrated in Figures 11(c) and 11(d). One can easily check that any ![]() $(s,s')\in \operatorname {\mathbb {Q}P}^1\times \operatorname {\mathbb {Q}P}^1$ with
$(s,s')\in \operatorname {\mathbb {Q}P}^1\times \operatorname {\mathbb {Q}P}^1$ with ![]() $s\neq s'$ belongs to at least one of these two cases. Finally, the formula for the
$s\neq s'$ belongs to at least one of these two cases. Finally, the formula for the ![]() $\delta$-grading is obviously independent of the particular intersection point that we considered.
$\delta$-grading is obviously independent of the particular intersection point that we considered.
Corollary 4.18 (Symmetry of  $\delta$)
$\delta$)
For any two linear curves ![]() $\gamma$ and
$\gamma$ and ![]() $\gamma '$,
$\gamma '$,
 \[ \delta(\gamma,\gamma')+\delta(\gamma',\gamma)= \begin{cases} 0 & \text{if } s(\gamma)=s(\gamma'),\\ 1 & \text{if } s(\gamma)\neq s(\gamma'). \end{cases} \]
\[ \delta(\gamma,\gamma')+\delta(\gamma',\gamma)= \begin{cases} 0 & \text{if } s(\gamma)=s(\gamma'),\\ 1 & \text{if } s(\gamma)\neq s(\gamma'). \end{cases} \]
In the proof of Theorem 4.27, we relate the grading function ![]() $\operatorname {g}$ from § 2 to the negative of
$\operatorname {g}$ from § 2 to the negative of ![]() $\delta$. This explains the difference in sign between the symmetry of
$\delta$. This explains the difference in sign between the symmetry of ![]() $\delta$ compared with the (symmetry) of
$\delta$ compared with the (symmetry) of ![]() $\operatorname {g}$. Similarly, whereas the transitivity of
$\operatorname {g}$. Similarly, whereas the transitivity of ![]() $\operatorname {g}$ holds for increasing triples of slopes, we establish transitivity of
$\operatorname {g}$ holds for increasing triples of slopes, we establish transitivity of ![]() $\delta$ in terms of decreasing triples.
$\delta$ in terms of decreasing triples.
Theorem 4.19 (Transitivity of  $\delta$)
$\delta$)
For any triple ![]() $(\gamma,\gamma ',\gamma '')$ of linear curves in
$(\gamma,\gamma ',\gamma '')$ of linear curves in ![]() $S^2_4$ such that
$S^2_4$ such that ![]() $(s(\gamma ),s(\gamma '),s(\gamma ''))$ is decreasing,
$(s(\gamma ),s(\gamma '),s(\gamma ''))$ is decreasing,
Proof. If ![]() $s(\gamma )=s(\gamma ')$ or
$s(\gamma )=s(\gamma ')$ or ![]() $s(\gamma ')=s(\gamma '')$, or both, this follows from Definition 4.16 and Lemma 4.17. Thus, let us suppose the curves have pairwise different slopes. Let us consider some infinite connected lifts
$s(\gamma ')=s(\gamma '')$, or both, this follows from Definition 4.16 and Lemma 4.17. Thus, let us suppose the curves have pairwise different slopes. Let us consider some infinite connected lifts ![]() $\bar {\gamma }$,
$\bar {\gamma }$, ![]() $\bar {\gamma }'$, and
$\bar {\gamma }'$, and ![]() $\bar {\gamma }''$ of
$\bar {\gamma }''$ of ![]() $\gamma$,
$\gamma$, ![]() $\gamma '$, and
$\gamma '$, and ![]() $\gamma ''$, respectively. These lifts intersect in three points
$\gamma ''$, respectively. These lifts intersect in three points ![]() $\tilde {A}\in \bar {\gamma }\cap \bar {\gamma }'$,
$\tilde {A}\in \bar {\gamma }\cap \bar {\gamma }'$, ![]() $\tilde {B}\in \bar {\gamma }'\cap \bar {\gamma }''$, and
$\tilde {B}\in \bar {\gamma }'\cap \bar {\gamma }''$, and ![]() $\tilde {C}\in \bar {\gamma }''\cap \bar {\gamma }$. Consider a connecting domain
$\tilde {C}\in \bar {\gamma }''\cap \bar {\gamma }$. Consider a connecting domain ![]() $\varphi$ for
$\varphi$ for ![]() $\tilde {A}$ starting at some point
$\tilde {A}$ starting at some point ![]() $\tilde {x}\in \bar {\gamma }\cap P$ and ending at some point
$\tilde {x}\in \bar {\gamma }\cap P$ and ending at some point ![]() $\tilde {y}\in \bar {\gamma }'\cap P$. Then choose a connecting domain
$\tilde {y}\in \bar {\gamma }'\cap P$. Then choose a connecting domain ![]() $\varphi '$ for
$\varphi '$ for ![]() $\tilde {B}$ which starts at
$\tilde {B}$ which starts at ![]() $\tilde {y}$ and ends at some point
$\tilde {y}$ and ends at some point ![]() $\tilde {z}\in \bar {\gamma }''\cap P$. Since the slopes of these curves form a decreasing triple, the triangle
$\tilde {z}\in \bar {\gamma }''\cap P$. Since the slopes of these curves form a decreasing triple, the triangle ![]() $\Delta \tilde {A}\tilde {B}\tilde {C}$ has multiplicity
$\Delta \tilde {A}\tilde {B}\tilde {C}$ has multiplicity ![]() $-1$ when the vertices are ordered counter-clockwise, as illustrated in Figure 11(e); therefore,
$-1$ when the vertices are ordered counter-clockwise, as illustrated in Figure 11(e); therefore, ![]() $e(\Delta \tilde {A}\tilde {B}\tilde {C})=-\frac {1}{4}$. Thus,
$e(\Delta \tilde {A}\tilde {B}\tilde {C})=-\frac {1}{4}$. Thus, ![]() $\varphi +\varphi '+\Delta \tilde {A}\tilde {B}\tilde {C}$ is a connecting domain for
$\varphi +\varphi '+\Delta \tilde {A}\tilde {B}\tilde {C}$ is a connecting domain for ![]() $\tilde {C}$. Hence,
$\tilde {C}$. Hence,
 \begin{align*} \delta(\gamma,\gamma')+\delta(\gamma',\gamma'') &= \big(\delta(y)-\delta(x)-2e(\varphi)+\tfrac{1}{2}\big)+ \big(\delta(z)-\delta(y)-2e(\varphi')+\tfrac{1}{2}\big) \\ &= \delta(z)-\delta(x)-2e(\varphi+\varphi'+\Delta\tilde{A}\tilde{B}\tilde{C})+\tfrac{1}{2} = \delta(\gamma,\gamma''). \end{align*}
\begin{align*} \delta(\gamma,\gamma')+\delta(\gamma',\gamma'') &= \big(\delta(y)-\delta(x)-2e(\varphi)+\tfrac{1}{2}\big)+ \big(\delta(z)-\delta(y)-2e(\varphi')+\tfrac{1}{2}\big) \\ &= \delta(z)-\delta(x)-2e(\varphi+\varphi'+\Delta\tilde{A}\tilde{B}\tilde{C})+\tfrac{1}{2} = \delta(\gamma,\gamma''). \end{align*}
Lemma 4.20 Given two curves with local systems ![]() $\gamma$ and
$\gamma$ and ![]() $\gamma '$ in
$\gamma '$ in ![]() $S^2_4$ that share the same slope
$S^2_4$ that share the same slope ![]() $s\in \operatorname {\mathbb {Q}P}^1$, the vector space
$s\in \operatorname {\mathbb {Q}P}^1$, the vector space ![]() $\operatorname {HF}(\gamma,\gamma ')$ is either zero or it is supported in two consecutive
$\operatorname {HF}(\gamma,\gamma ')$ is either zero or it is supported in two consecutive ![]() $\delta$-gradings, namely
$\delta$-gradings, namely ![]() $\delta (\gamma,\gamma ')$ and
$\delta (\gamma,\gamma ')$ and ![]() $\delta (\gamma,\gamma ')+1$. Moreover, if
$\delta (\gamma,\gamma ')+1$. Moreover, if ![]() $\gamma$ is rational and
$\gamma$ is rational and ![]() $\gamma '$ is special, or vice versa, then
$\gamma '$ is special, or vice versa, then ![]() $\operatorname {HF}(\gamma,\gamma ')=0$. Finally, for two rational curves with trivial local systems
$\operatorname {HF}(\gamma,\gamma ')=0$. Finally, for two rational curves with trivial local systems ![]() $\operatorname {HF}(\mathbf {r}(s),\mathbf {r}(s))\neq 0$, as well as for special curves
$\operatorname {HF}(\mathbf {r}(s),\mathbf {r}(s))\neq 0$, as well as for special curves ![]() $\operatorname {HF}(\mathbf {s}_n(s;{\mathsf {i}},{\mathsf {j}}),\mathbf {s}_m(s;{\mathsf {i}},{\mathsf {j}}))\neq 0$ (given any
$\operatorname {HF}(\mathbf {s}_n(s;{\mathsf {i}},{\mathsf {j}}),\mathbf {s}_m(s;{\mathsf {i}},{\mathsf {j}}))\neq 0$ (given any ![]() $n,m>0$ and pair
$n,m>0$ and pair ![]() $({\mathsf {i}},{\mathsf {j}})$ of tangle ends compatible with the slope
$({\mathsf {i}},{\mathsf {j}})$ of tangle ends compatible with the slope ![]() $s$).
$s$).
Proof. Let us consider each combination of rational and special curves separately. Clearly, the Lagrangian Floer homology of a special and a rational curve vanishes. To compute the Lagrangian Floer homology of two rational curves with local systems of the same slope, we can apply [Reference ZibrowiusZib20, Theorem 4.45] to verify the first statement in this case. If the two local systems are trivial, then their Lagrangian Floer homology does not vanish by [Reference ZibrowiusZib20, Lemma 4.51]. Now let us turn to the final case that ![]() $\gamma$ and
$\gamma$ and ![]() $\gamma '$ are special. Then, if they wrap around different tangle ends, their Lagrangian Floer homology vanishes. Thus, let us consider
$\gamma '$ are special. Then, if they wrap around different tangle ends, their Lagrangian Floer homology vanishes. Thus, let us consider ![]() $\gamma =\mathbf {s}_n(s;{\mathsf {i}},{\mathsf {j}})$ and
$\gamma =\mathbf {s}_n(s;{\mathsf {i}},{\mathsf {j}})$ and ![]() $\gamma '=\mathbf {s}_m(s;{\mathsf {i}},{\mathsf {j}})$. To justify the support of
$\gamma '=\mathbf {s}_m(s;{\mathsf {i}},{\mathsf {j}})$. To justify the support of ![]() $\operatorname {HF}(\gamma,\gamma ')$ for
$\operatorname {HF}(\gamma,\gamma ')$ for ![]() $n\neq m$, we can argue as follows. Let us consider a straight line of slope
$n\neq m$, we can argue as follows. Let us consider a straight line of slope ![]() $s$ through two integer lattice points
$s$ through two integer lattice points ![]() $\tilde {{\mathsf {i}}}$ and
$\tilde {{\mathsf {i}}}$ and ![]() $\tilde {{\mathsf {j}}}$ corresponding to the tangle ends
$\tilde {{\mathsf {j}}}$ corresponding to the tangle ends ![]() ${\mathsf {i}}$ and
${\mathsf {i}}$ and ![]() ${\mathsf {j}}$, respectively. After some homotopy, we may assume that
${\mathsf {j}}$, respectively. After some homotopy, we may assume that ![]() $\gamma$ and
$\gamma$ and ![]() $\gamma '$ are contained in a small neighborhood of the embedded arc that is the image of this straight line in
$\gamma '$ are contained in a small neighborhood of the embedded arc that is the image of this straight line in ![]() $S^2_4$. Moreover, we may assume that the slopes of any lifts of
$S^2_4$. Moreover, we may assume that the slopes of any lifts of ![]() $\gamma$ and
$\gamma$ and ![]() $\gamma '$ are contained in
$\gamma '$ are contained in ![]() $(s-\varepsilon,s+\varepsilon )$ for some small
$(s-\varepsilon,s+\varepsilon )$ for some small ![]() $\varepsilon >0$. Now given some intersection point
$\varepsilon >0$. Now given some intersection point ![]() $\bullet \in \operatorname {HF}(\gamma,\gamma ')$, choose lifts
$\bullet \in \operatorname {HF}(\gamma,\gamma ')$, choose lifts ![]() $\bar {\gamma }$ and
$\bar {\gamma }$ and ![]() $\bar {\gamma }'$ that intersect transversely in some lift
$\bar {\gamma }'$ that intersect transversely in some lift ![]() $\tilde {\bullet }$ of
$\tilde {\bullet }$ of ![]() $\bullet$. Let
$\bullet$. Let ![]() $t$ and
$t$ and ![]() $t'$ be the slopes of
$t'$ be the slopes of ![]() $\bar {\gamma }$ and
$\bar {\gamma }$ and ![]() $\bar {\gamma }'$ at
$\bar {\gamma }'$ at ![]() $\tilde {\bullet }$, respectively. Then
$\tilde {\bullet }$, respectively. Then
 \[ \delta(\bullet)= \begin{cases} \delta(\gamma,\gamma') & \text{if }s-\varepsilon< t'< t< s+\varepsilon,\\ \delta(\gamma,\gamma')+1 & \text{if } s-\varepsilon< t< t'< s+\varepsilon, \end{cases} \]
\[ \delta(\bullet)= \begin{cases} \delta(\gamma,\gamma') & \text{if }s-\varepsilon< t'< t< s+\varepsilon,\\ \delta(\gamma,\gamma')+1 & \text{if } s-\varepsilon< t< t'< s+\varepsilon, \end{cases} \]
which can be seen by applying Lemma 4.7 to thin triangular domains enclosed on two sides by ![]() $\bar {\gamma }$ and
$\bar {\gamma }$ and ![]() $\bar {\gamma }'$ and on the third side by either only the vertical or only the horizontal arcs in
$\bar {\gamma }'$ and on the third side by either only the vertical or only the horizontal arcs in ![]() $P$ (see also Figure 9(a)).
$P$ (see also Figure 9(a)).
There exist local systems ![]() $X$ and
$X$ and ![]() $Y$ for which
$Y$ for which ![]() $\operatorname {HF}(\mathbf {r}_X(s),\mathbf {r}_Y(s))=0$. For example, take
$\operatorname {HF}(\mathbf {r}_X(s),\mathbf {r}_Y(s))=0$. For example, take ![]() $X$ to be a permutation matrix of order
$X$ to be a permutation matrix of order ![]() $n$ and let
$n$ and let ![]() $Y$ be the companion matrix of the polynomial
$Y$ be the companion matrix of the polynomial ![]() $f(x)=x^n+x+1$. Then
$f(x)=x^n+x+1$. Then ![]() $\ker (f(X))=\ker (X)=0$, so by [Reference ZibrowiusZib20, Theorem 4.45 and Lemma 4.51],
$\ker (f(X))=\ker (X)=0$, so by [Reference ZibrowiusZib20, Theorem 4.45 and Lemma 4.51], ![]() $\dim \operatorname {HF}(\mathbf {r}_X(s),\mathbf {r}_Y(s))=2\cdot \dim \ker (f(X))=0$. However, we still have some control over local systems.
$\dim \operatorname {HF}(\mathbf {r}_X(s),\mathbf {r}_Y(s))=2\cdot \dim \ker (f(X))=0$. However, we still have some control over local systems.
Definition 4.21 We say two local systems ![]() $X$ and
$X$ and ![]() $Y$ are complementary, if
$Y$ are complementary, if ![]() $\operatorname {HF}(\mathbf {r}_X(s),\mathbf {r}_Y(s))$ vanishes, where
$\operatorname {HF}(\mathbf {r}_X(s),\mathbf {r}_Y(s))$ vanishes, where ![]() $s$ is some slope. We call a local system inhibited if it is complementary to the (trivial) one-dimensional local system. Similarly, we call a rational curve inhibited if its local system is inhibited. We call a collection of curves
$s$ is some slope. We call a local system inhibited if it is complementary to the (trivial) one-dimensional local system. Similarly, we call a rational curve inhibited if its local system is inhibited. We call a collection of curves ![]() $\Gamma$
$\Gamma$ ![]() $s$-inhibited if any rational component of slope
$s$-inhibited if any rational component of slope ![]() $s$ is inhibited.
$s$ is inhibited.
Lemma 4.22 If ![]() $X$ and
$X$ and ![]() $Y$ are complementary local systems, then at least one of
$Y$ are complementary local systems, then at least one of ![]() $X$ and
$X$ and ![]() $Y$ is inhibited.
$Y$ is inhibited.
Proof. We show the contrapositive: if ![]() $\operatorname {HF}(\mathbf {r}_X(s),\mathbf {r}(s))$ and
$\operatorname {HF}(\mathbf {r}_X(s),\mathbf {r}(s))$ and ![]() $\operatorname {HF}(\mathbf {r}_Y(s),\mathbf {r}(s))$ are non-zero, then so is
$\operatorname {HF}(\mathbf {r}_Y(s),\mathbf {r}(s))$ are non-zero, then so is ![]() $\operatorname {HF}(\mathbf {r}_X(s),\mathbf {r}_Y(s))$. Let us first verify this in the case that
$\operatorname {HF}(\mathbf {r}_X(s),\mathbf {r}_Y(s))$. Let us first verify this in the case that ![]() $X$ and
$X$ and ![]() $Y$ are companion matrices
$Y$ are companion matrices ![]() $X_f$ and
$X_f$ and ![]() $X_g$ of two polynomials
$X_g$ of two polynomials ![]() $f,g\in \mathbb {F}[x]$, respectively. By [Reference ZibrowiusZib20, Theorem 4.45 and Lemma 4.51],
$f,g\in \mathbb {F}[x]$, respectively. By [Reference ZibrowiusZib20, Theorem 4.45 and Lemma 4.51], ![]() $\operatorname {HF}(\mathbf {r}_{X_f}(s),\mathbf {r}_{X_g}(s))$ is zero if and only if the matrix
$\operatorname {HF}(\mathbf {r}_{X_f}(s),\mathbf {r}_{X_g}(s))$ is zero if and only if the matrix ![]() $f(X_g)$ is invertible. Similarly
$f(X_g)$ is invertible. Similarly ![]() $\operatorname {HF}(\mathbf {r}_{X_f}(s),\mathbf {r}(s))$ is zero if and only if
$\operatorname {HF}(\mathbf {r}_{X_f}(s),\mathbf {r}(s))$ is zero if and only if ![]() $f(1)$ is invertible, i.e. equal to
$f(1)$ is invertible, i.e. equal to ![]() $1$; the same is true of course for
$1$; the same is true of course for ![]() $g$. Thus, we need to show that
$g$. Thus, we need to show that ![]() $f(1)=0=g(1)$ implies that
$f(1)=0=g(1)$ implies that ![]() $f(X_g)$ is not invertible. This follows from two observations. First, note that
$f(X_g)$ is not invertible. This follows from two observations. First, note that ![]() $\det (X_g+1)=g(1)=0$, because
$\det (X_g+1)=g(1)=0$, because ![]() $g$ is the characteristic polynomial of
$g$ is the characteristic polynomial of ![]() $X_g$, so
$X_g$, so ![]() $(X_g+1)$ is not invertible. Second,
$(X_g+1)$ is not invertible. Second, ![]() $f(1)=0$ implies that there exists some polynomial
$f(1)=0$ implies that there exists some polynomial ![]() $\tilde {f}\in \mathbb {F}[x]$ such that
$\tilde {f}\in \mathbb {F}[x]$ such that ![]() $f(x)=(x+1)\tilde {f}(x)$. Thus, if
$f(x)=(x+1)\tilde {f}(x)$. Thus, if ![]() $(X_g+1)$ is not invertible, then neither is
$(X_g+1)$ is not invertible, then neither is ![]() $f(X_g)$.
$f(X_g)$.
In the general case, ![]() $\mathbf {r}_X$ and
$\mathbf {r}_X$ and ![]() $\mathbf {r}_Y$ are equivalent to disjoint unions of rational curves
$\mathbf {r}_Y$ are equivalent to disjoint unions of rational curves ![]() $\mathbf {r}_{X_i}$ and
$\mathbf {r}_{X_i}$ and ![]() $\mathbf {r}_{Y_j}$, respectively, whose local systems are all companion matrices. Suppose there exist
$\mathbf {r}_{Y_j}$, respectively, whose local systems are all companion matrices. Suppose there exist ![]() $i,j$ such that
$i,j$ such that ![]() $X_i$ and
$X_i$ and ![]() $Y_j$ are not inhibited. Then, by the above,
$Y_j$ are not inhibited. Then, by the above, ![]() $X_i$ and
$X_i$ and ![]() $Y_j$ are not complementary, so
$Y_j$ are not complementary, so ![]() $X$ and
$X$ and ![]() $Y$ are not complementary.
$Y$ are not complementary.
Remark 4.23 We would like to show that no rational component of ![]() $\operatorname {HFT}(T)$ is inhibited for any Conway tangle
$\operatorname {HFT}(T)$ is inhibited for any Conway tangle ![]() $T$. However, the only known restriction is that after combining the local systems of all parallel rational components, the new local system should be conjugate to its inverse [Reference ZibrowiusZib23b, Theorem 0.10]. There are many such local systems: for example, for any invertible matrix
$T$. However, the only known restriction is that after combining the local systems of all parallel rational components, the new local system should be conjugate to its inverse [Reference ZibrowiusZib23b, Theorem 0.10]. There are many such local systems: for example, for any invertible matrix ![]() $X$, the diagonal block matrix
$X$, the diagonal block matrix ![]() $Y$ with blocks
$Y$ with blocks ![]() $X$ and
$X$ and ![]() $X^{-1}$ is conjugate to its inverse. If we choose
$X^{-1}$ is conjugate to its inverse. If we choose ![]() $X$ to be inhibited, then so is
$X$ to be inhibited, then so is ![]() $Y$.
$Y$.
Definition 4.24 We say a multicurve ![]() $\Gamma$ is exceptional if
$\Gamma$ is exceptional if ![]() $\operatorname {\mathcal {S}}_{\Gamma }=\{s,s'\}$ for two distinct slopes
$\operatorname {\mathcal {S}}_{\Gamma }=\{s,s'\}$ for two distinct slopes ![]() $s,s'\in \operatorname {\mathbb {Q}P}^1$ and there exists a constant
$s,s'\in \operatorname {\mathbb {Q}P}^1$ and there exists a constant ![]() $c\neq 0,1$ such that
$c\neq 0,1$ such that ![]() $\delta (\gamma,\gamma ')=c$ for all components
$\delta (\gamma,\gamma ')=c$ for all components ![]() $\gamma,\gamma '\in \Gamma$ in slopes
$\gamma,\gamma '\in \Gamma$ in slopes ![]() $s,s'$, respectively. We say that a tangle
$s,s'$, respectively. We say that a tangle ![]() $T$ is Heegaard Floer exceptional if
$T$ is Heegaard Floer exceptional if ![]() $\operatorname {HFT}(T)$ is exceptional.
$\operatorname {HFT}(T)$ is exceptional.
A tangle that is Heegaard Floer exceptional is described in Example 7.15.
4.3 Heegaard Floer thin fillings
In this subsection, ![]() $G$ is either
$G$ is either ![]() $\mathbb {Z}$ or
$\mathbb {Z}$ or ![]() $\mathbb {Z}/2$. Define
$\mathbb {Z}/2$. Define
In the following, we make implicit use of the following properties that the curves in ![]() $\operatorname {\mathfrak {C}_{\operatorname {HF}}}$ are known to satisfy: each multicurve
$\operatorname {\mathfrak {C}_{\operatorname {HF}}}$ are known to satisfy: each multicurve ![]() $\Gamma \in \operatorname {\mathfrak {C}_{\operatorname {HF}}}$ consists of linear components only (Theorem 3.9). Moreover, special components come in conjugate pairs of curves that are supported in identical
$\Gamma \in \operatorname {\mathfrak {C}_{\operatorname {HF}}}$ consists of linear components only (Theorem 3.9). Moreover, special components come in conjugate pairs of curves that are supported in identical ![]() $\delta$-gradings (Theorem 3.10). Finally,
$\delta$-gradings (Theorem 3.10). Finally, ![]() $\operatorname {HF}(\Gamma _1,\Gamma _2)\neq 0$ for each
$\operatorname {HF}(\Gamma _1,\Gamma _2)\neq 0$ for each ![]() $\Gamma _1,\Gamma _2\in \operatorname {\mathfrak {C}_{\operatorname {HF}}}$, because of Theorem 3.5 and the fact that knot Floer homology does not vanish. In particular, if
$\Gamma _1,\Gamma _2\in \operatorname {\mathfrak {C}_{\operatorname {HF}}}$, because of Theorem 3.5 and the fact that knot Floer homology does not vanish. In particular, if ![]() $\operatorname {\mathcal {S}}_\Gamma =\{s\}$ for some
$\operatorname {\mathcal {S}}_\Gamma =\{s\}$ for some ![]() $\Gamma \in \operatorname {\mathfrak {C}_{\operatorname {HF}}}$, then
$\Gamma \in \operatorname {\mathfrak {C}_{\operatorname {HF}}}$, then ![]() $\Gamma$ contains some rational component whose local system is not inhibited. Let
$\Gamma$ contains some rational component whose local system is not inhibited. Let ![]() $\operatorname {\mathfrak {C}^\mathrm {wb}_{\operatorname {HF}}}\subseteq \operatorname {\mathfrak {C}_{\operatorname {HF}}}$ be the subset of well-behaved multicurves defined by
$\operatorname {\mathfrak {C}^\mathrm {wb}_{\operatorname {HF}}}\subseteq \operatorname {\mathfrak {C}_{\operatorname {HF}}}$ be the subset of well-behaved multicurves defined by
Given two multicurves ![]() $\Gamma$ and
$\Gamma$ and ![]() $\Gamma '$ and a slope
$\Gamma '$ and a slope ![]() $s\in \operatorname {\mathcal {S}}_\Gamma \cap \operatorname {\mathcal {S}}_{\Gamma '}$, the following two local conditions will be relevant.
$s\in \operatorname {\mathcal {S}}_\Gamma \cap \operatorname {\mathcal {S}}_{\Gamma '}$, the following two local conditions will be relevant.
Condition (R) At least one of
 $\Gamma$ and
$\Gamma$ and  $\Gamma '$ is
$\Gamma '$ is  $s$-rational, i.e. it only contains rational components of slope
$s$-rational, i.e. it only contains rational components of slope  $s$.
$s$.Condition (R ⋆) The local systems of any two rational components of
 $\Gamma$ and
$\Gamma$ and  $\Gamma '$ of slope
$\Gamma '$ of slope  $s$ are complementary.
$s$ are complementary.
These are the local conditions for Heegaard Floer theory mentioned in Theorems 1.12 and 1.15. Note that (R![]() $_\star$) is vacuously satisfied if any two rational components of
$_\star$) is vacuously satisfied if any two rational components of ![]() $\Gamma$ and
$\Gamma$ and ![]() $\Gamma '$ have different slopes. For instance, this is true if
$\Gamma '$ have different slopes. For instance, this is true if ![]() $\Gamma =\operatorname {m}(\operatorname {HFT}(T_1))$,
$\Gamma =\operatorname {m}(\operatorname {HFT}(T_1))$, ![]() $\Gamma '=\operatorname {HFT}(T_2)$, and
$\Gamma '=\operatorname {HFT}(T_2)$, and ![]() $T_1\cup T_2$ is a knot, see Lemma 3.11.
$T_1\cup T_2$ is a knot, see Lemma 3.11.
Definition 4.25 A ![]() $\delta$-graded vector space is
$\delta$-graded vector space is ![]() $\boldsymbol {\mathbb {Z}}$-thin if it is thin and
$\boldsymbol {\mathbb {Z}}$-thin if it is thin and ![]() $\boldsymbol {\mathbb {Z}/2}$-thin if it is supported in at most one
$\boldsymbol {\mathbb {Z}/2}$-thin if it is supported in at most one ![]() $\delta$-grading modulo 2. In particular, the 0-dimensional vector space is
$\delta$-grading modulo 2. In particular, the 0-dimensional vector space is ![]() $G$-thin for both
$G$-thin for both ![]() $G=\mathbb {Z}$ and
$G=\mathbb {Z}$ and ![]() $G=\mathbb {Z}/2$. Given a relatively
$G=\mathbb {Z}/2$. Given a relatively ![]() $\delta$-graded multicurve
$\delta$-graded multicurve ![]() $\Gamma$, define the space of
$\Gamma$, define the space of ![]() $\boldsymbol {G}$-thin rational fillings of
$\boldsymbol {G}$-thin rational fillings of ![]() $\Gamma$ by
$\Gamma$ by
Suppose ![]() $T$ is a Conway tangle in a three-ball. Then, by Theorem 3.5, writing
$T$ is a Conway tangle in a three-ball. Then, by Theorem 3.5, writing
recovers the definitions of ![]() $\Theta _{\mathrm {HF}}(T)$ and
$\Theta _{\mathrm {HF}}(T)$ and ![]() $\mathrm {A}_{\mathrm {HF}}(T)$ from the introduction.
$\mathrm {A}_{\mathrm {HF}}(T)$ from the introduction.
Remark 4.26 Since by Lemma 3.7 the tangle invariant ![]() $\operatorname {HFT}$ behaves in a natural way under mirroring,
$\operatorname {HFT}$ behaves in a natural way under mirroring, ![]() $\Theta _{\mathrm {HF}}(T^*)=\Theta ^{\operatorname {m}}_{\mathrm {HF}}(T)$ and
$\Theta _{\mathrm {HF}}(T^*)=\Theta ^{\operatorname {m}}_{\mathrm {HF}}(T)$ and ![]() $\mathrm {A}_{\mathrm {HF}}(T^*)=\mathrm {A}_{\mathrm {HF}}^{\operatorname {m}}(T)$ for any Conway tangle
$\mathrm {A}_{\mathrm {HF}}(T^*)=\mathrm {A}_{\mathrm {HF}}^{\operatorname {m}}(T)$ for any Conway tangle ![]() $T$.
$T$.
The following is the main technical result which links § 2 to the present discussion about ![]() $\operatorname {HFT}$, by relating elements of
$\operatorname {HFT}$, by relating elements of ![]() $\operatorname {\mathfrak {C}_{\operatorname {HF}}}$ to line sets in § 2. Recall that a line set is simply a finite collection of elements of
$\operatorname {\mathfrak {C}_{\operatorname {HF}}}$ to line sets in § 2. Recall that a line set is simply a finite collection of elements of ![]() $\operatorname {\mathfrak {C}}=\operatorname {\mathbb {Q}P}^1\times \,G\times \{0,1\}$. We write
$\operatorname {\mathfrak {C}}=\operatorname {\mathbb {Q}P}^1\times \,G\times \{0,1\}$. We write ![]() $\mathcal {P}_{\mathrm {finite}}(\operatorname {\mathfrak {C}})$ for the set of all line sets.
$\mathcal {P}_{\mathrm {finite}}(\operatorname {\mathfrak {C}})$ for the set of all line sets.
Theorem 4.27 There exist maps ![]() $\operatorname {g}\colon \thinspace \operatorname {\mathfrak {C}}^2\rightarrow G$ and
$\operatorname {g}\colon \thinspace \operatorname {\mathfrak {C}}^2\rightarrow G$ and ![]() $\Phi \colon \thinspace \operatorname {\mathfrak {C}_{\operatorname {HF}}}\rightarrow \mathcal {P}_\mathrm {finite}(\operatorname {\mathfrak {C}})$, where
$\Phi \colon \thinspace \operatorname {\mathfrak {C}_{\operatorname {HF}}}\rightarrow \mathcal {P}_\mathrm {finite}(\operatorname {\mathfrak {C}})$, where ![]() $\operatorname {g}$ satisfies (symmetry), (transitivity), and (linearity) as in § 2, and such that for any
$\operatorname {g}$ satisfies (symmetry), (transitivity), and (linearity) as in § 2, and such that for any ![]() $\Gamma \in \operatorname {\mathfrak {C}_{\operatorname {HF}}}$ the following hold:
$\Gamma \in \operatorname {\mathfrak {C}_{\operatorname {HF}}}$ the following hold:
(i)
 $\operatorname {\mathcal {S}}_{\Gamma }=\operatorname {\mathcal {S}}_{\Phi (\Gamma )}$;
$\operatorname {\mathcal {S}}_{\Gamma }=\operatorname {\mathcal {S}}_{\Phi (\Gamma )}$;(ii)
 $\Theta _{\mathit {G}}(\Gamma )=\Theta _{\mathit {G}}(\Phi (\Gamma ))$;
$\Theta _{\mathit {G}}(\Gamma )=\Theta _{\mathit {G}}(\Phi (\Gamma ))$;(iii)
 $\Phi (\Gamma )$ is non-trivial;
$\Phi (\Gamma )$ is non-trivial;(iv)
 $\Phi (\Gamma )$ is exceptional if and only if
$\Phi (\Gamma )$ is exceptional if and only if  $\Gamma$ is exceptional.
$\Gamma$ is exceptional.
Moreover, if ![]() $\Gamma,\Gamma '\in \operatorname {\mathfrak {C}^\mathrm {wb}_{\operatorname {HF}}}$:
$\Gamma,\Gamma '\in \operatorname {\mathfrak {C}^\mathrm {wb}_{\operatorname {HF}}}$:
(v) for any slope
 $s\in \operatorname {\mathbb {Q}P}^1$,
$s\in \operatorname {\mathbb {Q}P}^1$,  $\Gamma$ is
$\Gamma$ is  $s$-rational if and only if
$s$-rational if and only if  $\Phi (\Gamma )$ is
$\Phi (\Gamma )$ is  $s$-rational;
$s$-rational;(vi)
 $\operatorname {HF}(\Gamma,\Gamma ')$ is
$\operatorname {HF}(\Gamma,\Gamma ')$ is  $G$-thin if and only if the pair
$G$-thin if and only if the pair  $(\Phi (\Gamma ), \Phi (\Gamma '))$ is
$(\Phi (\Gamma ), \Phi (\Gamma '))$ is  $G$-thin.
$G$-thin.
Proof. Given ![]() $c\in \operatorname {\mathfrak {C}}$, let
$c\in \operatorname {\mathfrak {C}}$, let ![]() $\gamma (c)$ be an absolutely
$\gamma (c)$ be an absolutely ![]() $\delta$-graded linear curve of slope
$\delta$-graded linear curve of slope ![]() $s(c)$ such that
$s(c)$ such that ![]() $\delta _{-}(\gamma (c))=\operatorname {g}(c)$ if
$\delta _{-}(\gamma (c))=\operatorname {g}(c)$ if ![]() $s(c)\neq 0$ and
$s(c)\neq 0$ and ![]() $\delta _{|}(\gamma (c))=\operatorname {g}(c)-\tfrac {1}{2}$ if
$\delta _{|}(\gamma (c))=\operatorname {g}(c)-\tfrac {1}{2}$ if ![]() $s(c)=0$. (Whether this curve is rational or special has no bearing on what follows.) Now define
$s(c)=0$. (Whether this curve is rational or special has no bearing on what follows.) Now define ![]() $\operatorname {g}\colon \thinspace \operatorname {\mathfrak {C}}^2\rightarrow G$ by setting for each
$\operatorname {g}\colon \thinspace \operatorname {\mathfrak {C}}^2\rightarrow G$ by setting for each ![]() $c,c' \in \operatorname {\mathfrak {C}}$
$c,c' \in \operatorname {\mathfrak {C}}$
(Note that the order of ![]() $c$ and
$c$ and ![]() $c'$ is reversed.) Then, by Corollary 4.18, (symmetry) of
$c'$ is reversed.) Then, by Corollary 4.18, (symmetry) of ![]() $\operatorname {g}$ holds, and by Theorem 4.19, so does (transitivity) of
$\operatorname {g}$ holds, and by Theorem 4.19, so does (transitivity) of ![]() $\operatorname {g}$. Moreover, (linearity) of
$\operatorname {g}$. Moreover, (linearity) of ![]() $\operatorname {g}$ follows from the definition.
$\operatorname {g}$ follows from the definition.
Before we define the map ![]() $\Phi$, let us lift the
$\Phi$, let us lift the ![]() $\delta$-grading of each multicurve
$\delta$-grading of each multicurve ![]() $\Gamma =\operatorname {HFT}(T)\in \operatorname {\mathfrak {C}_{\operatorname {HF}}}$ to an absolute
$\Gamma =\operatorname {HFT}(T)\in \operatorname {\mathfrak {C}_{\operatorname {HF}}}$ to an absolute ![]() $\delta$-grading such that
$\delta$-grading such that ![]() $\delta _{-}(\gamma )\in \mathbb {Z}$ and
$\delta _{-}(\gamma )\in \mathbb {Z}$ and ![]() $\delta _{|}(\gamma )\in \mathbb {Z}+\tfrac 1 2$ for each component
$\delta _{|}(\gamma )\in \mathbb {Z}+\tfrac 1 2$ for each component ![]() $\gamma$ of
$\gamma$ of ![]() $\Gamma$. For rational tangles
$\Gamma$. For rational tangles ![]() $T=Q_s$, this is clearly possible. To see that this is possible for arbitrary Conway tangles
$T=Q_s$, this is clearly possible. To see that this is possible for arbitrary Conway tangles ![]() $T$, we choose a slope
$T$, we choose a slope ![]() $s\not \in \operatorname {\mathcal {S}}_{\Gamma }$. Then
$s\not \in \operatorname {\mathcal {S}}_{\Gamma }$. Then ![]() $\operatorname {HF}(\mathbf {r}(s),\Gamma )$ computes the (potentially once stabilized) knot Floer homology of
$\operatorname {HF}(\mathbf {r}(s),\Gamma )$ computes the (potentially once stabilized) knot Floer homology of ![]() $Q_{-s}\cup T$, which, up to an overall grading shift, is supported in integer
$Q_{-s}\cup T$, which, up to an overall grading shift, is supported in integer ![]() $\delta$-gradings. By our choice of slope
$\delta$-gradings. By our choice of slope ![]() $s$,
$s$, ![]() $\mathbf {r}(s)$ intersects each component of
$\mathbf {r}(s)$ intersects each component of ![]() $\Gamma$ non-trivially, so using Lemma 4.17, we can get an absolute lift with the desired properties. Which lift we pick is ultimately irrelevant, but it will change the definition of the map
$\Gamma$ non-trivially, so using Lemma 4.17, we can get an absolute lift with the desired properties. Which lift we pick is ultimately irrelevant, but it will change the definition of the map ![]() $\Phi$.
$\Phi$.
Now, we are ready to define the map ![]() $\Phi$. Given some absolutely
$\Phi$. Given some absolutely ![]() $\delta$-graded rational or special curve
$\delta$-graded rational or special curve ![]() $\gamma$ of slope
$\gamma$ of slope ![]() $s$, let
$s$, let ![]() $c=c(\gamma )\in \operatorname {\mathfrak {C}}$ be the line defined by
$c=c(\gamma )\in \operatorname {\mathfrak {C}}$ be the line defined by ![]() $s(c)=s$,
$s(c)=s$, ![]() $\operatorname {g}(c)=\delta _{-}(\gamma )$ if
$\operatorname {g}(c)=\delta _{-}(\gamma )$ if ![]() $s\neq 0$ and
$s\neq 0$ and ![]() $\delta _{|}(\gamma )+\tfrac {1}{2}$ if
$\delta _{|}(\gamma )+\tfrac {1}{2}$ if ![]() $s(c)=0$, and
$s(c)=0$, and ![]() $\varepsilon (c)=1$ if
$\varepsilon (c)=1$ if ![]() $\gamma$ is special or rational with inhibited local system and
$\gamma$ is special or rational with inhibited local system and ![]() $\varepsilon (c)=0$ otherwise. Then, given some
$\varepsilon (c)=0$ otherwise. Then, given some ![]() $\Gamma =\{\gamma _i\}_i\in \operatorname {\mathfrak {C}_{\operatorname {HF}}}$, define
$\Gamma =\{\gamma _i\}_i\in \operatorname {\mathfrak {C}_{\operatorname {HF}}}$, define ![]() $\Phi (\Gamma )$ as the set corresponding to the multiset
$\Phi (\Gamma )$ as the set corresponding to the multiset ![]() $\{c(\gamma _i)\}_{i}$.
$\{c(\gamma _i)\}_{i}$.
Clearly, properties (i)–(iv) hold by construction. Moreover, the only rational components that ![]() $\Phi$ sends to special lines are those with inhibited local systems, so property (v) follows. Suppose
$\Phi$ sends to special lines are those with inhibited local systems, so property (v) follows. Suppose ![]() $\Gamma,\Gamma '\in \operatorname {\mathfrak {C}^\mathrm {wb}_{\operatorname {HF}}}$. Then by Lemma 4.22, these multicurves do not contain any rational components that are complementary to each other. Thus, if
$\Gamma,\Gamma '\in \operatorname {\mathfrak {C}^\mathrm {wb}_{\operatorname {HF}}}$. Then by Lemma 4.22, these multicurves do not contain any rational components that are complementary to each other. Thus, if ![]() $\gamma \in \Gamma$ and
$\gamma \in \Gamma$ and ![]() $\gamma '\in \Gamma '$ are two components of the same slope,
$\gamma '\in \Gamma '$ are two components of the same slope, ![]() $\operatorname {HF}(\gamma,\gamma ')$ is
$\operatorname {HF}(\gamma,\gamma ')$ is ![]() $G$-thin if and only if
$G$-thin if and only if ![]() $(c(\gamma ),c(\gamma '))$ is
$(c(\gamma ),c(\gamma '))$ is ![]() $G$-thin by Lemma 4.20. Together with Lemma 4.17, this proves property (vi).
$G$-thin by Lemma 4.20. Together with Lemma 4.17, this proves property (vi).
We now establish the results concerning Heegaard Floer theory from the introduction. We restate these here for clarity. If we ignore the technical issue of inhibited curves and restrict to well-behaved multicurves, Theorems 1.12 and 1.15, specialized to the Heegaard Floer setting, follow immediately from the results of § 2 and Theorem 4.27. The proof in the general case requires a more careful analysis of the arguments from § 2.
Theorem 4.28 (Characterization of Heegaard Floer  $G$-thin filling spaces; Theorems 1.8 and 1.9)
$G$-thin filling spaces; Theorems 1.8 and 1.9)
For any Conway tangle ![]() $T$,
$T$, ![]() $\mathrm {A}_{\mathrm {HF}}(T)$ is either empty, a single point or an interval in
$\mathrm {A}_{\mathrm {HF}}(T)$ is either empty, a single point or an interval in ![]() $\operatorname {\mathbb {Q}P}^1$. Furthermore,
$\operatorname {\mathbb {Q}P}^1$. Furthermore, ![]() $\Theta _{\mathrm {HF}}(T)$ is either empty, a single point, two distinct points or an interval in
$\Theta _{\mathrm {HF}}(T)$ is either empty, a single point, two distinct points or an interval in ![]() $\operatorname {\mathbb {Q}P}^1$.
$\operatorname {\mathbb {Q}P}^1$.
Proposition 4.29 (Proposition 1.10)
If ![]() $\Theta _{\mathrm {HF}}(T)$ is an interval,
$\Theta _{\mathrm {HF}}(T)$ is an interval, ![]() $\Theta _{\mathrm {HF}}(T)=\mathrm {A}_{\mathrm {HF}}(T)$.
$\Theta _{\mathrm {HF}}(T)=\mathrm {A}_{\mathrm {HF}}(T)$.
In the following, let ![]() $T_1$ and
$T_1$ and ![]() $T_2$ be two Conway tangles and write
$T_2$ be two Conway tangles and write ![]() $\Gamma _1:= \operatorname {m}(\operatorname {HFT}(T_1))$ as well as
$\Gamma _1:= \operatorname {m}(\operatorname {HFT}(T_1))$ as well as ![]() $\Gamma _2:= \operatorname {HFT}(T_2)$.
$\Gamma _2:= \operatorname {HFT}(T_2)$.
Theorem 4.30 (A-link gluing theorem; Theorem 1.12)
The link ![]() $T_1\cup T_2$ is a Heegaard Floer A-link if and only if:
$T_1\cup T_2$ is a Heegaard Floer A-link if and only if:
(1)
 $\mathrm {A}_{\mathrm {HF}}^{\operatorname {m}}(T_1) \cup \mathrm {A}_{\mathrm {HF}}(T_2) = \operatorname {\mathbb {Q}P}^1$; and
$\mathrm {A}_{\mathrm {HF}}^{\operatorname {m}}(T_1) \cup \mathrm {A}_{\mathrm {HF}}(T_2) = \operatorname {\mathbb {Q}P}^1$; and(2) for every slope
 $s\in \partial \mathrm {A}_{\mathrm {HF}}^{\operatorname {m}}(T_1) \cap \partial \mathrm {A}_{\mathrm {HF}}(T_2)$,
$s\in \partial \mathrm {A}_{\mathrm {HF}}^{\operatorname {m}}(T_1) \cap \partial \mathrm {A}_{\mathrm {HF}}(T_2)$,  $\Gamma _1$ and
$\Gamma _1$ and  $\Gamma _2$ satisfy (R) and (R
$\Gamma _2$ satisfy (R) and (R $_\star$).
$_\star$).
Theorem 4.31 (Thin gluing theorem; Theorem 1.15)
Suppose at least one of ![]() $T_1$ and
$T_1$ and ![]() $T_2$ is not Heegaard Floer exceptional. Then
$T_2$ is not Heegaard Floer exceptional. Then ![]() $T_1\cup T_2$ is Heegaard Floer thin if and only if:
$T_1\cup T_2$ is Heegaard Floer thin if and only if:
(1)
 $\Theta ^{\operatorname {m}}_{\mathrm {HF}}(T_1) \cup \Theta _{\mathrm {HF}}(T_2) = \operatorname {\mathbb {Q}P}^1$; and
$\Theta ^{\operatorname {m}}_{\mathrm {HF}}(T_1) \cup \Theta _{\mathrm {HF}}(T_2) = \operatorname {\mathbb {Q}P}^1$; and(2) for every slope
 $s\in \partial \Theta _{\mathrm {HF}}^{\operatorname {m}}(T_1) \cap \partial \Theta _{\mathrm {HF}}(T_2)$,
$s\in \partial \Theta _{\mathrm {HF}}^{\operatorname {m}}(T_1) \cap \partial \Theta _{\mathrm {HF}}(T_2)$,  $\Gamma _1$ and
$\Gamma _1$ and  $\Gamma _2$ satisfy (R) and (R
$\Gamma _2$ satisfy (R) and (R $_\star$).
$_\star$).
The assumption in Theorem 4.31 that ![]() $T_1$ and
$T_1$ and ![]() $T_2$ not be both exceptional is meaningful; see Example 7.15.
$T_2$ not be both exceptional is meaningful; see Example 7.15.
Remark 4.32 The property (R![]() $_\star$) can be dropped from Theorems 4.30 and 4.31 if we restrict to well-behaved curves. Indeed, if
$_\star$) can be dropped from Theorems 4.30 and 4.31 if we restrict to well-behaved curves. Indeed, if ![]() $T_1\cup T_2$ is Heegaard Floer
$T_1\cup T_2$ is Heegaard Floer ![]() $G$-thin, then, clearly,
$G$-thin, then, clearly, ![]() $\Gamma _1$ and
$\Gamma _1$ and ![]() $\Gamma _2$ satisfy (R
$\Gamma _2$ satisfy (R![]() $_\star$) for any slope
$_\star$) for any slope ![]() $s\in \operatorname {\mathbb {Q}P}^1$. Conversely, suppose
$s\in \operatorname {\mathbb {Q}P}^1$. Conversely, suppose ![]() $\Gamma _1$ and
$\Gamma _1$ and ![]() $\Gamma _2$ are well-behaved. If
$\Gamma _2$ are well-behaved. If ![]() $\Theta _{\mathit {G}}(\Gamma _1) \cup \Theta _{\mathit {G}}(\Gamma _2) = \operatorname {\mathbb {Q}P}^1$, then for any slope
$\Theta _{\mathit {G}}(\Gamma _1) \cup \Theta _{\mathit {G}}(\Gamma _2) = \operatorname {\mathbb {Q}P}^1$, then for any slope ![]() $s\in \operatorname {\mathbb {Q}P}^1$, at least one of
$s\in \operatorname {\mathbb {Q}P}^1$, at least one of ![]() $\Gamma _1$ and
$\Gamma _1$ and ![]() $\Gamma _2$ does not contain any rational component of slope
$\Gamma _2$ does not contain any rational component of slope ![]() $s$, so
$s$, so ![]() $\Gamma _1$ and
$\Gamma _1$ and ![]() $\Gamma _2$ vacuously satisfy (R
$\Gamma _2$ vacuously satisfy (R![]() $_\star$) for all
$_\star$) for all ![]() $s\in \operatorname {\mathbb {Q}P}^1$.
$s\in \operatorname {\mathbb {Q}P}^1$.
Proofs of Theorems 4.30 and 4.31 for well-behaved multicurves Suppose ![]() $\Gamma _1,\Gamma _2\in \operatorname {\mathfrak {C}^\mathrm {wb}_{\operatorname {HF}}}$. Let
$\Gamma _1,\Gamma _2\in \operatorname {\mathfrak {C}^\mathrm {wb}_{\operatorname {HF}}}$. Let ![]() $C_i=\Phi (\Gamma _i)$ for
$C_i=\Phi (\Gamma _i)$ for ![]() $i=1,2$. By the previous remark, we may ignore property (R
$i=1,2$. By the previous remark, we may ignore property (R![]() $_\star$) for this proof. By Theorem 3.5,
$_\star$) for this proof. By Theorem 3.5, ![]() $T_1\cup T_2$ is an A-link if and only if
$T_1\cup T_2$ is an A-link if and only if ![]() $\operatorname {HF}(\Gamma _1,\Gamma _2)$ is
$\operatorname {HF}(\Gamma _1,\Gamma _2)$ is ![]() $\mathbb {Z}/2$-thin. By Theorem 4.27(vi), the latter is equivalent to
$\mathbb {Z}/2$-thin. By Theorem 4.27(vi), the latter is equivalent to ![]() $(C_1,C_2)$ being
$(C_1,C_2)$ being ![]() $\mathbb {Z}/2$-thin. Note that since
$\mathbb {Z}/2$-thin. Note that since ![]() $G=\mathbb {Z}/2$, neither
$G=\mathbb {Z}/2$, neither ![]() $C_1$ nor
$C_1$ nor ![]() $C_2$ are exceptional. Therefore, by Theorems 2.14 and 4.27(ii), (iii), and (v), this is equivalent to
$C_2$ are exceptional. Therefore, by Theorems 2.14 and 4.27(ii), (iii), and (v), this is equivalent to ![]() $\Theta _{\mathbb {Z}/2}(\Gamma _1)\cup \Theta _{\mathbb {Z}/2}(\Gamma _2)=\operatorname {\mathbb {Q}P}^1$ and for all
$\Theta _{\mathbb {Z}/2}(\Gamma _1)\cup \Theta _{\mathbb {Z}/2}(\Gamma _2)=\operatorname {\mathbb {Q}P}^1$ and for all ![]() $s\in \partial \Theta _{\mathbb {Z}/2}(\Gamma _1)\cap \partial \Theta _{\mathbb {Z}/2}(\Gamma _2)$, at least one of
$s\in \partial \Theta _{\mathbb {Z}/2}(\Gamma _1)\cap \partial \Theta _{\mathbb {Z}/2}(\Gamma _2)$, at least one of ![]() $\Gamma _1$ and
$\Gamma _1$ and ![]() $\Gamma _2$ is
$\Gamma _2$ is ![]() $s$-rational. This is equivalent to the right-hand side of Theorem 4.30.
$s$-rational. This is equivalent to the right-hand side of Theorem 4.30.
The proof of Theorem 4.31 is analogous to the above, noting that at most one of ![]() $C_1$ and
$C_1$ and ![]() $C_2$ are exceptional by Theorem 4.27(iv) and the additional hypothesis in Theorem 4.31.
$C_2$ are exceptional by Theorem 4.27(iv) and the additional hypothesis in Theorem 4.31.
Corollary 4.33 (Corollaries 1.13 and 1.16)
For any Conway tangles ![]() $T_1$ and
$T_1$ and ![]() $T_2$,
$T_2$,
 \begin{align*} \mathring{\mathrm{A}}_{\mathrm{HF}}^{\operatorname{m}}(T_1) \cup \mathring{\mathrm{A}}_{\mathrm{HF}}(T_2) &= \operatorname{\mathbb{Q}P}^1 \Rightarrow L \text{ is a Heegaard Floer A-link; and}\\ \mathring{\Theta}_{\mathrm{HF}}^{\operatorname{m}}(T_1) \cup \mathring{\Theta}_{\mathrm{HF}}(T_2) &= \operatorname{\mathbb{Q}P}^1 \Rightarrow L \text{ is Heegaard Floer thin}. \end{align*}
\begin{align*} \mathring{\mathrm{A}}_{\mathrm{HF}}^{\operatorname{m}}(T_1) \cup \mathring{\mathrm{A}}_{\mathrm{HF}}(T_2) &= \operatorname{\mathbb{Q}P}^1 \Rightarrow L \text{ is a Heegaard Floer A-link; and}\\ \mathring{\Theta}_{\mathrm{HF}}^{\operatorname{m}}(T_1) \cup \mathring{\Theta}_{\mathrm{HF}}(T_2) &= \operatorname{\mathbb{Q}P}^1 \Rightarrow L \text{ is Heegaard Floer thin}. \end{align*}
Proof of Corollary 4.33 for well-behaved multicurves Suppose that ![]() $\Gamma _1,\Gamma _2\in \operatorname {\mathfrak {C}^\mathrm {wb}_{\operatorname {HF}}}$. Let
$\Gamma _1,\Gamma _2\in \operatorname {\mathfrak {C}^\mathrm {wb}_{\operatorname {HF}}}$. Let ![]() $C_i=\Phi (\Gamma _i)$ for
$C_i=\Phi (\Gamma _i)$ for ![]() $i=1,2$ as before. By Theorem 4.27(iii),
$i=1,2$ as before. By Theorem 4.27(iii), ![]() $C_1$ and
$C_1$ and ![]() $C_2$ are non-trivial. By Theorem 4.27(ii), the hypotheses imply that
$C_2$ are non-trivial. By Theorem 4.27(ii), the hypotheses imply that ![]() $\mathring {\Theta }_{\mathit {G}}(C_1) \cup \mathring {\Theta }_{\mathit {G}}(C_2) = \operatorname {\mathbb {Q}P}^1$, and so by Corollary 2.16, the pair
$\mathring {\Theta }_{\mathit {G}}(C_1) \cup \mathring {\Theta }_{\mathit {G}}(C_2) = \operatorname {\mathbb {Q}P}^1$, and so by Corollary 2.16, the pair ![]() $(C_1,C_2)$ is
$(C_1,C_2)$ is ![]() $G$-thin. Thus, by Theorem 4.27(vi),
$G$-thin. Thus, by Theorem 4.27(vi), ![]() $\operatorname {HF}(\Gamma _1,\Gamma _2)$ is
$\operatorname {HF}(\Gamma _1,\Gamma _2)$ is ![]() $G$-thin. Now conclude with Theorem 3.5.
$G$-thin. Now conclude with Theorem 3.5.
Before proving Theorems 4.30 and 4.31 and Corollary 4.33 in general, let us translate Lemma 2.15 into the present setting.
Lemma 4.34 For any ![]() $\Gamma,\Gamma '\in \operatorname {\mathfrak {C}_{\operatorname {HF}}}$,
$\Gamma,\Gamma '\in \operatorname {\mathfrak {C}_{\operatorname {HF}}}$, ![]() $\Theta _{\mathit {G}}(\Gamma ) \cup \Theta _{\mathit {G}}(\Gamma ') =\operatorname {\mathbb {Q}P}^1$ implies
$\Theta _{\mathit {G}}(\Gamma ) \cup \Theta _{\mathit {G}}(\Gamma ') =\operatorname {\mathbb {Q}P}^1$ implies ![]() $\partial \Theta (\Gamma )\cap \partial \Theta (\Gamma ') = \operatorname {\mathcal {S}}_\Gamma \cap \operatorname {\mathcal {S}}_{\Gamma '}$.
$\partial \Theta (\Gamma )\cap \partial \Theta (\Gamma ') = \operatorname {\mathcal {S}}_\Gamma \cap \operatorname {\mathcal {S}}_{\Gamma '}$.
Proof. Let ![]() $C=\Phi (\Gamma )$ and
$C=\Phi (\Gamma )$ and ![]() $C'=\Phi (\Gamma ')$. By Theorem 4.27(iii),
$C'=\Phi (\Gamma ')$. By Theorem 4.27(iii), ![]() $C$ and
$C$ and ![]() $C'$ are non-trivial. By Theorem 4.27(ii),
$C'$ are non-trivial. By Theorem 4.27(ii), ![]() $\Theta (C)\cup \Theta (C')=\operatorname {\mathbb {Q}P}^1$ and
$\Theta (C)\cup \Theta (C')=\operatorname {\mathbb {Q}P}^1$ and ![]() $\partial \Theta _{\mathit {G}}(\Gamma ) \cap \partial \Theta _{\mathit {G}}(\Gamma ') = \partial \Theta (C) \cap \partial \Theta (C')$. By Lemma 2.15, the latter is equal to
$\partial \Theta _{\mathit {G}}(\Gamma ) \cap \partial \Theta _{\mathit {G}}(\Gamma ') = \partial \Theta (C) \cap \partial \Theta (C')$. By Lemma 2.15, the latter is equal to ![]() $\operatorname {\mathcal {S}}_{C}\cap \operatorname {\mathcal {S}}_{C'}$ which by Theorem 4.27(i) equals
$\operatorname {\mathcal {S}}_{C}\cap \operatorname {\mathcal {S}}_{C'}$ which by Theorem 4.27(i) equals ![]() $\operatorname {\mathcal {S}}_{\Gamma }\cap \operatorname {\mathcal {S}}_{\Gamma '}$.
$\operatorname {\mathcal {S}}_{\Gamma }\cap \operatorname {\mathcal {S}}_{\Gamma '}$.
Proof of Theorems 4.30 and 4.31 for general multicurves in ![]() By Lemma 4.34,
By Lemma 4.34, ![]() $\partial \Theta _{\mathit {G}}(\Gamma _1) \cap \partial \Theta _{\mathit {G}}(\Gamma _2) = \operatorname {\mathcal {S}}_{\Gamma _1}\cap \operatorname {\mathcal {S}}_{\Gamma _2}$ provided conditions (1) in Theorems 4.30 and 4.31 hold. Moreover,
$\partial \Theta _{\mathit {G}}(\Gamma _1) \cap \partial \Theta _{\mathit {G}}(\Gamma _2) = \operatorname {\mathcal {S}}_{\Gamma _1}\cap \operatorname {\mathcal {S}}_{\Gamma _2}$ provided conditions (1) in Theorems 4.30 and 4.31 hold. Moreover, ![]() $\Gamma _1$ and
$\Gamma _1$ and ![]() $\Gamma _2$ satisfy (R) and (R
$\Gamma _2$ satisfy (R) and (R![]() $_\star$) for some slope
$_\star$) for some slope ![]() $s$ if and only if
$s$ if and only if ![]() $\operatorname {HF}(\gamma _1,\gamma _2)=0$ for all
$\operatorname {HF}(\gamma _1,\gamma _2)=0$ for all ![]() $\gamma _1\in \Gamma _1$ and
$\gamma _1\in \Gamma _1$ and ![]() $\gamma _2\in \Gamma _2$ of slope
$\gamma _2\in \Gamma _2$ of slope ![]() $s$ by Lemma 4.20. Thus, by Theorem 3.5, it suffices to show that
$s$ by Lemma 4.20. Thus, by Theorem 3.5, it suffices to show that ![]() $\operatorname {HF}(\Gamma _1,\Gamma _2)$ is
$\operatorname {HF}(\Gamma _1,\Gamma _2)$ is ![]() $G$-thin if and only if:
$G$-thin if and only if:
(1)
 $\Theta _{\mathit {G}}(\Gamma _1) \cup \Theta _{\mathit {G}}(\Gamma _2) = \operatorname {\mathbb {Q}P}^1$; and
$\Theta _{\mathit {G}}(\Gamma _1) \cup \Theta _{\mathit {G}}(\Gamma _2) = \operatorname {\mathbb {Q}P}^1$; and(2′) for every slope
 $s\in \operatorname {\mathcal {S}}_{\Gamma _1} \cap \operatorname {\mathcal {S}}_{\Gamma _2}$,
$s\in \operatorname {\mathcal {S}}_{\Gamma _1} \cap \operatorname {\mathcal {S}}_{\Gamma _2}$,  $\operatorname {HF}(\gamma _1,\gamma _2)=0$ for all
$\operatorname {HF}(\gamma _1,\gamma _2)=0$ for all  $\gamma _1\in \Gamma _1$ and
$\gamma _1\in \Gamma _1$ and  $\gamma _2\in \Gamma _2$ of slope
$\gamma _2\in \Gamma _2$ of slope  $s$.
$s$.
We now go through the same case-by-case analysis depending on ![]() $\operatorname {\mathcal {S}}_{\Gamma _1}$ and
$\operatorname {\mathcal {S}}_{\Gamma _1}$ and ![]() $\operatorname {\mathcal {S}}_{\Gamma _2}$ as in the proof of Theorem 2.14. Here
$\operatorname {\mathcal {S}}_{\Gamma _2}$ as in the proof of Theorem 2.14. Here ![]() $\Gamma _1$ will play the role of
$\Gamma _1$ will play the role of ![]() $C$ and
$C$ and ![]() $\Gamma _2$ will play the role of
$\Gamma _2$ will play the role of ![]() $D$. Clearly, if
$D$. Clearly, if ![]() $\operatorname {HF}(\Gamma _1,\Gamma _2)$ is
$\operatorname {HF}(\Gamma _1,\Gamma _2)$ is ![]() $G$-thin, then condition (2
$G$-thin, then condition (2![]() $'$) holds. Thus, let us assume this condition from now on. It plays the same role as condition (2
$'$) holds. Thus, let us assume this condition from now on. It plays the same role as condition (2![]() $'$) in the proof of Theorem 2.14.
$'$) in the proof of Theorem 2.14.
Case 0: ![]() $\operatorname {\mathcal {S}}_{\Gamma _1}\cap \operatorname {\mathcal {S}}_{\Gamma _2}=\varnothing$. The original proof goes through unchanged.
$\operatorname {\mathcal {S}}_{\Gamma _1}\cap \operatorname {\mathcal {S}}_{\Gamma _2}=\varnothing$. The original proof goes through unchanged.
Case 1: ![]() $\operatorname {\mathcal {S}}_{\Gamma _1}\cap \operatorname {\mathcal {S}}_{\Gamma _2}=\{s\}$. (a) The case
$\operatorname {\mathcal {S}}_{\Gamma _1}\cap \operatorname {\mathcal {S}}_{\Gamma _2}=\{s\}$. (a) The case ![]() $\operatorname {\mathcal {S}}_{\Gamma _1}=\operatorname {\mathcal {S}}_{\Gamma _2}=\{s\}$ goes through unchanged, because both curves contain some non-inhibited rational component.
$\operatorname {\mathcal {S}}_{\Gamma _1}=\operatorname {\mathcal {S}}_{\Gamma _2}=\{s\}$ goes through unchanged, because both curves contain some non-inhibited rational component.
(b) Suppose ![]() $\operatorname {\mathcal {S}}_{\Gamma _1}=\{s\}$ and
$\operatorname {\mathcal {S}}_{\Gamma _1}=\{s\}$ and ![]() $\operatorname {\mathcal {S}}_{\Gamma _2}\supsetneq \{s\}$. The argument from the original proof can be adapted as follows: if
$\operatorname {\mathcal {S}}_{\Gamma _2}\supsetneq \{s\}$. The argument from the original proof can be adapted as follows: if ![]() $\Gamma _1$ contains curves of different
$\Gamma _1$ contains curves of different ![]() $\delta$-gradings, the statements on either side of the asserted equivalence are wrong. If all components of
$\delta$-gradings, the statements on either side of the asserted equivalence are wrong. If all components of ![]() $\Gamma _1$ have the same
$\Gamma _1$ have the same ![]() $\delta$-grading,
$\delta$-grading, ![]() $\Theta _{\mathit {G}}(\Gamma _1)=\operatorname {\mathbb {Q}P}^1\smallsetminus \{s\}$, so condition (1) is equivalent to
$\Theta _{\mathit {G}}(\Gamma _1)=\operatorname {\mathbb {Q}P}^1\smallsetminus \{s\}$, so condition (1) is equivalent to ![]() $s\in \Theta _{\mathit {G}}(\Gamma _2)$. Since
$s\in \Theta _{\mathit {G}}(\Gamma _2)$. Since ![]() $\Gamma _1$ is non-trivial, it contains some non-inhibited rational component of slope
$\Gamma _1$ is non-trivial, it contains some non-inhibited rational component of slope ![]() $s$. By Lemma 4.22 and assumption (2
$s$. By Lemma 4.22 and assumption (2![]() $'$),
$'$), ![]() $\Gamma _2$ is
$\Gamma _2$ is ![]() $s$-inhibited. Thus,
$s$-inhibited. Thus, ![]() $s\in \Theta _{\mathit {G}}(\Gamma _2)$ is equivalent to
$s\in \Theta _{\mathit {G}}(\Gamma _2)$ is equivalent to ![]() $\delta (\mathbf {r}(s),\gamma )\in G$ being constant for all components
$\delta (\mathbf {r}(s),\gamma )\in G$ being constant for all components ![]() $\gamma \in \Gamma _2$ of slope different from
$\gamma \in \Gamma _2$ of slope different from ![]() $s$. Still assuming condition (2
$s$. Still assuming condition (2![]() $'$) holds, this is equivalent to
$'$) holds, this is equivalent to ![]() $\operatorname {HF}(\Gamma _1,\Gamma _2)$ being thin.
$\operatorname {HF}(\Gamma _1,\Gamma _2)$ being thin.
(c) Suppose ![]() $\operatorname {\mathcal {S}}_{\Gamma _1}\supsetneq \{s\}$ and
$\operatorname {\mathcal {S}}_{\Gamma _1}\supsetneq \{s\}$ and ![]() $\operatorname {\mathcal {S}}_{\Gamma _2}=\{s\}$. This is the same as Case 1(b) with reversed roles of
$\operatorname {\mathcal {S}}_{\Gamma _2}=\{s\}$. This is the same as Case 1(b) with reversed roles of ![]() $\Gamma _1$ and
$\Gamma _1$ and ![]() $\Gamma _2$.
$\Gamma _2$.
(d) Suppose ![]() $|\operatorname {\mathcal {S}}_{\Gamma _i}|>1$ for
$|\operatorname {\mathcal {S}}_{\Gamma _i}|>1$ for ![]() $i=1,2$. The proof in this case goes through unchanged, noting that condition (2
$i=1,2$. The proof in this case goes through unchanged, noting that condition (2![]() $'$) implies that if
$'$) implies that if ![]() $(s,t_1)\subseteq \Theta _{\mathit {G}}(\Gamma _2)$ and
$(s,t_1)\subseteq \Theta _{\mathit {G}}(\Gamma _2)$ and ![]() $(s_m,s)\subseteq \Theta _{\mathit {G}}(\Gamma _1)$, then also
$(s_m,s)\subseteq \Theta _{\mathit {G}}(\Gamma _1)$, then also ![]() $s\in \Theta _{\mathit {G}}(\Gamma _1)\cup \Theta _{\mathit {G}}(\Gamma _2)$, since at least one of
$s\in \Theta _{\mathit {G}}(\Gamma _1)\cup \Theta _{\mathit {G}}(\Gamma _2)$, since at least one of ![]() $\Gamma _1$ and
$\Gamma _1$ and ![]() $\Gamma _2$ is
$\Gamma _2$ is ![]() $s$-inhibited.
$s$-inhibited.
Case 2: ![]() $\operatorname {\mathcal {S}}_{\Gamma _1}\cap \operatorname {\mathcal {S}}_{\Gamma _2}=\{s,t\}$. (a) Suppose that
$\operatorname {\mathcal {S}}_{\Gamma _1}\cap \operatorname {\mathcal {S}}_{\Gamma _2}=\{s,t\}$. (a) Suppose that ![]() $|\operatorname {\mathcal {S}}_{\Gamma _i}|=2$ for
$|\operatorname {\mathcal {S}}_{\Gamma _i}|=2$ for ![]() $i=1,2$. Most of the proof in this case goes through unchanged. It only remains to see that
$i=1,2$. Most of the proof in this case goes through unchanged. It only remains to see that ![]() $\Theta _{\mathit {G}}(\Gamma _1) \cup \Theta _{\mathit {G}}(\Gamma _2) \supseteq \operatorname {\mathbb {Q}P}^1\smallsetminus \{s,t\}$ implies that also
$\Theta _{\mathit {G}}(\Gamma _1) \cup \Theta _{\mathit {G}}(\Gamma _2) \supseteq \operatorname {\mathbb {Q}P}^1\smallsetminus \{s,t\}$ implies that also ![]() $s,t\in \Theta _{\mathit {G}}(\Gamma _1)\cup \Theta _{\mathit {G}}(\Gamma _2)$, under the assumption that condition (2
$s,t\in \Theta _{\mathit {G}}(\Gamma _1)\cup \Theta _{\mathit {G}}(\Gamma _2)$, under the assumption that condition (2![]() $'$) holds. Indeed, the inclusion implies that
$'$) holds. Indeed, the inclusion implies that ![]() $\Theta _{\mathit {G}}(\Gamma _1)$ and
$\Theta _{\mathit {G}}(\Gamma _1)$ and ![]() $\Theta _{\mathit {G}}(\Gamma _2)$ are intervals with endpoints equal to
$\Theta _{\mathit {G}}(\Gamma _2)$ are intervals with endpoints equal to ![]() $s$ and
$s$ and ![]() $t$. Now suppose for contradiction that
$t$. Now suppose for contradiction that ![]() $s\not \in \Theta _{\mathit {G}}(\Gamma _1)\cup \Theta _{\mathit {G}}(\Gamma _2)$. Then there exist non-inhibited rational components
$s\not \in \Theta _{\mathit {G}}(\Gamma _1)\cup \Theta _{\mathit {G}}(\Gamma _2)$. Then there exist non-inhibited rational components ![]() $\gamma _1\in \Gamma _1$ and
$\gamma _1\in \Gamma _1$ and ![]() $\gamma _2\in \Gamma _2$ of slope
$\gamma _2\in \Gamma _2$ of slope ![]() $s$. However, this violates condition (2
$s$. However, this violates condition (2![]() $'$) according to Lemma 4.22. The same argument works if we replace
$'$) according to Lemma 4.22. The same argument works if we replace ![]() $s$ by
$s$ by ![]() $t$.
$t$.
(b) Suppose ![]() $|\operatorname {\mathcal {S}}_{\Gamma _1}|>2$. The original argument goes through unchanged, using the same observation as in Case 2(a).
$|\operatorname {\mathcal {S}}_{\Gamma _1}|>2$. The original argument goes through unchanged, using the same observation as in Case 2(a).
(c) Suppose ![]() $|\operatorname {\mathcal {S}}_{\Gamma _2}|>2$. Same as Case 2(b) with reversed roles of
$|\operatorname {\mathcal {S}}_{\Gamma _2}|>2$. Same as Case 2(b) with reversed roles of ![]() $\Gamma _1$ and
$\Gamma _1$ and ![]() $\Gamma _2$.
$\Gamma _2$.
Case 3: ![]() $|\operatorname {\mathcal {S}}_{\Gamma _1}\cap \operatorname {\mathcal {S}}_{\Gamma _2}|>2$. This case goes through unchanged.
$|\operatorname {\mathcal {S}}_{\Gamma _1}\cap \operatorname {\mathcal {S}}_{\Gamma _2}|>2$. This case goes through unchanged.
5. The tangle invariant  $\widetilde {\operatorname {Kh}}$
$\widetilde {\operatorname {Kh}}$
In this section, we review some properties of the immersed curve invariant ![]() $\widetilde {\operatorname {Kh}}$ of Conway tangles from [Reference Kotelskiy, Watson and ZibrowiusKWZ19]. We work exclusively over the field
$\widetilde {\operatorname {Kh}}$ of Conway tangles from [Reference Kotelskiy, Watson and ZibrowiusKWZ19]. We work exclusively over the field ![]() $\mathbb {F}$ of two elements, with remarks about other coefficient systems when appropriate.
$\mathbb {F}$ of two elements, with remarks about other coefficient systems when appropriate.
5.1 The definition of  $\widetilde {\operatorname {Kh}}$
$\widetilde {\operatorname {Kh}}$
Let ![]() $T$ be an oriented pointed Conway tangle, that is a Conway tangle
$T$ be an oriented pointed Conway tangle, that is a Conway tangle ![]() $T$ in the three-ball
$T$ in the three-ball ![]() $B^3$ with a choice of distinguished tangle end, which we usually mark by
$B^3$ with a choice of distinguished tangle end, which we usually mark by ![]() $\ast$. With such a tangle, we associate an invariant
$\ast$. With such a tangle, we associate an invariant ![]() $\widetilde {\operatorname {Kh}}(T)$, which takes the form of a collection of immersed curves with local systems on the boundary of
$\widetilde {\operatorname {Kh}}(T)$, which takes the form of a collection of immersed curves with local systems on the boundary of ![]() $B^3$ minus the four tangle ends. Like
$B^3$ minus the four tangle ends. Like ![]() $\operatorname {HFT}(T)$, these immersed curves with local systems are defined in two steps, which we sketch below.
$\operatorname {HFT}(T)$, these immersed curves with local systems are defined in two steps, which we sketch below.
First, one fixes a diagram ![]() $\mathcal {D}_T$ of the pointed tangle
$\mathcal {D}_T$ of the pointed tangle ![]() $T$. Bar-Natan associates with such a diagram a bigraded chain complex
$T$. Bar-Natan associates with such a diagram a bigraded chain complex ![]() ${[\![ \mathcal {D}_T ]\!]}_{/l}$ over a certain cobordism category
${[\![ \mathcal {D}_T ]\!]}_{/l}$ over a certain cobordism category ![]() $\operatorname {\operatorname {Cob}_{/{\mathit {l}}}}$, whose objects are crossingless tangle diagrams [Reference Bar-NatanBN05]. This complex is a tangle invariant up to bigraded chain homotopy, and thus is frequently denoted by
$\operatorname {\operatorname {Cob}_{/{\mathit {l}}}}$, whose objects are crossingless tangle diagrams [Reference Bar-NatanBN05]. This complex is a tangle invariant up to bigraded chain homotopy, and thus is frequently denoted by ![]() ${[\![ T ]\!]}_{/l}$. Thanks to a process Bar-Natan calls delooping [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Observation 4.18], any chain complex over
${[\![ T ]\!]}_{/l}$. Thanks to a process Bar-Natan calls delooping [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Observation 4.18], any chain complex over ![]() $\operatorname {\operatorname {Cob}_{/{\mathit {l}}}}$ can be written as a chain complex over the full subcategory
$\operatorname {\operatorname {Cob}_{/{\mathit {l}}}}$ can be written as a chain complex over the full subcategory ![]() of
of ![]() $\operatorname {\operatorname {Cob}_{/{\mathit {l}}}}$ generated by the crossingless tangles without closed components. This subcategory is isomorphic to the following quiver algebra [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Theorem 1.1].
$\operatorname {\operatorname {Cob}_{/{\mathit {l}}}}$ generated by the crossingless tangles without closed components. This subcategory is isomorphic to the following quiver algebra [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Theorem 1.1].

The objects ![]() and
and ![]() correspond to
correspond to ![]() $\bullet$ and
$\bullet$ and ![]() $\circ$, respectively. We denote the idempotent constant paths on
$\circ$, respectively. We denote the idempotent constant paths on ![]() $\bullet$ and
$\bullet$ and ![]() $\circ$ by
$\circ$ by ![]() $\iota _{\bullet }$ and
$\iota _{\bullet }$ and ![]() $\iota _{\circ }$, respectively. We will sometimes abuse notation by using
$\iota _{\circ }$, respectively. We will sometimes abuse notation by using ![]() $S$ for either
$S$ for either ![]() ${}_{\circ }S_{\bullet }$ or
${}_{\circ }S_{\bullet }$ or ![]() ${}_{\bullet }S_{\circ }$ and using
${}_{\bullet }S_{\circ }$ and using ![]() $D$ for either
$D$ for either ![]() ${}_{\circ }D_{\circ }$ or
${}_{\circ }D_{\circ }$ or ![]() ${}_{\bullet }D_{\bullet }$. In addition, the subscript
${}_{\bullet }D_{\bullet }$. In addition, the subscript ![]() $\star \in \{\circ,\bullet \}$ on the left or right of an algebra element
$\star \in \{\circ,\bullet \}$ on the left or right of an algebra element ![]() $a$ will always indicate that multiplying by
$a$ will always indicate that multiplying by ![]() $\iota _\star$ from the left or right, respectively, preserves the element
$\iota _\star$ from the left or right, respectively, preserves the element ![]() $a$. This allows shorthand notation such as
$a$. This allows shorthand notation such as ![]() $S_{\circ }={}_{\bullet }S_{\circ }$ and
$S_{\circ }={}_{\bullet }S_{\circ }$ and ![]() $S^3_{\bullet }= {}_{\circ }S_{\bullet } \cdot {}_{\bullet }S_{\circ } \cdot {}_{\circ }S_{\bullet }$. The algebra
$S^3_{\bullet }= {}_{\circ }S_{\bullet } \cdot {}_{\bullet }S_{\circ } \cdot {}_{\circ }S_{\bullet }$. The algebra ![]() $\mathcal {B}$ carries a bigrading: The quantum grading
$\mathcal {B}$ carries a bigrading: The quantum grading ![]() $q$ and the delta grading
$q$ and the delta grading ![]() $\delta$ are determined by
$\delta$ are determined by
Differentials of bigraded chain complexes over ![]() $\mathcal {B}$ are defined to preserve quantum grading and decrease
$\mathcal {B}$ are defined to preserve quantum grading and decrease ![]() $\delta$-grading by 1. The isomorphism
$\delta$-grading by 1. The isomorphism ![]() allows us to translate the delooped chain complex
allows us to translate the delooped chain complex ![]() ${[\![ \mathcal {D}_T ]\!]}_{/l}$ into a bigraded chain complex
${[\![ \mathcal {D}_T ]\!]}_{/l}$ into a bigraded chain complex ![]() ${\unicode{x0414}}(\mathcal {D}_T)$ over
${\unicode{x0414}}(\mathcal {D}_T)$ over ![]() $\mathcal {B}$ (see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Definition 1.2]). (Chain complexes over ordinary algebras have also appeared in the literature under the name of type D structures [Reference Lipshitz, Ozsváth and ThurstonLOT15, Definition 2.2.23], and we therefore use the two terms interchangeably; see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Proposition 2.13] for more on the equivalence of these objects.) By construction, the bigraded chain homotopy type of
$\mathcal {B}$ (see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Definition 1.2]). (Chain complexes over ordinary algebras have also appeared in the literature under the name of type D structures [Reference Lipshitz, Ozsváth and ThurstonLOT15, Definition 2.2.23], and we therefore use the two terms interchangeably; see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Proposition 2.13] for more on the equivalence of these objects.) By construction, the bigraded chain homotopy type of ![]() ${\unicode{x0414}}(\mathcal {D}_T)$ is an invariant of the tangle
${\unicode{x0414}}(\mathcal {D}_T)$ is an invariant of the tangle ![]() $T$, and thus we sometimes write
$T$, and thus we sometimes write ![]() ${\unicode{x0414}}(T)$ for
${\unicode{x0414}}(T)$ for ![]() ${\unicode{x0414}}(\mathcal {D}_T)$. Moreover, using the central element
${\unicode{x0414}}(\mathcal {D}_T)$. Moreover, using the central element
we define a bigraded chain complex ![]() ${\unicode{x0414}}_1(\mathcal {D}_T)$ as the mapping cone
${\unicode{x0414}}_1(\mathcal {D}_T)$ as the mapping cone
where ![]() $H\cdot \operatorname {id} (x) = x\otimes H$ for every generator
$H\cdot \operatorname {id} (x) = x\otimes H$ for every generator ![]() $x$ in
$x$ in ![]() ${\unicode{x0414}}(\mathcal {D}_T)$. The bigraded chain homotopy type of
${\unicode{x0414}}(\mathcal {D}_T)$. The bigraded chain homotopy type of ![]() ${\unicode{x0414}}_1(\mathcal {D}_T)$ is also a tangle invariant, and we write
${\unicode{x0414}}_1(\mathcal {D}_T)$ is also a tangle invariant, and we write ![]() ${\unicode{x0414}}_1(T)$ for
${\unicode{x0414}}_1(T)$ for ![]() ${\unicode{x0414}}_1(\mathcal {D}_T)$.
${\unicode{x0414}}_1(\mathcal {D}_T)$.
The second step in the definition of ![]() $\widetilde {\operatorname {Kh}}(T)$ relies on a classification result, similar to that used in the definition of
$\widetilde {\operatorname {Kh}}(T)$ relies on a classification result, similar to that used in the definition of ![]() $\operatorname {HFT}(T)$. This classification result says that the chain homotopy classes of bigraded chain complexes over
$\operatorname {HFT}(T)$. This classification result says that the chain homotopy classes of bigraded chain complexes over ![]() $\mathcal {B}$ are in one-to-one correspondence with free homotopy classes of bigraded immersed multicurves with local systems on the four-punctured sphere
$\mathcal {B}$ are in one-to-one correspondence with free homotopy classes of bigraded immersed multicurves with local systems on the four-punctured sphere ![]() $S^2_{4,\ast }$, where the latter has one special puncture distinguished by
$S^2_{4,\ast }$, where the latter has one special puncture distinguished by ![]() $\ast$ (see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Theorem 1.5]). In contrast to the
$\ast$ (see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Theorem 1.5]). In contrast to the ![]() $\operatorname {HFT}(T)$ setting, here ‘immersed curves’ also include non-compact curves, that is non-null-homotopic immersions of intervals into the four-punctured sphere, with ends on the three non-special punctures of
$\operatorname {HFT}(T)$ setting, here ‘immersed curves’ also include non-compact curves, that is non-null-homotopic immersions of intervals into the four-punctured sphere, with ends on the three non-special punctures of ![]() $S^2_{4,\ast }$; see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Definition 1.4]. As in the
$S^2_{4,\ast }$; see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Definition 1.4]. As in the ![]() $\operatorname {HFT}(T)$ setting, the correspondence between chain complexes and immersed multicurves uses a parametrization of
$\operatorname {HFT}(T)$ setting, the correspondence between chain complexes and immersed multicurves uses a parametrization of ![]() $S^2_{4,\ast }$. This time, the parametrization is given by the two dotted arcs shown in Figure 13(c). We generally assume that the multicurves intersect these arcs minimally. Then, roughly speaking, the intersection points correspond to generators of the according chain complexes and paths between those intersection points correspond to the differentials. This is illustrated in Figure 12, cf. [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Example 1.6].
$S^2_{4,\ast }$. This time, the parametrization is given by the two dotted arcs shown in Figure 13(c). We generally assume that the multicurves intersect these arcs minimally. Then, roughly speaking, the intersection points correspond to generators of the according chain complexes and paths between those intersection points correspond to the differentials. This is illustrated in Figure 12, cf. [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Example 1.6].

Figure 12. The geometric interpretation of some chain complexes over the algebra ![]() $\mathcal {B}$ illustrating the classification theorem in the second part of the construction of
$\mathcal {B}$ illustrating the classification theorem in the second part of the construction of ![]() $\widetilde {\operatorname {BN}}(T)$ and
$\widetilde {\operatorname {BN}}(T)$ and ![]() $\widetilde {\operatorname {Kh}}(T)$.
$\widetilde {\operatorname {Kh}}(T)$.

Figure 13. The Khovanov and Bar-Natan invariant of the pretzel tangle from Figure 5.
Finally, the multicurve invariant ![]() $\widetilde {\operatorname {Kh}}(T)$ is defined as the collection of bigraded immersed curves on
$\widetilde {\operatorname {Kh}}(T)$ is defined as the collection of bigraded immersed curves on ![]() $S^2_{4,\ast }$ that corresponds to
$S^2_{4,\ast }$ that corresponds to ![]() ${\unicode{x0414}}_1(T)$. Similarly, the type D structure
${\unicode{x0414}}_1(T)$. Similarly, the type D structure ![]() ${\unicode{x0414}}(T)$ corresponds to a multicurve that we denote by
${\unicode{x0414}}(T)$ corresponds to a multicurve that we denote by ![]() $\widetilde {\operatorname {BN}}(T)$. Examples are shown in Figure 12. Whereas
$\widetilde {\operatorname {BN}}(T)$. Examples are shown in Figure 12. Whereas ![]() $\widetilde {\operatorname {Kh}}(T)$ only consists of compact curves, i.e. immersed circles,
$\widetilde {\operatorname {Kh}}(T)$ only consists of compact curves, i.e. immersed circles, ![]() $\widetilde {\operatorname {BN}}(T)$ also contains
$\widetilde {\operatorname {BN}}(T)$ also contains ![]() $2^{|T|}$ non-compact components, where
$2^{|T|}$ non-compact components, where ![]() $|T|$ is the number of closed components of
$|T|$ is the number of closed components of ![]() $T$.
$T$.
Remark 5.1 (Coefficients)
In general, the construction of the tangle invariants ![]() ${\unicode{x0414}}(T)$ and
${\unicode{x0414}}(T)$ and ![]() ${\unicode{x0414}}_1(T)$ can be done over
${\unicode{x0414}}_1(T)$ can be done over ![]() $\mathbb {Z}$. The classification result works over arbitrary fields, and hence so does the construction of the immersed curve invariants. However, in this paper,
$\mathbb {Z}$. The classification result works over arbitrary fields, and hence so does the construction of the immersed curve invariants. However, in this paper, ![]() $\widetilde {\operatorname {BN}}(T)$ and
$\widetilde {\operatorname {BN}}(T)$ and ![]() $\widetilde {\operatorname {Kh}}(T)$ always denote the curves over
$\widetilde {\operatorname {Kh}}(T)$ always denote the curves over ![]() $\mathbb {F}$, unless stated otherwise.
$\mathbb {F}$, unless stated otherwise.
One can identify ![]() $S^2_{4,\ast }$ with
$S^2_{4,\ast }$ with ![]() $\partial B^3\smallsetminus \partial T$ using the parametrization of the latter shown in Figure 13(a). This identification is natural in the same sense as for
$\partial B^3\smallsetminus \partial T$ using the parametrization of the latter shown in Figure 13(a). This identification is natural in the same sense as for ![]() $\operatorname {HFT}(T)$, see Theorem 3.1, provided we work over
$\operatorname {HFT}(T)$, see Theorem 3.1, provided we work over ![]() $\mathbb {F}$ (see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Theorem 1.13]). We expect the same to hold over arbitrary fields.
$\mathbb {F}$ (see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Theorem 1.13]). We expect the same to hold over arbitrary fields.
Theorem 5.2 For all ![]() $\tau \in \operatorname {Mod}(S^2_4)$,
$\tau \in \operatorname {Mod}(S^2_4)$, ![]() $\widetilde {\operatorname {Kh}}(\tau (T)) = \tau (\widetilde {\operatorname {Kh}}(T))$ and
$\widetilde {\operatorname {Kh}}(\tau (T)) = \tau (\widetilde {\operatorname {Kh}}(T))$ and ![]() $\widetilde {\operatorname {BN}}(\tau (T)) = \tau (\widetilde {\operatorname {BN}}(T))$.
$\widetilde {\operatorname {BN}}(\tau (T)) = \tau (\widetilde {\operatorname {BN}}(T))$.
Remark 5.3 When working over ![]() $\mathbb {F}$, the distinguished tangle end
$\mathbb {F}$, the distinguished tangle end ![]() $\ast$ only plays a role in the second step of the construction of
$\ast$ only plays a role in the second step of the construction of ![]() $\widetilde {\operatorname {BN}}(T)$ and
$\widetilde {\operatorname {BN}}(T)$ and ![]() $\widetilde {\operatorname {Kh}}(T)$. If one works away from characteristic 2, it also plays a subtle role in the first step: In this case, there are four different isomorphisms between
$\widetilde {\operatorname {Kh}}(T)$. If one works away from characteristic 2, it also plays a subtle role in the first step: In this case, there are four different isomorphisms between ![]() and
and ![]() $\mathcal {B}$, which only differ by the signs on the basic morphisms
$\mathcal {B}$, which only differ by the signs on the basic morphisms ![]() $D_{\bullet }$ and
$D_{\bullet }$ and ![]() $D_{\circ }$. Each of these isomorphisms corresponds to a choice of distinguished tangle end; see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Theorem 4.21, Observation 4.24] for details.
$D_{\circ }$. Each of these isomorphisms corresponds to a choice of distinguished tangle end; see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Theorem 4.21, Observation 4.24] for details.
Example 5.4 We usually draw the four-punctured sphere ![]() $S^2_{4,\ast }$ as the plane plus a point at infinity minus the four punctures and indicate its standard parametrization that identifies
$S^2_{4,\ast }$ as the plane plus a point at infinity minus the four punctures and indicate its standard parametrization that identifies ![]() $S^2_{4,\ast }$ with
$S^2_{4,\ast }$ with ![]() $\partial B^3\smallsetminus \partial T$ by two dotted arcs as in Figures 13(b) and 13(c). The solid and dashed curves in these figures show
$\partial B^3\smallsetminus \partial T$ by two dotted arcs as in Figures 13(b) and 13(c). The solid and dashed curves in these figures show ![]() $\widetilde {\operatorname {BN}}(P_{2,-3})$ and
$\widetilde {\operatorname {BN}}(P_{2,-3})$ and ![]() $\widetilde {\operatorname {Kh}}(P_{2,-3})$, respectively, where
$\widetilde {\operatorname {Kh}}(P_{2,-3})$, respectively, where ![]() $P_{2,-3}$ is the
$P_{2,-3}$ is the ![]() $(2,-3)$-pretzel tangle from Figure 13(a), cf. [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Example 6.7]. All components of these curves carry the (unique) one-dimensional local system over
$(2,-3)$-pretzel tangle from Figure 13(a), cf. [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Example 6.7]. All components of these curves carry the (unique) one-dimensional local system over ![]() $\mathbb {F}$.
$\mathbb {F}$.
Example 5.5 For any slope ![]() $s\in \operatorname {\mathbb {Q}P}^1$,
$s\in \operatorname {\mathbb {Q}P}^1$, ![]() $\widetilde {\operatorname {BN}}(Q_s)$ consists of a single arc which is obtained by pushing the tangle strand that does not end on the distinguished tangle end
$\widetilde {\operatorname {BN}}(Q_s)$ consists of a single arc which is obtained by pushing the tangle strand that does not end on the distinguished tangle end ![]() $\ast$ onto
$\ast$ onto ![]() $S^2_{4,\ast }$. Here
$S^2_{4,\ast }$. Here ![]() $\widetilde {\operatorname {Kh}}(Q_s)$ is equal to a figure-eight curve that lies in a small neighborhood of
$\widetilde {\operatorname {Kh}}(Q_s)$ is equal to a figure-eight curve that lies in a small neighborhood of ![]() $\widetilde {\operatorname {BN}}(Q_s)$ and encloses the two tangle ends on either side, see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Example 6.6]. The local system on this curve is one-dimensional. We expect that over arbitrary fields, the underlying curve for
$\widetilde {\operatorname {BN}}(Q_s)$ and encloses the two tangle ends on either side, see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Example 6.6]. The local system on this curve is one-dimensional. We expect that over arbitrary fields, the underlying curve for ![]() $\widetilde {\operatorname {Kh}}(Q_s)$ is the same as over
$\widetilde {\operatorname {Kh}}(Q_s)$ is the same as over ![]() $\mathbb {F}$, and that the local systems on these curves are equal to
$\mathbb {F}$, and that the local systems on these curves are equal to ![]() $(-1)$.
$(-1)$.
In particular, ![]() $\widetilde {\operatorname {Kh}}(Q_s)$ is not embedded, unlike
$\widetilde {\operatorname {Kh}}(Q_s)$ is not embedded, unlike ![]() $\operatorname {HFT}(Q_s)$. In fact, we have the following [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Proposition 6.18], over any field.
$\operatorname {HFT}(Q_s)$. In fact, we have the following [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Proposition 6.18], over any field.
Proposition 5.6 For any pointed Conway tangle ![]() $T$, no component of
$T$, no component of ![]() $\widetilde {\operatorname {Kh}}(T)$ is embedded.
$\widetilde {\operatorname {Kh}}(T)$ is embedded.
Like ![]() $\operatorname {HFT}$, the tangle invariants in Khovanov theory detect rational tangles.
$\operatorname {HFT}$, the tangle invariants in Khovanov theory detect rational tangles.
Theorem 5.7 A tangle ![]() $T$ is rational if and only if
$T$ is rational if and only if ![]() $\widetilde {\operatorname {Kh}}(T)$ consists of a single figure-eight curve carrying the unique one-dimensional local system.
$\widetilde {\operatorname {Kh}}(T)$ consists of a single figure-eight curve carrying the unique one-dimensional local system.
Proof. This follows from essentially the same arguments as [Reference ZibrowiusZib20, Theorem 6.2]. More generally, any tangle invariant detects rational tangles, as long as the tangle invariant satisfies a gluing theorem to a link invariant that detects the two-component unlink. The gluing theorem for ![]() $\widetilde {\operatorname {Kh}}$ is Theorem 5.8. The requisite detection result was proven by Hedden and Ni [Reference Hedden and NiHN10], based on Kronheimer and Mrowka's unknot detection of Khovanov homology [Reference Kronheimer and MrowkaKM11].
$\widetilde {\operatorname {Kh}}$ is Theorem 5.8. The requisite detection result was proven by Hedden and Ni [Reference Hedden and NiHN10], based on Kronheimer and Mrowka's unknot detection of Khovanov homology [Reference Kronheimer and MrowkaKM11].
5.2 A gluing theorem for  $\widetilde {\operatorname {Kh}}$
$\widetilde {\operatorname {Kh}}$
Denote the two-dimensional vector space supported in ![]() $\delta$-grading
$\delta$-grading ![]() $+\tfrac {1}{2}$ and quantum gradings
$+\tfrac {1}{2}$ and quantum gradings ![]() $\pm 1$ by
$\pm 1$ by
Theorem 5.8 [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Theorem 1.9]
Let ![]() $L=T_1\cup T_2$ be the result of gluing two oriented pointed Conway tangles as in Figure 1 such that the orientations match. Let
$L=T_1\cup T_2$ be the result of gluing two oriented pointed Conway tangles as in Figure 1 such that the orientations match. Let ![]() $T^*_1$ be the mirror image of
$T^*_1$ be the mirror image of ![]() $T_1$ with the orientation of all components reversed. Then
$T_1$ with the orientation of all components reversed. Then
 \begin{gather*} \widetilde{\operatorname{Kh}}(L)\otimes V\cong \operatorname{HF}(\widetilde{\operatorname{Kh}}(T^*_1),\widetilde{\operatorname{Kh}}(T_2)), \\ \widetilde{\operatorname{Kh}}(L)\cong \operatorname{HF}(\widetilde{\operatorname{Kh}}(T_1^*),\widetilde{\operatorname{BN}}(T_2)) \end{gather*}
\begin{gather*} \widetilde{\operatorname{Kh}}(L)\otimes V\cong \operatorname{HF}(\widetilde{\operatorname{Kh}}(T^*_1),\widetilde{\operatorname{Kh}}(T_2)), \\ \widetilde{\operatorname{Kh}}(L)\cong \operatorname{HF}(\widetilde{\operatorname{Kh}}(T_1^*),\widetilde{\operatorname{BN}}(T_2)) \end{gather*}
as relatively bigraded ![]() ${\mathbb {F}}$-vector spaces.
${\mathbb {F}}$-vector spaces.
One can easily compute ![]() $\widetilde {\operatorname {Kh}}(T^*_1)$ from
$\widetilde {\operatorname {Kh}}(T^*_1)$ from ![]() $\widetilde {\operatorname {Kh}}(T_1)$ (see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Proposition 7.1]). For this, let
$\widetilde {\operatorname {Kh}}(T_1)$ (see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Proposition 7.1]). For this, let ![]() $\operatorname {m}$ denote the mirror operation, i.e. the involution of the four-punctured sphere that fixes the four punctures pointwise, fixes the parametrizing arcs setwise, and interchanges the front and back, as in § 3.
$\operatorname {m}$ denote the mirror operation, i.e. the involution of the four-punctured sphere that fixes the four punctures pointwise, fixes the parametrizing arcs setwise, and interchanges the front and back, as in § 3.
Lemma 5.9 For any pointed Conway tangle ![]() $T$,
$T$, ![]() $\widetilde {\operatorname {Kh}}(T^*)=\operatorname {m}(\widetilde {\operatorname {Kh}}(T))$ up to an appropriate bigrading shift.
$\widetilde {\operatorname {Kh}}(T^*)=\operatorname {m}(\widetilde {\operatorname {Kh}}(T))$ up to an appropriate bigrading shift.
Remark 5.10 Shumakovitch showed that over ![]() $\mathbb {F}$ the unreduced Khovanov homology of a link splits into two copies of reduced Khovanov homology, whose
$\mathbb {F}$ the unreduced Khovanov homology of a link splits into two copies of reduced Khovanov homology, whose ![]() $\delta$-gradings differ by one [Reference ShumakovitchShu14]. Theorem 5.8 does not compute the unreduced Khovanov homology; instead we have that the
$\delta$-gradings differ by one [Reference ShumakovitchShu14]. Theorem 5.8 does not compute the unreduced Khovanov homology; instead we have that the ![]() $\delta$-gradings of the two copies of reduced Khovanov homology are identical. To obtain unreduced Khovanov homology, one can use yet another immersed curve invariant, namely
$\delta$-gradings of the two copies of reduced Khovanov homology are identical. To obtain unreduced Khovanov homology, one can use yet another immersed curve invariant, namely ![]() $\operatorname {Kh}(T)$, which we introduced in [Reference Kotelskiy, Watson and ZibrowiusKWZ19] and which satisfies analogous gluing theorems.
$\operatorname {Kh}(T)$, which we introduced in [Reference Kotelskiy, Watson and ZibrowiusKWZ19] and which satisfies analogous gluing theorems.
5.3 The geography problem for  $\widetilde {\operatorname {Kh}}$
$\widetilde {\operatorname {Kh}}$
Just as for ![]() $\operatorname {HFT}$, it is often useful to consider the multicurves
$\operatorname {HFT}$, it is often useful to consider the multicurves ![]() $\widetilde {\operatorname {Kh}}$ and
$\widetilde {\operatorname {Kh}}$ and ![]() $\widetilde {\operatorname {BN}}$ in the covering space
$\widetilde {\operatorname {BN}}$ in the covering space ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ of the (now pointed) four-punctured sphere
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ of the (now pointed) four-punctured sphere ![]() $S^2_{4,\ast }$. This covering space is illustrated in Figures 13(d) and 13(e), where the parametrization of
$S^2_{4,\ast }$. This covering space is illustrated in Figures 13(d) and 13(e), where the parametrization of ![]() $S^2_{4,\ast }$ has been lifted to
$S^2_{4,\ast }$ has been lifted to ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ and the two non-adjacent faces and their preimages under the covering map are shaded gray. The two figures also include the lifts of the components of
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ and the two non-adjacent faces and their preimages under the covering map are shaded gray. The two figures also include the lifts of the components of ![]() $\widetilde {\operatorname {BN}}(P_{2,-3})$ and
$\widetilde {\operatorname {BN}}(P_{2,-3})$ and ![]() $\widetilde {\operatorname {Kh}}(P_{2,-3})$, respectively. Note that for
$\widetilde {\operatorname {Kh}}(P_{2,-3})$, respectively. Note that for ![]() $\widetilde {\operatorname {Kh}}(P_{2,-3})$, the lift of each component can be isotoped into an arbitrarily small neighborhood of a straight line of some rational slope
$\widetilde {\operatorname {Kh}}(P_{2,-3})$, the lift of each component can be isotoped into an arbitrarily small neighborhood of a straight line of some rational slope ![]() ${p}/{q}\in \operatorname {\mathbb {Q}P}^1$ going through some punctures. In fact, this is true in general for the invariant
${p}/{q}\in \operatorname {\mathbb {Q}P}^1$ going through some punctures. In fact, this is true in general for the invariant ![]() $\widetilde {\operatorname {Kh}}(T)$.
$\widetilde {\operatorname {Kh}}(T)$.
To make this statement precise, let us consider the following two classes of curves. For ![]() $n\in \mathbb {N}$, let
$n\in \mathbb {N}$, let ![]() $\mathbf {r}_{n}(0)$ and
$\mathbf {r}_{n}(0)$ and ![]() $\mathbf {s}_{2n}(0)$ be the immersed curves in
$\mathbf {s}_{2n}(0)$ be the immersed curves in ![]() $S^2_{4,\ast }$ that admit lifts to the curves
$S^2_{4,\ast }$ that admit lifts to the curves ![]() $\tilde {\mathbf {r}}_{n}(0)$ and
$\tilde {\mathbf {r}}_{n}(0)$ and ![]() $\tilde {\mathbf {s}}_{2n}(0)$, respectively, in Figure 14(d); curves for
$\tilde {\mathbf {s}}_{2n}(0)$, respectively, in Figure 14(d); curves for ![]() $n=1,2,3$ are illustrated in Figures 14(a)–14(c). We refer to the subscripts
$n=1,2,3$ are illustrated in Figures 14(a)–14(c). We refer to the subscripts ![]() $n$, respectively
$n$, respectively ![]() $2n$, as the lengths of those curves. For every slope
$2n$, as the lengths of those curves. For every slope ![]() ${p}/{q}\in \operatorname {\mathbb {Q}P}^1$, we respectively define the curves
${p}/{q}\in \operatorname {\mathbb {Q}P}^1$, we respectively define the curves ![]() $\mathbf {r}_n({p}/{q})$ and
$\mathbf {r}_n({p}/{q})$ and ![]() $\mathbf {s}_{2n}({p}/{q})$ as the images of
$\mathbf {s}_{2n}({p}/{q})$ as the images of ![]() $\mathbf {r}_{n}(0)$ and
$\mathbf {r}_{n}(0)$ and ![]() $\mathbf {s}_{2n}(0)$ under the action of the matrix
$\mathbf {s}_{2n}(0)$ under the action of the matrix
considered as an element the mapping class group ![]() $\operatorname {Mod}(S^2_{4,\ast }) \cong \mathit {PSL}(2,\mathbb {Z})$ consisting of mapping classes fixing the special puncture
$\operatorname {Mod}(S^2_{4,\ast }) \cong \mathit {PSL}(2,\mathbb {Z})$ consisting of mapping classes fixing the special puncture ![]() $\ast$. (This transformation maps straight lines of slope 0 to straight lines of slope
$\ast$. (This transformation maps straight lines of slope 0 to straight lines of slope ![]() ${p}/{q}$. The isomorphism
${p}/{q}$. The isomorphism ![]() $\operatorname {Mod}(S^2_{4,\ast }) \cong \mathit {PSL}(2,\mathbb {Z})$ is induced by the two-fold cover
$\operatorname {Mod}(S^2_{4,\ast }) \cong \mathit {PSL}(2,\mathbb {Z})$ is induced by the two-fold cover ![]() $\mathbb {T}^2 \to S^2_{4,\ast }$ and the isomorphism
$\mathbb {T}^2 \to S^2_{4,\ast }$ and the isomorphism ![]() $\operatorname {Mod}(\mathbb {T}^2) \cong \mathit {SL}(2,\mathbb {Z})$.) The local systems on all these curves are defined to be trivial.
$\operatorname {Mod}(\mathbb {T}^2) \cong \mathit {SL}(2,\mathbb {Z})$.) The local systems on all these curves are defined to be trivial.
Definition 5.11 We call the curves ![]() $\mathbf {r}_{n}({p}/{q})$ rational and the curves
$\mathbf {r}_{n}({p}/{q})$ rational and the curves ![]() $\mathbf {s}_{2n}({p}/{q})$ special. As in the Heegaard Floer setting, given some slope
$\mathbf {s}_{2n}({p}/{q})$ special. As in the Heegaard Floer setting, given some slope ![]() $s\in \operatorname {\mathbb {Q}P}^1$, we call a multicurve
$s\in \operatorname {\mathbb {Q}P}^1$, we call a multicurve ![]() $s$-rational if it does not contain any special component of slope
$s$-rational if it does not contain any special component of slope ![]() $s$, and
$s$, and ![]() $s$-special if it does not contain any rational component of slope
$s$-special if it does not contain any rational component of slope ![]() $s$.
$s$.

Figure 14. The curves ![]() $\mathbf {r}_n(0)$ and
$\mathbf {r}_n(0)$ and ![]() $\mathbf {s}_{2n}(0)$ (a–c) and their lifts to
$\mathbf {s}_{2n}(0)$ (a–c) and their lifts to ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ (d).
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ (d).
Example 5.12 For all slopes ![]() ${p}/{q}\in \operatorname {\mathbb {Q}P}^1$,
${p}/{q}\in \operatorname {\mathbb {Q}P}^1$, ![]() $\widetilde {\operatorname {Kh}}(Q_{p/q})=\mathbf {r}_1({p}/{q})$. Moreover,
$\widetilde {\operatorname {Kh}}(Q_{p/q})=\mathbf {r}_1({p}/{q})$. Moreover, ![]() $\widetilde {\operatorname {Kh}}(P_{2,-3})$ from Figure 13(e) consists of a rational curve of slope
$\widetilde {\operatorname {Kh}}(P_{2,-3})$ from Figure 13(e) consists of a rational curve of slope ![]() ${1}/{2}$ and a special curve of slope
${1}/{2}$ and a special curve of slope ![]() $0$.
$0$.
The following classification result, which is [Reference Kotelskiy, Watson and ZibrowiusKWZ21b, Theorem 1.2], establishes a similar dichotomy between rational and special components of ![]() $\widetilde {\operatorname {Kh}}(T)$ as Theorem 3.9 does for
$\widetilde {\operatorname {Kh}}(T)$ as Theorem 3.9 does for ![]() $\operatorname {HFT}(T)$.
$\operatorname {HFT}(T)$.
Theorem 5.13 Each component of the invariant ![]() $\widetilde {\operatorname {Kh}}(T)$ is either rational or special.
$\widetilde {\operatorname {Kh}}(T)$ is either rational or special.
The components of the invariant ![]() $\widetilde {\operatorname {BN}}(T)$ can be much more intricate than components of
$\widetilde {\operatorname {BN}}(T)$ can be much more intricate than components of ![]() $\widetilde {\operatorname {Kh}}(T)$, as the curve
$\widetilde {\operatorname {Kh}}(T)$, as the curve ![]() $\widetilde {\operatorname {BN}}(P_{2,-3})$ from Figure 13(d) illustrates. Even compact components can be more complicated, see for example [Reference Kotelskiy, Watson and ZibrowiusKWZ21b, Figure 15]. However, the proof of Theorem 5.13 still gives some restrictions for
$\widetilde {\operatorname {BN}}(P_{2,-3})$ from Figure 13(d) illustrates. Even compact components can be more complicated, see for example [Reference Kotelskiy, Watson and ZibrowiusKWZ21b, Figure 15]. However, the proof of Theorem 5.13 still gives some restrictions for ![]() $\widetilde {\operatorname {BN}}(T)$, too: For instance, the curve
$\widetilde {\operatorname {BN}}(T)$, too: For instance, the curve ![]() $\widetilde {\operatorname {BN}}(P_{2,-3})$ ‘wraps’ around the upper right tangle end, which is a non-special tangle end; in general, this kind of wrapping cannot occur around the special tangle end
$\widetilde {\operatorname {BN}}(P_{2,-3})$ ‘wraps’ around the upper right tangle end, which is a non-special tangle end; in general, this kind of wrapping cannot occur around the special tangle end ![]() $\ast$ (see [Reference Kotelskiy, Watson and ZibrowiusKWZ21b, Theorem 3.9]).
$\ast$ (see [Reference Kotelskiy, Watson and ZibrowiusKWZ21b, Theorem 3.9]).
6. Khovanov thin fillings
6.1 The  $\delta$-grading of curves in the covering space for
$\delta$-grading of curves in the covering space for  $\widetilde {\operatorname {Kh}}$ and
$\widetilde {\operatorname {Kh}}$ and  $\widetilde {\operatorname {BN}}$
$\widetilde {\operatorname {BN}}$
The parametrization of the four-punctured sphere that we use for the definition of the invariants ![]() $\widetilde {\operatorname {BN}}$ and
$\widetilde {\operatorname {BN}}$ and ![]() $\widetilde {\operatorname {Kh}}$ is different from the one used for
$\widetilde {\operatorname {Kh}}$ is different from the one used for ![]() $\operatorname {HFT}$: There are only two parametrizing arcs instead of four and one puncture is treated different from the other three. This also has consequences for how we think of the covering space
$\operatorname {HFT}$: There are only two parametrizing arcs instead of four and one puncture is treated different from the other three. This also has consequences for how we think of the covering space ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ of the four-punctured sphere. In this covering space, we think of the special puncture in terms of marked squares and of the non-special punctures as marked points. The arcs end at the vertices of the squares, as is drawn in Figure 13(d).
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ of the four-punctured sphere. In this covering space, we think of the special puncture in terms of marked squares and of the non-special punctures as marked points. The arcs end at the vertices of the squares, as is drawn in Figure 13(d).
To stay consistent with the conventions in [Reference Kotelskiy, Watson and ZibrowiusKWZ19], the normal vector field of all surfaces determined by the right-hand rule points out of the page. Thus, the boundary of a region of multiplicity 1 in the plane is oriented counter-clockwise. This is opposite to the conventions used in § 4; in particular, this results in the appearance of minus signs.
Lemma 6.1 For any connecting domain ![]() $\varphi$ from
$\varphi$ from ![]() $x$ to
$x$ to ![]() $x'$ (see Definition 4.3),
$x'$ (see Definition 4.3),
Lemma 6.2 With notation as in Definition 4.6, the ![]() $\delta$-grading of
$\delta$-grading of ![]() $\bullet$ is equal to
$\bullet$ is equal to
Proposition 6.3 For any tuple ![]() $(x_i)_{i=1,\ldots,n}$ of intersection points, a domain
$(x_i)_{i=1,\ldots,n}$ of intersection points, a domain ![]() $\varphi$ as in Definition 4.9 satisfies
$\varphi$ as in Definition 4.9 satisfies
 \[ \sum_{i=1}^n \delta(x_i)=2 e(\varphi)-\frac{n}{2}. \]
\[ \sum_{i=1}^n \delta(x_i)=2 e(\varphi)-\frac{n}{2}. \]
Corollary 6.4 For any domain ![]() $\varphi$ from
$\varphi$ from ![]() $x$ to
$x$ to ![]() $y$ (see Definition 4.11),
$y$ (see Definition 4.11),
Example 6.5 If ![]() $\varphi$ is a bigon of multiplicity 1 as in Figure 15, Corollary 6.4 implies that
$\varphi$ is a bigon of multiplicity 1 as in Figure 15, Corollary 6.4 implies that ![]() $\delta (y)-\delta (x)=-2e(\varphi )=-1$; see also [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Lemma 5.21].
$\delta (y)-\delta (x)=-2e(\varphi )=-1$; see also [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Lemma 5.21].

Figure 15. A bigon illustrating Example 6.5; compare with Figure 10 and [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Figure 17].
Proofs of results 6.1–6.4 The proofs of the two lemmas are very similar to those of Lemmas 4.5 and 4.7, respectively, since we were careful not to assume linearity of the curves in those proofs. Note that the square punctures can always be filled in if necessary, since they contribute 0 to the Euler measure.
For the first lemma, first consider the basic curve segments ![]() $\psi _i$,
$\psi _i$, ![]() $i=1,2,3,\ldots$, that are confined to a single face. In the case of an
$i=1,2,3,\ldots$, that are confined to a single face. In the case of an ![]() $S$-face, this is illustrated in Figure 16(a); for the
$S$-face, this is illustrated in Figure 16(a); for the ![]() $D$-faces, only the curve segments
$D$-faces, only the curve segments ![]() $\psi _i$ for even
$\psi _i$ for even ![]() $i$ are relevant. If
$i$ are relevant. If ![]() $\partial \tilde {\psi }_i=\tilde {x}'_i-\tilde {x}_i$, then for each integer
$\partial \tilde {\psi }_i=\tilde {x}'_i-\tilde {x}_i$, then for each integer ![]() $i$, there is a unique connecting domain
$i$, there is a unique connecting domain ![]() $\varphi _i$ from
$\varphi _i$ from ![]() $\tilde {x}_i$ to
$\tilde {x}_i$ to ![]() $\tilde {x}'_i$ avoiding the puncture of the face. The number of convex corners is equal to
$\tilde {x}'_i$ avoiding the puncture of the face. The number of convex corners is equal to ![]() $i+2$, so
$i+2$, so ![]() $e(\varphi _i)=\frac {1}{2}-{i}/{4}$. Moreover,
$e(\varphi _i)=\frac {1}{2}-{i}/{4}$. Moreover, ![]() $\psi _i$ corresponds to a component of the differential labeled by some algebra element
$\psi _i$ corresponds to a component of the differential labeled by some algebra element ![]() $a_i$, which is equal to
$a_i$, which is equal to ![]() $S^i$ for
$S^i$ for ![]() $S$-faces and equal to
$S$-faces and equal to ![]() $D^{i/2}$ for
$D^{i/2}$ for ![]() $D$-faces. Thus, in both cases
$D$-faces. Thus, in both cases ![]() $\delta (a_i)=-{i}/{2}$. Following the conventions from [Reference Kotelskiy, Watson and ZibrowiusKWZ19], the
$\delta (a_i)=-{i}/{2}$. Following the conventions from [Reference Kotelskiy, Watson and ZibrowiusKWZ19], the ![]() $\delta$-grading decreases along the differential by 1, so
$\delta$-grading decreases along the differential by 1, so
The argument for general domains is identical to that for ![]() $\operatorname {HFT}$.
$\operatorname {HFT}$.
Similarly, for Lemma 6.2, once we know the identity for regions confined to a single rectangle, the general case follows as in the proof of Lemma 4.7, using Lemma 6.1 in place of Lemma 4.5. Thus, let us consider those basic domains, which in the case of an ![]() $S$-face are illustrated in Figure 16(b). The differential corresponding to an intersection point can be easily read off by considering the two generators
$S$-face are illustrated in Figure 16(b). The differential corresponding to an intersection point can be easily read off by considering the two generators ![]() $\tilde {x}$ and
$\tilde {x}$ and ![]() $\tilde {y}$ on the first and second curve, respectively, that are connected by a path that turns right at the intersection point. The retraction of this path to the boundary of the face determines the label of the corresponding differential, namely
$\tilde {y}$ on the first and second curve, respectively, that are connected by a path that turns right at the intersection point. The retraction of this path to the boundary of the face determines the label of the corresponding differential, namely ![]() $S^i$ or
$S^i$ or ![]() $D^{i/2}$, where
$D^{i/2}$, where ![]() $i$ is the number of corners. Thus, the grading of the intersection point is
$i$ is the number of corners. Thus, the grading of the intersection point is
The connecting domain is a disc with ![]() $i+3$ convex corners and multiplicity
$i+3$ convex corners and multiplicity ![]() $+1$, so its Euler measure is equal to
$+1$, so its Euler measure is equal to ![]() $ ({1-i})/{4}$.
$ ({1-i})/{4}$.
Finally, the proofs of Proposition 6.3 and Corollary 6.4 are identical to the proofs of Proposition 4.10 and Corollary 4.12, respectively, except that we use Lemma 6.2 in place of Lemma 4.7.
6.2 Linear curves
Restricting to linear curves (Definition 4.14), we obtain results very similar to those in § 4.2.
Lemma 6.6 Let ![]() $\gamma$ be a linear curve of slope
$\gamma$ be a linear curve of slope ![]() $s\in \operatorname {\mathbb {Q}P}^1$. Then unless
$s\in \operatorname {\mathbb {Q}P}^1$. Then unless ![]() $s=0$, all intersection points with the horizontal lines of
$s=0$, all intersection points with the horizontal lines of ![]() $P$ have the same
$P$ have the same ![]() $\delta$-grading
$\delta$-grading ![]() $\delta _{-}:= \delta _{-}(\gamma )$, and unless
$\delta _{-}:= \delta _{-}(\gamma )$, and unless ![]() $s=\infty$, all intersection points with the vertical lines of
$s=\infty$, all intersection points with the vertical lines of ![]() $P$ have the same
$P$ have the same ![]() $\delta$-grading
$\delta$-grading ![]() $\delta _{|}:= \delta _{|}(\gamma )$. Moreover,
$\delta _{|}:= \delta _{|}(\gamma )$. Moreover,
 \[ \delta_{|}=\begin{cases} \delta_{-}-\frac{1}{2} & \text{if } 0< s<\infty ,\\ \delta_{-}+\frac{1}{2} & \text{if } \infty< s<0 . \end{cases} \]
\[ \delta_{|}=\begin{cases} \delta_{-}-\frac{1}{2} & \text{if } 0< s<\infty ,\\ \delta_{-}+\frac{1}{2} & \text{if } \infty< s<0 . \end{cases} \]
Lemma 6.7 Given two linear curves ![]() $\gamma$ and
$\gamma$ and ![]() $\gamma '$ of different slopes
$\gamma '$ of different slopes ![]() $s,s'\in \operatorname {\mathbb {Q}P}^1$, the Lagrangian intersection theory
$s,s'\in \operatorname {\mathbb {Q}P}^1$, the Lagrangian intersection theory ![]() $\operatorname {HF}(\gamma,\gamma ')$ is supported in a single
$\operatorname {HF}(\gamma,\gamma ')$ is supported in a single ![]() $\delta$-grading, which is equal to
$\delta$-grading, which is equal to
 \[ \delta(\gamma,\gamma') := \begin{cases} \delta_{-}(\gamma')-\delta_{|}(\gamma)-\tfrac{1}{2} & \text{if } s\in(\infty,s') \text{ for } s'\in(0,\infty], \text{ or } s\in(s',\infty) \text{ for } s'\in[\infty,0), \\ \delta_{|}(\gamma')-\delta_{-}(\gamma)-\tfrac{1}{2} & \text{if } s\in(s',0) \text{ for } s'\in[0,\infty), \text{ or } s\in(0,s') \text{ for } s'\in(\infty,0]. \end{cases} \]
\[ \delta(\gamma,\gamma') := \begin{cases} \delta_{-}(\gamma')-\delta_{|}(\gamma)-\tfrac{1}{2} & \text{if } s\in(\infty,s') \text{ for } s'\in(0,\infty], \text{ or } s\in(s',\infty) \text{ for } s'\in[\infty,0), \\ \delta_{|}(\gamma')-\delta_{-}(\gamma)-\tfrac{1}{2} & \text{if } s\in(s',0) \text{ for } s'\in[0,\infty), \text{ or } s\in(0,s') \text{ for } s'\in(\infty,0]. \end{cases} \]
Corollary 6.8 For any two linear curves ![]() $\gamma$ and
$\gamma$ and ![]() $\gamma '$,
$\gamma '$,
 \[ \delta(\gamma,\gamma')+\delta(\gamma',\gamma)= \begin{cases} 0 & \text{if } (\gamma)=s(\gamma'),\\ -1 & \text{if } s(\gamma)\neq s(\gamma'). \end{cases} \]
\[ \delta(\gamma,\gamma')+\delta(\gamma',\gamma)= \begin{cases} 0 & \text{if } (\gamma)=s(\gamma'),\\ -1 & \text{if } s(\gamma)\neq s(\gamma'). \end{cases} \]
Theorem 6.9 For any increasing triple ![]() $(\gamma,\gamma ',\gamma '')$ of linear curves,
$(\gamma,\gamma ',\gamma '')$ of linear curves,
Proof of results 6.6–6.9 The proof of Lemma 6.6 is identical to the proof of Lemma 4.15, except that the multiplicities of the triangles change sign and we use Lemma 6.1 in place of Lemma 4.5. Similarly, Lemma 6.7 follows from the same arguments as Lemma 4.17 using Lemma 6.2 in place of Lemma 4.7; note the opposite signs of the summands ![]() $\tfrac {1}{2}$. Corollary 6.8 follows immediately from Lemma 6.2, similar to Corollary 4.18. For Theorem 6.9, we can adapt the proof of Theorem 4.19 as follows. First, note that the triple
$\tfrac {1}{2}$. Corollary 6.8 follows immediately from Lemma 6.2, similar to Corollary 4.18. For Theorem 6.9, we can adapt the proof of Theorem 4.19 as follows. First, note that the triple ![]() $(\gamma '',\gamma ',\gamma )$ is decreasing, so let us swap the roles of
$(\gamma '',\gamma ',\gamma )$ is decreasing, so let us swap the roles of ![]() $\gamma ''$ and
$\gamma ''$ and ![]() $\gamma$ in the proof of Theorem 4.19. Then the domains
$\gamma$ in the proof of Theorem 4.19. Then the domains ![]() $\varphi$ and
$\varphi$ and ![]() $\varphi '$ only contain regions of multiplicity
$\varphi '$ only contain regions of multiplicity ![]() $-1$ and
$-1$ and ![]() $e(\Delta \tilde {A}\tilde {B}\tilde {C})=+\tfrac {1}{4}$. Using Lemma 6.2 in place of Lemma 4.7, this implies that
$e(\Delta \tilde {A}\tilde {B}\tilde {C})=+\tfrac {1}{4}$. Using Lemma 6.2 in place of Lemma 4.7, this implies that
 \begin{align*} \delta(\gamma'',\gamma')+\delta(\gamma',\gamma) &= (\delta(y)-\delta(x)-\tfrac{1}{2}+2e(\varphi))+ (\delta(z)-\delta(y)-\tfrac{1}{2}+2e(\varphi')) \\ &= \delta(z)-\delta(x)-\tfrac{3}{2}+2e(\varphi+\varphi'+\Delta\tilde{A}\tilde{B}\tilde{C}) = \delta(\gamma'',\gamma)-1. \end{align*}
\begin{align*} \delta(\gamma'',\gamma')+\delta(\gamma',\gamma) &= (\delta(y)-\delta(x)-\tfrac{1}{2}+2e(\varphi))+ (\delta(z)-\delta(y)-\tfrac{1}{2}+2e(\varphi')) \\ &= \delta(z)-\delta(x)-\tfrac{3}{2}+2e(\varphi+\varphi'+\Delta\tilde{A}\tilde{B}\tilde{C}) = \delta(\gamma'',\gamma)-1. \end{align*}
We add 2 on both sides, apply Corollary 6.8, multiply both sides by ![]() $-1$, and obtain
$-1$, and obtain
Lemma 6.10 Suppose ![]() $\gamma$ and
$\gamma$ and ![]() $\gamma '$ are two linear curves with local systems in
$\gamma '$ are two linear curves with local systems in ![]() $S^2_{4,\ast }$ that share the same slope
$S^2_{4,\ast }$ that share the same slope ![]() $s\in \operatorname {\mathbb {Q}P}^1$. Then, if
$s\in \operatorname {\mathbb {Q}P}^1$. Then, if ![]() $\gamma$ is rational and
$\gamma$ is rational and ![]() $\gamma '$ is special (or vice versa), the vector space
$\gamma '$ is special (or vice versa), the vector space ![]() $\operatorname {HF}(\gamma,\gamma ')$ is zero. Otherwise,
$\operatorname {HF}(\gamma,\gamma ')$ is zero. Otherwise, ![]() $\operatorname {HF}(\gamma,\gamma ')$ is non-zero and supported in two consecutive
$\operatorname {HF}(\gamma,\gamma ')$ is non-zero and supported in two consecutive ![]() $\delta$-gradings, namely
$\delta$-gradings, namely ![]() $\delta (\gamma,\gamma ')$ and
$\delta (\gamma,\gamma ')$ and ![]() $\delta (\gamma,\gamma ')-1$.
$\delta (\gamma,\gamma ')-1$.
Proof. Clearly, the Lagrangian Floer homology of a special and a rational curve vanishes. Moreover, any two curves of the same slope that are either both rational or both special intersect non-trivially, so ![]() $\operatorname {HF}(\gamma,\gamma ')$ does not vanish. The support of this vector space can be computed in the same way as in the proof of Lemma 4.20 for the case of two special curves.
$\operatorname {HF}(\gamma,\gamma ')$ does not vanish. The support of this vector space can be computed in the same way as in the proof of Lemma 4.20 for the case of two special curves.
Definition 6.11 In analogy to Definition 4.24, we say that a tangle ![]() $T$ is Khovanov exceptional if the multicurve
$T$ is Khovanov exceptional if the multicurve ![]() $\operatorname {Kh}(T)$ is exceptional.
$\operatorname {Kh}(T)$ is exceptional.
Conjecture 6.12 There exists no link ![]() $L$ for which
$L$ for which ![]() $\widetilde {\operatorname {Kh}}(L)$ is supported in precisely two non-adjacent
$\widetilde {\operatorname {Kh}}(L)$ is supported in precisely two non-adjacent ![]() $\delta$-gradings.
$\delta$-gradings.
Proposition 6.13 (Proposition 1.14)
If there exists a Khovanov exceptional tangle, then Conjecture 6.12 is false.
Proof. Suppose there exists a Khovanov exceptional tangle ![]() $T$. Let us write
$T$. Let us write ![]() $\Gamma =\widetilde {\operatorname {Kh}}(T)$ and
$\Gamma =\widetilde {\operatorname {Kh}}(T)$ and ![]() $\operatorname {\mathcal {S}}_{\Gamma }=\{s,s'\}$. By assumption,
$\operatorname {\mathcal {S}}_{\Gamma }=\{s,s'\}$. By assumption, ![]() $T$ is exceptional, so either
$T$ is exceptional, so either ![]() $|\delta (\gamma,\gamma ')|>1$ or
$|\delta (\gamma,\gamma ')|>1$ or ![]() $|\delta (\gamma ',\gamma )|>1$ for all components
$|\delta (\gamma ',\gamma )|>1$ for all components ![]() $\gamma,\gamma '\in \Gamma$ with
$\gamma,\gamma '\in \Gamma$ with ![]() $s(\gamma )=s$ and
$s(\gamma )=s$ and ![]() $s(\gamma ')=s'$. Without loss of generality, let us assume the former. Then, if we pick a slope
$s(\gamma ')=s'$. Without loss of generality, let us assume the former. Then, if we pick a slope ![]() $t\neq s$ such that
$t\neq s$ such that ![]() $(t,s,s')$ is increasing,
$(t,s,s')$ is increasing, ![]() $\delta (\mathbf {r}(t),\gamma ')=\delta (\mathbf {r}(t),\gamma )+\delta (\gamma,\gamma ')$ for all pairs
$\delta (\mathbf {r}(t),\gamma ')=\delta (\mathbf {r}(t),\gamma )+\delta (\gamma,\gamma ')$ for all pairs ![]() $(\gamma,\gamma ')$ as above. Since
$(\gamma,\gamma ')$ as above. Since ![]() $\Gamma$ is assumed to be
$\Gamma$ is assumed to be ![]() $s$- and
$s$- and ![]() $s'$-consistent,
$s'$-consistent, ![]() $\operatorname {HF}(\mathbf {r}(t),\Gamma )$ is supported in precisely two non-adjacent
$\operatorname {HF}(\mathbf {r}(t),\Gamma )$ is supported in precisely two non-adjacent ![]() $\delta$-gradings. Thus, by Theorem 5.8, the link
$\delta$-gradings. Thus, by Theorem 5.8, the link ![]() $Q_{-t}\cup T$ is a counterexample to Conjecture 6.12.
$Q_{-t}\cup T$ is a counterexample to Conjecture 6.12.
6.3 Khovanov thin fillings
In this subsection, ![]() $G$ is either
$G$ is either ![]() $\mathbb {Z}$ or
$\mathbb {Z}$ or ![]() $\mathbb {Z}/2$. Define
$\mathbb {Z}/2$. Define
In the following, we make implicit use of the following properties that ![]() $\operatorname {\mathfrak {C}_{\operatorname {Kh}}}$ is known to satisfy: each multicurve
$\operatorname {\mathfrak {C}_{\operatorname {Kh}}}$ is known to satisfy: each multicurve ![]() $\Gamma \in \operatorname {\mathfrak {C}_{\operatorname {Kh}}}$ consists of linear components only (Theorem 5.13); and
$\Gamma \in \operatorname {\mathfrak {C}_{\operatorname {Kh}}}$ consists of linear components only (Theorem 5.13); and ![]() $\operatorname {HF}(\Gamma _1,\Gamma _2)\neq 0$ for each
$\operatorname {HF}(\Gamma _1,\Gamma _2)\neq 0$ for each ![]() $\Gamma _1,\Gamma _2\in \operatorname {\mathfrak {C}_{\operatorname {Kh}}}$, because of Theorem 5.8 and the fact that reduced Khovanov homology does not vanish.
$\Gamma _1,\Gamma _2\in \operatorname {\mathfrak {C}_{\operatorname {Kh}}}$, because of Theorem 5.8 and the fact that reduced Khovanov homology does not vanish.
Given two multicurves ![]() $\Gamma$ and
$\Gamma$ and ![]() $\Gamma '$ and a slope
$\Gamma '$ and a slope ![]() $s\in \operatorname {\mathcal {S}}_\Gamma \cap \operatorname {\mathcal {S}}_{\Gamma '}$, the following condition will be relevant.
$s\in \operatorname {\mathcal {S}}_\Gamma \cap \operatorname {\mathcal {S}}_{\Gamma '}$, the following condition will be relevant.
Condition (R) At least one of
 $\Gamma$ and
$\Gamma$ and  $\Gamma '$ is
$\Gamma '$ is  $s$-rational, i.e. it only contains rational components of slope
$s$-rational, i.e. it only contains rational components of slope  $s$.
$s$.
This is the condition for reduced Khovanov theory mentioned in Theorems 1.12 and 1.15.
Definition 6.14 Given a relatively ![]() $\delta$-graded multicurve
$\delta$-graded multicurve ![]() $\Gamma$, let
$\Gamma$, let
be the spaces of ![]() $\boldsymbol {G}$-thin rational fillings of
$\boldsymbol {G}$-thin rational fillings of ![]() $\Gamma$. If
$\Gamma$. If ![]() $T$ is a Conway tangle in a three-ball, writing
$T$ is a Conway tangle in a three-ball, writing
recovers the definition from the introduction, which follows from Theorem 5.8.
Remark 6.15 Since by Lemma 5.9 the tangle invariant ![]() $\widetilde {\operatorname {Kh}}$ behaves in a natural way under mirroring,
$\widetilde {\operatorname {Kh}}$ behaves in a natural way under mirroring, ![]() $\Theta _{\mathrm {Kh}}(T^*)=\Theta ^{\operatorname {m}}_{\mathrm {Kh}}(T)$ and
$\Theta _{\mathrm {Kh}}(T^*)=\Theta ^{\operatorname {m}}_{\mathrm {Kh}}(T)$ and ![]() $\mathrm {A}_{\mathrm {Kh}}(T^*)=\mathrm {A}_{\mathrm {Kh}}^{\operatorname {m}}(T)$ for any Conway tangle
$\mathrm {A}_{\mathrm {Kh}}(T^*)=\mathrm {A}_{\mathrm {Kh}}^{\operatorname {m}}(T)$ for any Conway tangle ![]() $T$.
$T$.
The following result plays the same role for ![]() $\widetilde {\operatorname {Kh}}(T)$ as Theorem 4.27 does for
$\widetilde {\operatorname {Kh}}(T)$ as Theorem 4.27 does for ![]() $\operatorname {HFT}(T)$. Again, we denote the set of all line sets in the sense of § 2 by
$\operatorname {HFT}(T)$. Again, we denote the set of all line sets in the sense of § 2 by ![]() $\mathcal {P}_\mathrm {finite}(\operatorname {\mathfrak {C}})$.
$\mathcal {P}_\mathrm {finite}(\operatorname {\mathfrak {C}})$.
Theorem 6.16 There exist a map ![]() $\Phi \colon \thinspace \operatorname {\mathfrak {C}_{\operatorname {Kh}}}\rightarrow \mathcal {P}_\mathrm {finite}(\operatorname {\mathfrak {C}})$ and a map
$\Phi \colon \thinspace \operatorname {\mathfrak {C}_{\operatorname {Kh}}}\rightarrow \mathcal {P}_\mathrm {finite}(\operatorname {\mathfrak {C}})$ and a map ![]() $\operatorname {g}\colon \thinspace \operatorname {\mathfrak {C}}^2\rightarrow G$ satisfying (symmetry), (transitivity), and (linearity) properties as in § 2 such that for any
$\operatorname {g}\colon \thinspace \operatorname {\mathfrak {C}}^2\rightarrow G$ satisfying (symmetry), (transitivity), and (linearity) properties as in § 2 such that for any ![]() $\Gamma,\Gamma '\in \operatorname {\mathfrak {C}_{\operatorname {Kh}}}$, the following hold:
$\Gamma,\Gamma '\in \operatorname {\mathfrak {C}_{\operatorname {Kh}}}$, the following hold:
(i)
 $\operatorname {\mathcal {S}}_{\Gamma }=\operatorname {\mathcal {S}}_{\Phi (\Gamma )}$;
$\operatorname {\mathcal {S}}_{\Gamma }=\operatorname {\mathcal {S}}_{\Phi (\Gamma )}$;(ii)
 $\Theta _{\mathit {G}}(\Gamma )=\Theta _{\mathit {G}}(\Phi (\Gamma ))$;
$\Theta _{\mathit {G}}(\Gamma )=\Theta _{\mathit {G}}(\Phi (\Gamma ))$;(iii)
 $\Phi (\Gamma )$ is non-trivial;
$\Phi (\Gamma )$ is non-trivial;(iv)
 $\Phi (\Gamma )$ is exceptional if
$\Phi (\Gamma )$ is exceptional if  $\Gamma$ is exceptional;
$\Gamma$ is exceptional;(v) for any slope
 $s\in \operatorname {\mathbb {Q}P}^1$,
$s\in \operatorname {\mathbb {Q}P}^1$,  $\Gamma$ is
$\Gamma$ is  $s$-rational if and only if
$s$-rational if and only if  $\Phi (\Gamma )$ is
$\Phi (\Gamma )$ is  $s$-rational;
$s$-rational;(vi)
 $\operatorname {HF}(\Gamma,\Gamma ')$ is
$\operatorname {HF}(\Gamma,\Gamma ')$ is  $G$-thin if and only if the pair
$G$-thin if and only if the pair  $(\Phi (\Gamma ), \Phi (\Gamma '))$ is
$(\Phi (\Gamma ), \Phi (\Gamma '))$ is  $G$-thin.
$G$-thin.
Proof. Analogously to the proof of Theorem 4.27, given ![]() $c\in \operatorname {\mathfrak {C}}$, let
$c\in \operatorname {\mathfrak {C}}$, let ![]() $\gamma (c)$ be an absolutely
$\gamma (c)$ be an absolutely ![]() $\delta$-graded linear curve of slope
$\delta$-graded linear curve of slope ![]() $s(c)$ such that
$s(c)$ such that ![]() $\delta _{-}(\gamma (c))=\operatorname {g}(c)$ if
$\delta _{-}(\gamma (c))=\operatorname {g}(c)$ if ![]() $s(c)\neq 0$ and
$s(c)\neq 0$ and ![]() $\delta _{|}(\gamma (c))=\operatorname {g}(c)+\tfrac {1}{2}$ if
$\delta _{|}(\gamma (c))=\operatorname {g}(c)+\tfrac {1}{2}$ if ![]() $s(c)=0$. Then define
$s(c)=0$. Then define ![]() $\operatorname {g}\colon \thinspace \operatorname {\mathfrak {C}}^2\rightarrow G$ by setting for each
$\operatorname {g}\colon \thinspace \operatorname {\mathfrak {C}}^2\rightarrow G$ by setting for each ![]() $c,c' \in \operatorname {\mathfrak {C}}$
$c,c' \in \operatorname {\mathfrak {C}}$
By Corollary 6.8, (symmetry) of ![]() $\operatorname {g}$ holds, and by Theorem 6.9, so does (transitivity) of
$\operatorname {g}$ holds, and by Theorem 6.9, so does (transitivity) of ![]() $\operatorname {g}$. Moreover, (linearity) of
$\operatorname {g}$. Moreover, (linearity) of ![]() $\operatorname {g}$ follows from the definition.
$\operatorname {g}$ follows from the definition.
We can lift the ![]() $\delta$-grading of all curves in
$\delta$-grading of all curves in ![]() $\operatorname {\mathfrak {C}_{\operatorname {Kh}}}$ to an absolute
$\operatorname {\mathfrak {C}_{\operatorname {Kh}}}$ to an absolute ![]() $\delta$-grading such that for each component
$\delta$-grading such that for each component ![]() $\gamma$ of any element in
$\gamma$ of any element in ![]() $\operatorname {\mathfrak {C}_{\operatorname {Kh}}}$ we have
$\operatorname {\mathfrak {C}_{\operatorname {Kh}}}$ we have ![]() $\delta _{-}(\gamma )\in \mathbb {Z}, ~ \delta _{|}(\gamma )\in \mathbb {Z}+\tfrac 1 2$. To see that this is possible, we can apply the same arguments as in the proof of Theorem 4.27, now using Lemma 6.7 in place of Lemma 4.17 and the fact that reduced Khovanov homology is supported in integer
$\delta _{-}(\gamma )\in \mathbb {Z}, ~ \delta _{|}(\gamma )\in \mathbb {Z}+\tfrac 1 2$. To see that this is possible, we can apply the same arguments as in the proof of Theorem 4.27, now using Lemma 6.7 in place of Lemma 4.17 and the fact that reduced Khovanov homology is supported in integer ![]() $\delta$-gradings up to an overall shift, like knot Floer homology.
$\delta$-gradings up to an overall shift, like knot Floer homology.
Now, given some absolutely ![]() $\delta$-graded rational or special curve
$\delta$-graded rational or special curve ![]() $\gamma$ of slope
$\gamma$ of slope ![]() $s$, let
$s$, let ![]() $c=c(\gamma )\in \operatorname {\mathfrak {C}}$ be the line defined by
$c=c(\gamma )\in \operatorname {\mathfrak {C}}$ be the line defined by ![]() $s(c)=s$,
$s(c)=s$, ![]() $\varepsilon (c)=0$ if
$\varepsilon (c)=0$ if ![]() $\gamma$ is rational and 1 if
$\gamma$ is rational and 1 if ![]() $\gamma$ is special, and
$\gamma$ is special, and ![]() $\operatorname {g}(c)=\delta _{-}(\gamma )$ if
$\operatorname {g}(c)=\delta _{-}(\gamma )$ if ![]() $s\neq 0$ and
$s\neq 0$ and ![]() $\delta _{|}(\gamma )-\tfrac {1}{2}$ if
$\delta _{|}(\gamma )-\tfrac {1}{2}$ if ![]() $s(c)=0$. Then, given some
$s(c)=0$. Then, given some ![]() $\Gamma =\{\gamma _i\}_i\in \operatorname {\mathfrak {C}_{\operatorname {Kh}}}$, define
$\Gamma =\{\gamma _i\}_i\in \operatorname {\mathfrak {C}_{\operatorname {Kh}}}$, define ![]() $C(\Gamma )$ as the set corresponding to the multiset
$C(\Gamma )$ as the set corresponding to the multiset ![]() $\{c(\gamma _i)\}_{i}$.
$\{c(\gamma _i)\}_{i}$.
Properties (i)–(v) follow immediately from the definition of the map ![]() $\Phi$. The property (vi) follows from Lemmas 6.7 and 6.10.
$\Phi$. The property (vi) follows from Lemmas 6.7 and 6.10.
We can now show those parts of all theorems from the introduction concerning reduced Khovanov homology. Again, we are restating them here for clarity.
Theorem 6.17 (Characterization of Khovanov  $G$-thin filling spaces; Theorems 1.8 and 1.9)
$G$-thin filling spaces; Theorems 1.8 and 1.9)
For any Conway tangle ![]() $T$,
$T$, ![]() $\mathrm {A}_{\mathrm {Kh}}(T)$ is either empty, a single point or an interval in
$\mathrm {A}_{\mathrm {Kh}}(T)$ is either empty, a single point or an interval in ![]() $\operatorname {\mathbb {Q}P}^1$. Furthermore,
$\operatorname {\mathbb {Q}P}^1$. Furthermore, ![]() $\Theta _{\mathrm {Kh}}(T)$ is either empty, a single point, two distinct points or an interval in
$\Theta _{\mathrm {Kh}}(T)$ is either empty, a single point, two distinct points or an interval in ![]() $\operatorname {\mathbb {Q}P}^1$.
$\operatorname {\mathbb {Q}P}^1$.
Proposition 6.18 (Proposition 1.10)
If ![]() $\Theta _{\mathrm {Kh}}(T)$ is an interval,
$\Theta _{\mathrm {Kh}}(T)$ is an interval, ![]() $\Theta _{\mathrm {Kh}}(T)=\mathrm {A}_{\mathrm {Kh}}(T)$.
$\Theta _{\mathrm {Kh}}(T)=\mathrm {A}_{\mathrm {Kh}}(T)$.
In the following, let ![]() $T_1$ and
$T_1$ and ![]() $T_2$ be two Conway tangles and write
$T_2$ be two Conway tangles and write ![]() $\Gamma _1:= \operatorname {m}(\widetilde {\operatorname {Kh}}(T_1))$ and
$\Gamma _1:= \operatorname {m}(\widetilde {\operatorname {Kh}}(T_1))$ and ![]() $\Gamma _2:= \widetilde {\operatorname {Kh}}(T_2)$.
$\Gamma _2:= \widetilde {\operatorname {Kh}}(T_2)$.
Theorem 6.19 (A-link gluing theorem; Theorem 1.12)
Let ![]() $T_1$ and
$T_1$ and ![]() $T_2$ be two Conway tangles. Then
$T_2$ be two Conway tangles. Then ![]() $T_1\cup T_2$ is a Khovanov A-link if and only if:
$T_1\cup T_2$ is a Khovanov A-link if and only if:
(1)
 $\mathrm {A}_{\mathrm {Kh}}^{\operatorname {m}}(T_1) \cup \mathrm {A}_{\mathrm {Kh}}(T_2) = \operatorname {\mathbb {Q}P}^1$; and
$\mathrm {A}_{\mathrm {Kh}}^{\operatorname {m}}(T_1) \cup \mathrm {A}_{\mathrm {Kh}}(T_2) = \operatorname {\mathbb {Q}P}^1$; and(2) for every slope
 $s\in \partial \mathrm {A}_{\mathrm {Kh}}^{\operatorname {m}}(T_1) \cap \partial \mathrm {A}_{\mathrm {Kh}}(T_2)$, the multicurves
$s\in \partial \mathrm {A}_{\mathrm {Kh}}^{\operatorname {m}}(T_1) \cap \partial \mathrm {A}_{\mathrm {Kh}}(T_2)$, the multicurves  $\Gamma _1$ and
$\Gamma _1$ and  $\Gamma _2$ satisfy (R).
$\Gamma _2$ satisfy (R).
Proof of Theorem 6.19 By Theorem 5.8, ![]() $T_1\cup T_2$ is a A-link if and only if
$T_1\cup T_2$ is a A-link if and only if ![]() $\operatorname {HF}(\Gamma _1,\Gamma _2)$ is
$\operatorname {HF}(\Gamma _1,\Gamma _2)$ is ![]() $\mathbb {Z}/2$-thin. By Theorem 6.16(vi), the latter is equivalent to
$\mathbb {Z}/2$-thin. By Theorem 6.16(vi), the latter is equivalent to ![]() $(C_1,C_2)=\Phi (\Gamma _1,\Gamma _2)$ being
$(C_1,C_2)=\Phi (\Gamma _1,\Gamma _2)$ being ![]() $\mathbb {Z}/2$-thin. By Theorem 2.14, this is equivalent to
$\mathbb {Z}/2$-thin. By Theorem 2.14, this is equivalent to ![]() $\Theta _{\mathbb {Z}/2}(C_1)\cup \Theta _{\mathbb {Z}/2}(C_2)=\operatorname {\mathbb {Q}P}^1$ and for all
$\Theta _{\mathbb {Z}/2}(C_1)\cup \Theta _{\mathbb {Z}/2}(C_2)=\operatorname {\mathbb {Q}P}^1$ and for all ![]() $s\in \partial \mathrm {A}_{\mathrm {Kh}}^{\operatorname {m}}(T_1) \cap \partial \mathrm {A}_{\mathrm {Kh}}(T_2)$, at least one of
$s\in \partial \mathrm {A}_{\mathrm {Kh}}^{\operatorname {m}}(T_1) \cap \partial \mathrm {A}_{\mathrm {Kh}}(T_2)$, at least one of ![]() $C_1$ and
$C_1$ and ![]() $C_2$ is
$C_2$ is ![]() $s$-rational. By Theorem 6.16(v), the latter is equivalent to
$s$-rational. By Theorem 6.16(v), the latter is equivalent to ![]() $\Gamma _1$ and
$\Gamma _1$ and ![]() $\Gamma _2$ satisfying (R) for all
$\Gamma _2$ satisfying (R) for all ![]() $s\in \partial \mathrm {A}_{\mathrm {Kh}}^{\operatorname {m}}(T_1) \cap \partial \mathrm {A}_{\mathrm {Kh}}(T_2)$. Now use Theorem 6.16(ii) to conclude.
$s\in \partial \mathrm {A}_{\mathrm {Kh}}^{\operatorname {m}}(T_1) \cap \partial \mathrm {A}_{\mathrm {Kh}}(T_2)$. Now use Theorem 6.16(ii) to conclude.
Theorem 6.20 (Thin gluing theorem; Theorem 1.15)
Suppose ![]() $T_1$ and
$T_1$ and ![]() $T_2$ are two Conway tangle and at least one of them is not Khovanov exceptional. Then
$T_2$ are two Conway tangle and at least one of them is not Khovanov exceptional. Then ![]() $T_1\cup T_2$ is Khovanov thin if and only if:
$T_1\cup T_2$ is Khovanov thin if and only if:
(1)
 $\Theta ^{\operatorname {m}}_{\mathrm {Kh}}(T_1) \cup \Theta _{\mathrm {Kh}}(T_2) = \operatorname {\mathbb {Q}P}^1$; and
$\Theta ^{\operatorname {m}}_{\mathrm {Kh}}(T_1) \cup \Theta _{\mathrm {Kh}}(T_2) = \operatorname {\mathbb {Q}P}^1$; and(2) for every slope
 $s\in \partial \Theta^{{\rm m}}_{\mathrm {Kh}}(T_1) \cap \partial \Theta _{\mathrm {Kh}}(T_2)$, the multicurves
$s\in \partial \Theta^{{\rm m}}_{\mathrm {Kh}}(T_1) \cap \partial \Theta _{\mathrm {Kh}}(T_2)$, the multicurves  $\Gamma _1$ and
$\Gamma _1$ and  $\Gamma _2$ satisfy (R).
$\Gamma _2$ satisfy (R).
Proof. The proof is identical to that of Theorem 6.19, noting that the additional condition about exceptional multicurves is now needed when applying Theorem 2.14.
Unlike the Heegaard Floer setting, we do not know whether the exceptionality assumption in Theorem 4.31 is required, since Khovanov exceptional tangles have not been observed.
Corollary 6.21 (Corollaries 1.13 and 1.16)
For any Conway tangles ![]() $T_1$ and
$T_1$ and ![]() $T_2$,
$T_2$,
 \begin{gather*} \mathring{\mathrm{A}}_{\mathrm{Kh}}^{\operatorname{m}}(T_1) \cup \mathring{\mathrm{A}}_{\mathrm{Kh}}(T_2) = \operatorname{\mathbb{Q}P}^1 \Rightarrow L \text{ is a Khovanov A-link; and} \\ \mathring{\Theta}_{\mathrm{Kh}}^{\operatorname{m}}(T_1) \cup \mathring{\Theta}_{\mathrm{Kh}}(T_2) = \operatorname{\mathbb{Q}P}^1 \Rightarrow L \text{ is Khovanov thin.} \end{gather*}
\begin{gather*} \mathring{\mathrm{A}}_{\mathrm{Kh}}^{\operatorname{m}}(T_1) \cup \mathring{\mathrm{A}}_{\mathrm{Kh}}(T_2) = \operatorname{\mathbb{Q}P}^1 \Rightarrow L \text{ is a Khovanov A-link; and} \\ \mathring{\Theta}_{\mathrm{Kh}}^{\operatorname{m}}(T_1) \cup \mathring{\Theta}_{\mathrm{Kh}}(T_2) = \operatorname{\mathbb{Q}P}^1 \Rightarrow L \text{ is Khovanov thin.} \end{gather*}
Proof. Let ![]() $C_i=\Phi (\Gamma _i)$ for
$C_i=\Phi (\Gamma _i)$ for ![]() $i=1,2$. By Theorem 6.16(ii),
$i=1,2$. By Theorem 6.16(ii), ![]() $\mathring {\mathrm {A}}_{\mathrm {Kh}}^{\operatorname {m}}(T_1) \cup \mathring {\mathrm {A}}_{\mathrm {Kh}}(T_2) = \operatorname {\mathbb {Q}P}^1$ implies that
$\mathring {\mathrm {A}}_{\mathrm {Kh}}^{\operatorname {m}}(T_1) \cup \mathring {\mathrm {A}}_{\mathrm {Kh}}(T_2) = \operatorname {\mathbb {Q}P}^1$ implies that ![]() $\mathring {\Theta }_{\mathbb {Z}/2}(C_1)\cup \mathring {\Theta }_{\mathbb {Z}/2}(C_2)=\operatorname {\mathbb {Q}P}^1$. By Corollary 2.16,
$\mathring {\Theta }_{\mathbb {Z}/2}(C_1)\cup \mathring {\Theta }_{\mathbb {Z}/2}(C_2)=\operatorname {\mathbb {Q}P}^1$. By Corollary 2.16, ![]() $(C_1,C_2)$ is
$(C_1,C_2)$ is ![]() $\mathbb {Z}/2$-thin, so by Theorem 6.16(vi), this implies that
$\mathbb {Z}/2$-thin, so by Theorem 6.16(vi), this implies that ![]() $\operatorname {HF}(\Gamma _1,\Gamma _2)$ is
$\operatorname {HF}(\Gamma _1,\Gamma _2)$ is ![]() $\mathbb {Z}/2$-thin. Now conclude with Theorem 5.8.
$\mathbb {Z}/2$-thin. Now conclude with Theorem 5.8.
The second part follows from the same line of reasoning.
7. Examples
In order to place the theorems in this paper in context, we conclude with a collection of examples. Of note is the fact that the behaviour one encounters in practice is relatively tame, by comparison with the delicate casework seen in the proofs. In particular, if one chooses to focus on the invariants that are encountered in nature, for instance in the examples computed in [Reference Kotelskiy, Watson and ZibrowiusKWZ22], most of the forgoing material simplifies considerably. We attempt to highlight this here, and with the reader who has skipped directly to this section from the introduction in mind, our aim is to present this material in a vaguely self-contained way.
For simplicity, we focus on Khovanov homology throughout this section; the analogous statements hold for link Floer homology as well. In fact, for many examples, the notions of thinness are independent of the homology theory and the field of coefficients. Using the programs [Reference Greene and MorrisonGM20] and [Reference SzabóSza20], we checked that through 14-crossing knots the invariants ![]() $\widetilde {\operatorname {Kh}}(K;{\mathbb {F}}_2)$,
$\widetilde {\operatorname {Kh}}(K;{\mathbb {F}}_2)$, ![]() $\widetilde {\operatorname {Kh}}(K;\mathbb {Q})$,
$\widetilde {\operatorname {Kh}}(K;\mathbb {Q})$, ![]() $\operatorname {\widehat {HFK}}(K;{\mathbb {F}}_2)$, and
$\operatorname {\widehat {HFK}}(K;{\mathbb {F}}_2)$, and ![]() $\operatorname {\widehat {HFK}}(K;{\mathbb {F}}_3)$ are either simultaneously thin or simultaneously not thin. However, Shumakovitch gave the following cautionary example [Reference ShumakovitchShu21]; we thank Lukas Lewark for pointing it out to us.
$\operatorname {\widehat {HFK}}(K;{\mathbb {F}}_3)$ are either simultaneously thin or simultaneously not thin. However, Shumakovitch gave the following cautionary example [Reference ShumakovitchShu21]; we thank Lukas Lewark for pointing it out to us.
Example 7.1 The Khovanov homology of the knot ![]() $16^n_{197566}$ in the knotscape knot table [Reference Hoste and ThistlethwaiteHT21] is thin when computed with rational coefficients, but not over
$16^n_{197566}$ in the knotscape knot table [Reference Hoste and ThistlethwaiteHT21] is thin when computed with rational coefficients, but not over ![]() ${\mathbb {F}}_2$. Shumakovitch used unreduced Khovanov homology, but this statement is also true for reduced Khovanov homology; see the example K_16n197566 in [Reference Kotelskiy, Watson and ZibrowiusKWZ21a]. Interestingly, knot Floer homology is thin over
${\mathbb {F}}_2$. Shumakovitch used unreduced Khovanov homology, but this statement is also true for reduced Khovanov homology; see the example K_16n197566 in [Reference Kotelskiy, Watson and ZibrowiusKWZ21a]. Interestingly, knot Floer homology is thin over ![]() ${\mathbb {F}}$; we checked this using Szabó's program [Reference SzabóSza20]. We expand on these calculations in Example 7.14.
${\mathbb {F}}$; we checked this using Szabó's program [Reference SzabóSza20]. We expand on these calculations in Example 7.14.
Despite this example, the following question remains open.
Question 7.2 Does the notion of thinness agree for Khovanov and Heegaard Floer theories when working with coefficients in ![]() $\mathbb {Q}$?
$\mathbb {Q}$?
It is convenient to describe the Khovanov invariants of tangles in the planar cover ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ of the tangle boundary minus the tangle endpoints. One reason for this is the somewhat surprising fact, stated in Theorem 5.13, that for any Conway tangle
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ of the tangle boundary minus the tangle endpoints. One reason for this is the somewhat surprising fact, stated in Theorem 5.13, that for any Conway tangle ![]() $T$, all of the components are linear. This is illustrated in Figure 17, which revisits Example 5.4. This particular
$T$, all of the components are linear. This is illustrated in Figure 17, which revisits Example 5.4. This particular ![]() $(2,-3)$-pretzel tangle serves as a running example through this section. Note that Theorem 5.2 says that
$(2,-3)$-pretzel tangle serves as a running example through this section. Note that Theorem 5.2 says that ![]() $\widetilde {\operatorname {Kh}}$ commutes with the action of the mapping class group; this group is generated by a pair of plane shears on
$\widetilde {\operatorname {Kh}}$ commutes with the action of the mapping class group; this group is generated by a pair of plane shears on ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$. As a result, the bottom braid move relating the pretzel tangles
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$. As a result, the bottom braid move relating the pretzel tangles ![]() $P_{2,-3}$ and
$P_{2,-3}$ and ![]() $P_{-2,-3}$ lifts to a linear transformation of the planar cover. For the class of tangles admitting an unknot closure, there is a sense in which the behaviour one sees is not more complicated than that observed in this single example; see [Reference Kotelskiy, Watson and ZibrowiusKWZ22] for more. This is an ungraded statement, however: the grading information is subtle and important.
$P_{-2,-3}$ lifts to a linear transformation of the planar cover. For the class of tangles admitting an unknot closure, there is a sense in which the behaviour one sees is not more complicated than that observed in this single example; see [Reference Kotelskiy, Watson and ZibrowiusKWZ22] for more. This is an ungraded statement, however: the grading information is subtle and important.

Figure 17. The Khovanov invariant of a tangle as curves lifted to the cover ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$. Note that the tangles
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$. Note that the tangles ![]() $P_{2,-3}$ and
$P_{2,-3}$ and ![]() $P_{-2,-3}$ are related by adding a half-twist at the lower endpoints and a flype; this is reflected in the plane shear taking one invariant to the other. As expected, both special and rational components (in the sense of Definition 5.11) appear.
$P_{-2,-3}$ are related by adding a half-twist at the lower endpoints and a flype; this is reflected in the plane shear taking one invariant to the other. As expected, both special and rational components (in the sense of Definition 5.11) appear.
7.1 Rational tangles and two-bridge knots: conventions
We begin by providing a cheat sheet of sorts in order to fix our conventions. The left-hand trefoil, expressed as the closure of the three-crossing rational tangle ![]() $Q_3$ by the trivial tangle
$Q_3$ by the trivial tangle ![]() $Q_0$, is shown in Figure 18. With this example we mean to highlight that there is a strong interplay between the Khovanov and Bar-Natan invariants of a given tangle.
$Q_0$, is shown in Figure 18. With this example we mean to highlight that there is a strong interplay between the Khovanov and Bar-Natan invariants of a given tangle.

Figure 18. A decomposition of the trefoil knot into the three-crossing rational tangle ![]() $Q_3$ and the trivial tangle
$Q_3$ and the trivial tangle ![]() $Q_0$ (top right) and the corresponding computation of the reduced Khovanov homology of the trefoil knot in terms of Lagrangian Floer homology in the covering space (left):
$Q_0$ (top right) and the corresponding computation of the reduced Khovanov homology of the trefoil knot in terms of Lagrangian Floer homology in the covering space (left): ![]() $\widetilde {\operatorname {Kh}}(Q_0\cup Q_3)\otimes V \cong \operatorname {HF}(\widetilde {\operatorname {Kh}}(Q_0^*),\widetilde {\operatorname {Kh}}(Q_3)) = {\mathbb {F}}^6$ and
$\widetilde {\operatorname {Kh}}(Q_0\cup Q_3)\otimes V \cong \operatorname {HF}(\widetilde {\operatorname {Kh}}(Q_0^*),\widetilde {\operatorname {Kh}}(Q_3)) = {\mathbb {F}}^6$ and ![]() $\widetilde {\operatorname {Kh}}(Q_0^* \cup Q_3) \cong \operatorname {HF}(\widetilde {\operatorname {Kh}}(Q_0^*),\widetilde {\operatorname {BN}}(Q_3)) ={\mathbb {F}}^3$. A shorthand for this calculation is depicted on the bottom-right.
$\widetilde {\operatorname {Kh}}(Q_0^* \cup Q_3) \cong \operatorname {HF}(\widetilde {\operatorname {Kh}}(Q_0^*),\widetilde {\operatorname {BN}}(Q_3)) ={\mathbb {F}}^3$. A shorthand for this calculation is depicted on the bottom-right.
Indeed, although we have been working almost exclusively with ![]() $\widetilde {\operatorname {Kh}}(T_1\cup T_2)\otimes V$ to this point (see § 5.2), recall that
$\widetilde {\operatorname {Kh}}(T_1\cup T_2)\otimes V$ to this point (see § 5.2), recall that ![]() $\widetilde {\operatorname {Kh}}(T_1\cup T_2)$ can also be recovered by considering
$\widetilde {\operatorname {Kh}}(T_1\cup T_2)$ can also be recovered by considering ![]() $\operatorname {HF}(\widetilde {\operatorname {Kh}}(T_1^*),\widetilde {\operatorname {BN}}(T_2))$. To compute the Floer homology in the planar cover, it is sufficient to consider the preimage of one multicurve, the lift of the other multicurve, and then count intersections after pulling tight. This strategy is used on the left of Figure 18: the preimage of
$\operatorname {HF}(\widetilde {\operatorname {Kh}}(T_1^*),\widetilde {\operatorname {BN}}(T_2))$. To compute the Floer homology in the planar cover, it is sufficient to consider the preimage of one multicurve, the lift of the other multicurve, and then count intersections after pulling tight. This strategy is used on the left of Figure 18: the preimage of ![]() $\widetilde {\operatorname {Kh}}(Q_0)$ are the lines of slope
$\widetilde {\operatorname {Kh}}(Q_0)$ are the lines of slope ![]() $0$, and the lift of the invariant
$0$, and the lift of the invariant ![]() $\widetilde {\operatorname {Kh}}(Q_3)$ is the line of slope
$\widetilde {\operatorname {Kh}}(Q_3)$ is the line of slope ![]() $3$ missing the punctures, twice longer than the other line of slope 3 shown. The latter line, which passes through punctures, coincides with the lift of the Bar-Natan invariant
$3$ missing the punctures, twice longer than the other line of slope 3 shown. The latter line, which passes through punctures, coincides with the lift of the Bar-Natan invariant ![]() $\widetilde {\operatorname {BN}}(Q_3)$. The fact that the trefoil is thin is well known; through the lens of our results, this is the fact that a line of slope 3 in the plane intersects a line of slope 0 once.
$\widetilde {\operatorname {BN}}(Q_3)$. The fact that the trefoil is thin is well known; through the lens of our results, this is the fact that a line of slope 3 in the plane intersects a line of slope 0 once.
More generally, a central observation in this work is that the invariant of a rational tangle corresponds to/is controlled by a line of the appropriate rational slope. Although this has come up repeatedly already, we review this basic fact here in order to make some conventions concrete and transparent; see Figure 19. Rational fillings of the trivial tangle ![]() $Q_0$ are non-split two-bridge links, with the exception of the slope 0 rational filling, which is the two-component unlink. This unlink is not an A-link. However, non-split two-bridge links are alternating and, hence, thin by [Reference LeeLee05, Theorem 3.12], see also [Reference Manolescu and OzsváthMO08, Theorem 1]. Thus, we know that
$Q_0$ are non-split two-bridge links, with the exception of the slope 0 rational filling, which is the two-component unlink. This unlink is not an A-link. However, non-split two-bridge links are alternating and, hence, thin by [Reference LeeLee05, Theorem 3.12], see also [Reference Manolescu and OzsváthMO08, Theorem 1]. Thus, we know that ![]() $\Theta (Q_0)=\mathrm {A}(Q_0)=\operatorname {\mathbb {Q}P}^1\smallsetminus \{0\}$.
$\Theta (Q_0)=\mathrm {A}(Q_0)=\operatorname {\mathbb {Q}P}^1\smallsetminus \{0\}$.

Figure 19. Some closures of rational tangles associated with odd-length positive continued fractions, together with their Khovanov homology groups calculated via intersection in the plane according to the shorthand explained in Figure 18. Note that ![]() $[3]={3}/{1}$ is the left-hand trefoil whereas
$[3]={3}/{1}$ is the left-hand trefoil whereas ![]() $[1,1,1]={3}/{2}$ is the right-hand trefoil. We recover the Khovanov homology for the Hopf link (dimension 2), both trefoils (dimension 3), and the figure-eight knot (dimension 5). In general, the alternating three-braid
$[1,1,1]={3}/{2}$ is the right-hand trefoil. We recover the Khovanov homology for the Hopf link (dimension 2), both trefoils (dimension 3), and the figure-eight knot (dimension 5). In general, the alternating three-braid ![]() $\beta =\sigma _2^{-a_0}\sigma _1^{a_1}\sigma _2^{-a_2}\sigma _1^{a_3}\cdots \sigma _2^{-a_n}$, inserted into the tangle as indicated on the right, gives rise to the two-bridge link associated with the odd-length continued fraction
$\beta =\sigma _2^{-a_0}\sigma _1^{a_1}\sigma _2^{-a_2}\sigma _1^{a_3}\cdots \sigma _2^{-a_n}$, inserted into the tangle as indicated on the right, gives rise to the two-bridge link associated with the odd-length continued fraction ![]() $[a_0,a_1,\ldots,a_{n}]$.
$[a_0,a_1,\ldots,a_{n}]$.
We now consider this in more detail, making the choice to vary the rational tangle and to fix the particular closure: the numerator closure ![]() $Q_0$ as in Figure 19. Given a positive, reduced rational number
$Q_0$ as in Figure 19. Given a positive, reduced rational number ![]() ${p}/{q}\ge 1$, there is a unique non-split two-bridge link associated with it. To construct it, one chooses an odd-length positive continued fraction expansion
${p}/{q}\ge 1$, there is a unique non-split two-bridge link associated with it. To construct it, one chooses an odd-length positive continued fraction expansion
 \[ {p}/{q} = [a_0,a_1,\ldots,a_n] = a_n+\cfrac{1}{a_{n-1}+\cfrac{1}{\cdots+\cfrac{1}{a_0}}}, \]
\[ {p}/{q} = [a_0,a_1,\ldots,a_n] = a_n+\cfrac{1}{a_{n-1}+\cfrac{1}{\cdots+\cfrac{1}{a_0}}}, \]
where ![]() $a_i>0$ and
$a_i>0$ and ![]() $n>0$ is even. Since
$n>0$ is even. Since ![]() $[a_0,\ldots,a_{n}] = [1,a_0-1,\ldots,a_{n}]$ for
$[a_0,\ldots,a_{n}] = [1,a_0-1,\ldots,a_{n}]$ for ![]() $a_0\neq 1$, such a continued fraction expansion always exists. With this choice in hand, Figure 19 illustrates some examples of two-bridge knots obtained as the numerator closures of rational tangles. Each rational number is associated with a slope in the plane, and the intersection of the corresponding line with the preimage of
$a_0\neq 1$, such a continued fraction expansion always exists. With this choice in hand, Figure 19 illustrates some examples of two-bridge knots obtained as the numerator closures of rational tangles. Each rational number is associated with a slope in the plane, and the intersection of the corresponding line with the preimage of ![]() $\widetilde {\operatorname {Kh}}(Q_0)$ in the plane calculates the Khovanov homology of the associated two-bridge knot. We have shown the slopes
$\widetilde {\operatorname {Kh}}(Q_0)$ in the plane calculates the Khovanov homology of the associated two-bridge knot. We have shown the slopes ![]() ${3}/{2}<2<{5}/{2}<3$ in the plane to illustrate these thin fillings. The fact that the numerator
${3}/{2}<2<{5}/{2}<3$ in the plane to illustrate these thin fillings. The fact that the numerator ![]() $p$ calculates the determinant and the dimension of the reduced Khovanov homology is a helpful check for these examples. It can be instructive to consider the base-length 1 parallelograms determined by the Khovanov invariants in each case; the added twists dictated by the continued fraction correspond in a natural way to the plane shears moving between any two parallelograms. Moreover, with the above conventions in place, the area of the parallelogram agrees with the determinant of the link.
$p$ calculates the determinant and the dimension of the reduced Khovanov homology is a helpful check for these examples. It can be instructive to consider the base-length 1 parallelograms determined by the Khovanov invariants in each case; the added twists dictated by the continued fraction correspond in a natural way to the plane shears moving between any two parallelograms. Moreover, with the above conventions in place, the area of the parallelogram agrees with the determinant of the link.
7.2 An aside on alternating fillings
In these first examples, thinness was deduced from the stronger statement that all tangle fillings in question were alternating. In general, we can say a little more. For terminology, we say a tangle diagram is alternating if the crossings alternate between under and over crossings as one travels along the tangle, regardless of where one starts. We call a tangle diagram connected if the underlying planar graph is connected.
Proposition 7.3 For any tangle ![]() $T$ admitting a connected alternating diagram, the space of thin fillings (relative to a choice of alternating tangle diagram) contains either
$T$ admitting a connected alternating diagram, the space of thin fillings (relative to a choice of alternating tangle diagram) contains either ![]() $[\infty,0]$ or
$[\infty,0]$ or ![]() $[0,\infty ]$. Moreover, these thin fillings are in fact alternating fillings.
$[0,\infty ]$. Moreover, these thin fillings are in fact alternating fillings.
It is interesting to compare Proposition 7.3 to a result of Bar-Natan and Burgos-Soto [Reference Bar-Natan and Burgos-SotoBNBS14, Theorem 1]. When restricted to Conway tangles, their result says that the vertical (horizontal) intersection points of ![]() $\widetilde {\operatorname {Kh}}(T)$ have the same
$\widetilde {\operatorname {Kh}}(T)$ have the same ![]() $\delta$-grading
$\delta$-grading ![]() $\delta _{|}$ (
$\delta _{|}$ (![]() $\delta _{-}$), and that
$\delta _{-}$), and that ![]() $\delta _{|}$ and
$\delta _{|}$ and ![]() $\delta _{-}$ differ by
$\delta _{-}$ differ by ![]() $\pm \tfrac {1}{2}$. The fact that both
$\pm \tfrac {1}{2}$. The fact that both ![]() $\delta _{|}$ and
$\delta _{|}$ and ![]() $\delta _{-}$ are constant implies that
$\delta _{-}$ are constant implies that ![]() $\widetilde {\operatorname {Kh}}(T)$ neither contains any special component of slope
$\widetilde {\operatorname {Kh}}(T)$ neither contains any special component of slope ![]() $0$ nor any special component of slope
$0$ nor any special component of slope ![]() $\infty$. Indeed, observe that special components of slope
$\infty$. Indeed, observe that special components of slope ![]() $0$ contain two pairs of generators whose
$0$ contain two pairs of generators whose ![]() $\delta$-gradings are equal to
$\delta$-gradings are equal to ![]() $\delta _{|}-\tfrac {1}{2}$ and
$\delta _{|}-\tfrac {1}{2}$ and ![]() $\delta _{|}+\tfrac {1}{2}$, respectively. Similarly, any special component of slope
$\delta _{|}+\tfrac {1}{2}$, respectively. Similarly, any special component of slope ![]() $\infty$ contains four generators whose
$\infty$ contains four generators whose ![]() $\delta$-gradings are equal to
$\delta$-gradings are equal to ![]() $\delta _{-}-\tfrac {1}{2}$ and
$\delta _{-}-\tfrac {1}{2}$ and ![]() $\delta _{-}+\tfrac {1}{2}$. In fact,
$\delta _{-}+\tfrac {1}{2}$. In fact, ![]() $\widetilde {\operatorname {Kh}}(T)$ does not contain any rational component of slope
$\widetilde {\operatorname {Kh}}(T)$ does not contain any rational component of slope ![]() $0$ or
$0$ or ![]() $\infty$ either, since
$\infty$ either, since ![]() $0,\infty \in \Theta _{\mathrm {Kh}}(T)$. This implies the following strengthening of Proposition 7.3:
$0,\infty \in \Theta _{\mathrm {Kh}}(T)$. This implies the following strengthening of Proposition 7.3:
Corollary 7.4 For any tangle ![]() $T$ admitting a connected alternating diagram,
$T$ admitting a connected alternating diagram, ![]() $\Theta _{\mathrm {Kh}}(T)$ contains an open interval containing both
$\Theta _{\mathrm {Kh}}(T)$ contains an open interval containing both ![]() $\infty$ and
$\infty$ and ![]() $0$.
$0$.
For ![]() $\operatorname {HFT}$, a similar result seems plausible. In fact, the corresponding statement about the horizontal and vertical
$\operatorname {HFT}$, a similar result seems plausible. In fact, the corresponding statement about the horizontal and vertical ![]() $\delta$-grading also holds for
$\delta$-grading also holds for ![]() $\operatorname {HFT}(T)$, which follows from the generalised clock theorem [Reference ZibrowiusZib15]. However,
$\operatorname {HFT}(T)$, which follows from the generalised clock theorem [Reference ZibrowiusZib15]. However, ![]() $\operatorname {HFT}$ may contain rational components of slope
$\operatorname {HFT}$ may contain rational components of slope ![]() $0$ or
$0$ or ![]() $\infty$ that carry inhibited local systems, see Definition 4.21 and Remark 4.23.
$\infty$ that carry inhibited local systems, see Definition 4.21 and Remark 4.23.
Proof of Proposition 7.3 Consider a connected alternating diagram ![]() $D$ of the tangle
$D$ of the tangle ![]() $T$. The two closures of
$T$. The two closures of ![]() $D$ representing the links
$D$ representing the links ![]() $T(0)$ and
$T(0)$ and ![]() $T(\infty )$ are alternating diagrams and, since they are non-split, the links
$T(\infty )$ are alternating diagrams and, since they are non-split, the links ![]() $T(0)$ and
$T(0)$ and ![]() $T(\infty )$ are non-split [Reference LickorishLic97, Theorem 4.2]. Similarly, either the
$T(\infty )$ are non-split [Reference LickorishLic97, Theorem 4.2]. Similarly, either the ![]() $+1$- or
$+1$- or ![]() $-1$-closure of
$-1$-closure of ![]() $D$ is an alternating diagram, so at least one of
$D$ is an alternating diagram, so at least one of ![]() $T(+1)$ and
$T(+1)$ and ![]() $T(-1)$ is an alternating non-split link. Any alternating non-split link has thin Khovanov homology. So
$T(-1)$ is an alternating non-split link. Any alternating non-split link has thin Khovanov homology. So ![]() $\Theta (T)$ contains
$\Theta (T)$ contains ![]() $0$,
$0$, ![]() $\infty$ and either
$\infty$ and either ![]() $+1$ or
$+1$ or ![]() $-1$. By Theorem 1.9, it is therefore an interval containing either
$-1$. By Theorem 1.9, it is therefore an interval containing either ![]() $[0,\infty ]$ or
$[0,\infty ]$ or ![]() $[\infty,0]$.
$[\infty,0]$.
One can now check directly that ![]() $T(s)$ is alternating either for all positive or for all negative
$T(s)$ is alternating either for all positive or for all negative ![]() $s\in \operatorname {\mathbb {Q}P}^1$. Indeed, without loss of generality, suppose that
$s\in \operatorname {\mathbb {Q}P}^1$. Indeed, without loss of generality, suppose that ![]() $T(+1)$ is alternating. Then according to our conventions
$T(+1)$ is alternating. Then according to our conventions ![]() $T(n)$ is an alternating diagram for all
$T(n)$ is an alternating diagram for all ![]() $n\ge 0$. More generally, we simply observe that choosing an odd-length continued fraction representing a positive rational number
$n\ge 0$. More generally, we simply observe that choosing an odd-length continued fraction representing a positive rational number ![]() $s$ (compare Figure 19), the closure
$s$ (compare Figure 19), the closure ![]() $T(s)$ is an alternating diagram.
$T(s)$ is an alternating diagram.
One can easily check the proposition on the class of two-bridge links, for example, by starting from a rational tangle diagram with one crossing.
7.3 A more instructive example
Perhaps the simplest non-rational tangle without closed components is the ![]() $(2,-3)$-pretzel tangle
$(2,-3)$-pretzel tangle ![]() $P_{2,-3}$. The Khovanov invariant associated with this tangle is given in Figure 17 and revisited in Figure 20. It consists of a special component (the curve of slope
$P_{2,-3}$. The Khovanov invariant associated with this tangle is given in Figure 17 and revisited in Figure 20. It consists of a special component (the curve of slope ![]() $\infty$) and a rational component (the curve of slope
$\infty$) and a rational component (the curve of slope ![]() $-2$).
$-2$).

Figure 20. The invariant for ![]() $P_{2,-3}$ illustrating that
$P_{2,-3}$ illustrating that ![]() $\Theta _{\mathrm {Kh}}(P_{2,-3})= \mathrm {A}_{\mathrm {Kh}}(P_{2,-3})=(-2,\infty ]$. The fillings
$\Theta _{\mathrm {Kh}}(P_{2,-3})= \mathrm {A}_{\mathrm {Kh}}(P_{2,-3})=(-2,\infty ]$. The fillings ![]() $-1$,
$-1$, ![]() $0$, and
$0$, and ![]() $+1$ have been indicated, each of which is an alternating link. Note that, after an appropriate isotopy fixing the tangle boundary setwise on each of the links in the shaded boxes, the closures we have identified are realized as closures of alternating tangles. As a result,
$+1$ have been indicated, each of which is an alternating link. Note that, after an appropriate isotopy fixing the tangle boundary setwise on each of the links in the shaded boxes, the closures we have identified are realized as closures of alternating tangles. As a result, ![]() $[-1,1]\subset (-2,\infty ]$ gives a subset of alternating fillings according to Proposition 7.3.
$[-1,1]\subset (-2,\infty ]$ gives a subset of alternating fillings according to Proposition 7.3.
To compute the spaces of thin and A-link fillings of this tangle, observe that the 0-rational filling ![]() $P_{2,-3}(0)$ is a connected sum of the trefoil knot and the Hopf link. Thus, this filling is thin and an A-link. (Alternatively, this follows from the fact that the horizontal
$P_{2,-3}(0)$ is a connected sum of the trefoil knot and the Hopf link. Thus, this filling is thin and an A-link. (Alternatively, this follows from the fact that the horizontal ![]() $\delta$-gradings
$\delta$-gradings ![]() $\delta _{-}$ of the two components of
$\delta _{-}$ of the two components of ![]() $\widetilde {\operatorname {Kh}}(P_{2,-3})$ agree; see Table 1.) Having found one thin filling whose slope does not agree with one of the supporting slopes of
$\widetilde {\operatorname {Kh}}(P_{2,-3})$ agree; see Table 1.) Having found one thin filling whose slope does not agree with one of the supporting slopes of ![]() $\widetilde {\operatorname {Kh}}(P_{2,-3})$, we now know that
$\widetilde {\operatorname {Kh}}(P_{2,-3})$, we now know that ![]() $\Theta _{\mathrm {Kh}}(P_{2,-3})$ and
$\Theta _{\mathrm {Kh}}(P_{2,-3})$ and ![]() $\mathrm {A}_{\mathrm {Kh}}(P_{2,-3})$ are intervals containing
$\mathrm {A}_{\mathrm {Kh}}(P_{2,-3})$ are intervals containing ![]() $0$ with endpoints
$0$ with endpoints ![]() $-2$ and
$-2$ and ![]() $\infty$ and we know that those intervals agree by Proposition 1.10. Since there is a rational component of
$\infty$ and we know that those intervals agree by Proposition 1.10. Since there is a rational component of ![]() $\widetilde {\operatorname {Kh}}(P_{2,-3})$ of slope
$\widetilde {\operatorname {Kh}}(P_{2,-3})$ of slope ![]() $-2$, the endpoint
$-2$, the endpoint ![]() $-2$ is not contained in this interval; for the opposite reason,
$-2$ is not contained in this interval; for the opposite reason, ![]() $\infty$ is contained in the interval. In summary,
$\infty$ is contained in the interval. In summary, ![]() $\Theta _{\mathrm {Kh}}(P_{2,-3})=\mathrm {A}_{\mathrm {Kh}}(P_{2,-3})=(-2,\infty ]$; see Figure 20. As a check, one might consider the knot
$\Theta _{\mathrm {Kh}}(P_{2,-3})=\mathrm {A}_{\mathrm {Kh}}(P_{2,-3})=(-2,\infty ]$; see Figure 20. As a check, one might consider the knot ![]() $P_{2,-3}(-3)$: This pretzel knot is the knot
$P_{2,-3}(-3)$: This pretzel knot is the knot ![]() $8_{19}$ in the Rolfsen knot table, which is the first non-thin knot encountered in enumerated examples.
$8_{19}$ in the Rolfsen knot table, which is the first non-thin knot encountered in enumerated examples.
Table 1. Some prime Conway tangles ![]() $T$, their invariants
$T$, their invariants ![]() $\widetilde {\operatorname {Kh}}(T)$ and
$\widetilde {\operatorname {Kh}}(T)$ and ![]() $\operatorname {HFT}(T)$, and their spaces of thin rational fillings. The polynomial expressions in
$\operatorname {HFT}(T)$, and their spaces of thin rational fillings. The polynomial expressions in ![]() $\delta _{-}$ are the Poincaré polynomials that indicate how often the respective curves appear in which gradings in the invariants. In all examples
$\delta _{-}$ are the Poincaré polynomials that indicate how often the respective curves appear in which gradings in the invariants. In all examples ![]() $\Theta _{\mathrm {HF}}(T)=\Theta _{\mathrm {Kh}}(T)$. For
$\Theta _{\mathrm {HF}}(T)=\Theta _{\mathrm {Kh}}(T)$. For ![]() $\operatorname {HFT}$, an entry
$\operatorname {HFT}$, an entry ![]() $\mathbf {s}_4(\infty )$ represents a conjugate pair of special curves
$\mathbf {s}_4(\infty )$ represents a conjugate pair of special curves ![]() $\mathbf {s}_1(\infty ;{\mathsf {1}},{\mathsf {2}})$ and
$\mathbf {s}_1(\infty ;{\mathsf {1}},{\mathsf {2}})$ and ![]() $\mathbf {s}_1(\infty ;{\mathsf {3}},{\mathsf {4}})$ in identical
$\mathbf {s}_1(\infty ;{\mathsf {3}},{\mathsf {4}})$ in identical ![]() $\delta$-gradings. The computations for
$\delta$-gradings. The computations for ![]() $\widetilde {\operatorname {Kh}}$ were made using the program [Reference ZibrowiusZib21]; for the raw data and the tangle orientations used to fix the absolute
$\widetilde {\operatorname {Kh}}$ were made using the program [Reference ZibrowiusZib21]; for the raw data and the tangle orientations used to fix the absolute ![]() $\delta$-grading, see [Reference Kotelskiy, Watson and ZibrowiusKWZ21a]. The computations of
$\delta$-grading, see [Reference Kotelskiy, Watson and ZibrowiusKWZ21a]. The computations of ![]() $\operatorname {HFT}(Q_0)$ and
$\operatorname {HFT}(Q_0)$ and ![]() $\operatorname {HFT}(P_{2,-3})$ can be found in [Reference ZibrowiusZib20]. Here
$\operatorname {HFT}(P_{2,-3})$ can be found in [Reference ZibrowiusZib20]. Here ![]() $\operatorname {HFT}(P_{2,-2})$ and
$\operatorname {HFT}(P_{2,-2})$ and ![]() $\operatorname {HFT}(T_{4_1})$ were computed using the Mathematica packages [Reference ZibrowiusZib18b] and [Reference ZibrowiusZib18a], respectively. In all cases, the absolute
$\operatorname {HFT}(T_{4_1})$ were computed using the Mathematica packages [Reference ZibrowiusZib18b] and [Reference ZibrowiusZib18a], respectively. In all cases, the absolute ![]() $\delta$-grading on
$\delta$-grading on ![]() $\operatorname {HFT}$ was chosen such that it matches that on
$\operatorname {HFT}$ was chosen such that it matches that on ![]() $\widetilde {\operatorname {Kh}}$.
$\widetilde {\operatorname {Kh}}$.

The Heegaard Floer invariant ![]() $\operatorname {HFT}(P_{2,-3})$ consists of a single rational component (with trivial local system) of slope
$\operatorname {HFT}(P_{2,-3})$ consists of a single rational component (with trivial local system) of slope ![]() $-2$ and a conjugate pair of special components of slope
$-2$ and a conjugate pair of special components of slope ![]() $\infty$; see Table 1. Repeating the same arguments as above, we see that
$\infty$; see Table 1. Repeating the same arguments as above, we see that ![]() $\Theta _{\mathrm {HF}}(P_{2,-3})=\mathrm {A}_{\mathrm {HF}}(P_{2,-3})=(-2,\infty ]$.
$\Theta _{\mathrm {HF}}(P_{2,-3})=\mathrm {A}_{\mathrm {HF}}(P_{2,-3})=(-2,\infty ]$.
We can now revisit the observations made about alternating fillings in this setting: as indicated in Figure 20, there is a sequence of three alternating tangle fillings given by ![]() $-1$,
$-1$, ![]() $0$, and
$0$, and ![]() $+1$. Thus, a transformation of the plane taking either of
$+1$. Thus, a transformation of the plane taking either of ![]() $\{1,0\}$ or
$\{1,0\}$ or ![]() $\{-1,0\}$ to
$\{-1,0\}$ to ![]() $\{\infty, 0\}$ (compare with Figure 17) together with an application of Proposition 7.3 gives two infinite collections of alternating fillings. Expressed in the framing shown, there is a subset of alternating fillings
$\{\infty, 0\}$ (compare with Figure 17) together with an application of Proposition 7.3 gives two infinite collections of alternating fillings. Expressed in the framing shown, there is a subset of alternating fillings ![]() $[-1,1]\subset (-2,\infty ]=\Theta (P_{2,-3})$. More generally, we remark that the subset
$[-1,1]\subset (-2,\infty ]=\Theta (P_{2,-3})$. More generally, we remark that the subset ![]() $[-1,\infty ]\subset (-2,\infty ]$ gives rise to an infinite family of quasi-alternating fillings (this is established in [Reference WatsonWat11]). Of course, adding a single positive twist to the top of the
$[-1,\infty ]\subset (-2,\infty ]$ gives rise to an infinite family of quasi-alternating fillings (this is established in [Reference WatsonWat11]). Of course, adding a single positive twist to the top of the ![]() $(2,-3)$-pretzel tangle yields the
$(2,-3)$-pretzel tangle yields the ![]() $(-2,-3)$-pretzel tangle
$(-2,-3)$-pretzel tangle ![]() $P_{-2,-3}$. The invariant
$P_{-2,-3}$. The invariant ![]() $\widetilde {\operatorname {Kh}}(P_{-2,-3})$ is obtained from a plane shear as shown in Figure 17, so that
$\widetilde {\operatorname {Kh}}(P_{-2,-3})$ is obtained from a plane shear as shown in Figure 17, so that ![]() $\Theta (P_{-2,-3})=(2,1]\subset \operatorname {\mathbb {Q}P}^1$.
$\Theta (P_{-2,-3})=(2,1]\subset \operatorname {\mathbb {Q}P}^1$.
7.4 Bar-Natan curves
In the context of Khovanov invariants, thinness can also be defined in terms of Bar-Natan homology, a generalization of Khovanov homology taking the form of a bigraded ![]() ${\mathbf {k}}[H]$-module. Recall that for a (pointed) link
${\mathbf {k}}[H]$-module. Recall that for a (pointed) link ![]() $L$ with
$L$ with ![]() $|L|$ components, we have that
$|L|$ components, we have that ![]() $\widetilde {\operatorname {BN}}(L)\cong {\mathbf {k}}[H]^{2^{|L|-1}}\oplus H$-torsion. If
$\widetilde {\operatorname {BN}}(L)\cong {\mathbf {k}}[H]^{2^{|L|-1}}\oplus H$-torsion. If ![]() $L$ is a knot, the quantum grading of the term
$L$ is a knot, the quantum grading of the term ![]() ${\mathbf {k}}[H]\subset \widetilde {\operatorname {BN}}(K)$ agrees with Rasmussen's
${\mathbf {k}}[H]\subset \widetilde {\operatorname {BN}}(K)$ agrees with Rasmussen's ![]() $s$-invariant over
$s$-invariant over ![]() ${\mathbf {k}}$. In this subsection we make some general observations that hold over any field
${\mathbf {k}}$. In this subsection we make some general observations that hold over any field ![]() ${\mathbf {k}}$.
${\mathbf {k}}$.
Definition 7.5 We call a ![]() $\delta$-graded
$\delta$-graded ![]() ${\mathbf {k}}[H]$-module
${\mathbf {k}}[H]$-module ![]() $M$ thin if the
$M$ thin if the ![]() $H$-torsion part of
$H$-torsion part of ![]() $M$ and a homogeneous generating set of the free part of
$M$ and a homogeneous generating set of the free part of ![]() $M$ are supported in a single
$M$ are supported in a single ![]() $\delta$-grading.
$\delta$-grading.
It suffices to focus on reduced Khovanov homology, according to the following observation.
Proposition 7.6 For any pointed link ![]() $L$ and field
$L$ and field ![]() ${\mathbf {k}}$,
${\mathbf {k}}$, ![]() $\widetilde {\operatorname {BN}}(L;{\mathbf {k}})$ is thin if and only if
$\widetilde {\operatorname {BN}}(L;{\mathbf {k}})$ is thin if and only if ![]() $\widetilde {\operatorname {Kh}}(L;{\mathbf {k}})$ is thin.
$\widetilde {\operatorname {Kh}}(L;{\mathbf {k}})$ is thin.
Proof. On the level of chain complexes ![]() $\widetilde {\operatorname {CBN}}(L;{\mathbf {k}})$ determines
$\widetilde {\operatorname {CBN}}(L;{\mathbf {k}})$ determines ![]() $\widetilde {\operatorname {CKh}}(L;{\mathbf {k}})$ via a mapping cone formula:
$\widetilde {\operatorname {CKh}}(L;{\mathbf {k}})$ via a mapping cone formula:
Consequently, ![]() $\widetilde {\operatorname {Kh}}(L;{\mathbf {k}})$ is the homology of some map
$\widetilde {\operatorname {Kh}}(L;{\mathbf {k}})$ is the homology of some map
sending each generator of a free summand to itself times ![]() $H$. Therefore, if
$H$. Therefore, if ![]() $\widetilde {\operatorname {BN}}(L;{\mathbf {k}})$ is thin, so is
$\widetilde {\operatorname {BN}}(L;{\mathbf {k}})$ is thin, so is ![]() $\widetilde {\operatorname {Kh}}(L;{\mathbf {k}})$.
$\widetilde {\operatorname {Kh}}(L;{\mathbf {k}})$.
Conversely, suppose ![]() $\widetilde {\operatorname {Kh}}(L;{\mathbf {k}})$ is thin. Recall that
$\widetilde {\operatorname {Kh}}(L;{\mathbf {k}})$ is thin. Recall that ![]() $\widetilde {\operatorname {Kh}}(L;{\mathbf {k}})$ can be promoted to a type D structure
$\widetilde {\operatorname {Kh}}(L;{\mathbf {k}})$ can be promoted to a type D structure ![]() $\widetilde {\operatorname {Kh}}(L;{\mathbf {k}})^{{\mathbf {k}}[H]}$ by connecting pairs of generators by differentials labeled by some powers of
$\widetilde {\operatorname {Kh}}(L;{\mathbf {k}})^{{\mathbf {k}}[H]}$ by connecting pairs of generators by differentials labeled by some powers of ![]() $H$ (see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Sections 3.2 and 3.3, in particular Proposition 3.6]). Since
$H$ (see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Sections 3.2 and 3.3, in particular Proposition 3.6]). Since ![]() $\widetilde {\operatorname {Kh}}(L;{\mathbf {k}})$ is assumed to be thin, the only possible labels are
$\widetilde {\operatorname {Kh}}(L;{\mathbf {k}})$ is assumed to be thin, the only possible labels are ![]() $H$. Together with
$H$. Together with
establishes the result.
We can extract the following from the final steps of the proof.
Corollary 7.7 If ![]() $L$ is a thin link, then the torsion part of the
$L$ is a thin link, then the torsion part of the ![]() ${\mathbf {k}}[H]$-module
${\mathbf {k}}[H]$-module ![]() $\widetilde {\operatorname {BN}}(L;{\mathbf {k}})$ agrees with
$\widetilde {\operatorname {BN}}(L;{\mathbf {k}})$ agrees with ![]() $\ker (H)$. In particular,
$\ker (H)$. In particular, ![]() $2\operatorname {rk}(\ker H)+ 2^{|L|-1} = \det (L)$.
$2\operatorname {rk}(\ker H)+ 2^{|L|-1} = \det (L)$.
As a result, it is possible to define A-links in terms of Bar-Natan homology.
Definition 7.8 Let ![]() $N$ be the dimension of the torsion part of the
$N$ be the dimension of the torsion part of the ![]() ${\mathbf {k}}[H]$-module
${\mathbf {k}}[H]$-module ![]() $\widetilde {\operatorname {BN}}(L;{\mathbf {k}})$ as a
$\widetilde {\operatorname {BN}}(L;{\mathbf {k}})$ as a ![]() ${\mathbf {k}}$-vector space. Then
${\mathbf {k}}$-vector space. Then ![]() $L$ is an A-link whenever
$L$ is an A-link whenever ![]() $2N+2^{|L|-1}=\det (L)$.
$2N+2^{|L|-1}=\det (L)$.
Of course, assuming full support in the sense of Definition 1.4, we have that (Bar-Natan) A-links are (Bar-Natan) thin links. One can also check that this definition of A-link agrees with the definition given in the introduction asking that the total dimension of the reduced Khovanov homology agree with the determinant of the link.
The reduced Bar-Natan homology ![]() $\widetilde {\operatorname {BN}}(T)$ of a Conway tangle
$\widetilde {\operatorname {BN}}(T)$ of a Conway tangle ![]() $T$ satisfies a gluing theorem similar to that for
$T$ satisfies a gluing theorem similar to that for ![]() $\widetilde {\operatorname {Kh}}$ (see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Theorem 7.2]):
$\widetilde {\operatorname {Kh}}$ (see [Reference Kotelskiy, Watson and ZibrowiusKWZ19, Theorem 7.2]):
Here, the right-hand side denotes the wrapped Lagrangian Floer homology of the two tangle invariants. As Example 5.4 illustrates, and as we reiterate here, the components of the multicurve ![]() $\widetilde {\operatorname {BN}}(T)$ need not be linear. If the multicurve consists of just a single component, this allows us to compute the space of thin fillings very easily from the space of tangent slopes.
$\widetilde {\operatorname {BN}}(T)$ need not be linear. If the multicurve consists of just a single component, this allows us to compute the space of thin fillings very easily from the space of tangent slopes.
We illustrate how this is done in the example of the curve ![]() $\widetilde {\operatorname {BN}}(P_{2,-3})$ for the
$\widetilde {\operatorname {BN}}(P_{2,-3})$ for the ![]() $(2,-3)$-pretzel tangle
$(2,-3)$-pretzel tangle ![]() $P_{2,-3}$ from Figure 13. A lift
$P_{2,-3}$ from Figure 13. A lift ![]() $\tilde {\gamma }$ of this curve to
$\tilde {\gamma }$ of this curve to ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ is redrawn in Figure 21. Consider the family of ‘
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ is redrawn in Figure 21. Consider the family of ‘![]() $\varepsilon$-peg-board representatives’
$\varepsilon$-peg-board representatives’ ![]() $\tilde {\gamma }_\varepsilon$ of
$\tilde {\gamma }_\varepsilon$ of ![]() $\tilde {\gamma }$, i.e. representatives of the homotopy class of
$\tilde {\gamma }$, i.e. representatives of the homotopy class of ![]() $\tilde {\gamma }$ which have minimal length among all representatives of distance
$\tilde {\gamma }$ which have minimal length among all representatives of distance ![]() $\varepsilon \in (0,{1}/{2})$ to all punctures in
$\varepsilon \in (0,{1}/{2})$ to all punctures in ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ except the two punctures at the ends of
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ except the two punctures at the ends of ![]() $\tilde {\gamma }$. Following [Reference Hanselman, Rasmussen and WatsonHRW24], the intuition behind this definition is to think of the punctures of
$\tilde {\gamma }$. Following [Reference Hanselman, Rasmussen and WatsonHRW24], the intuition behind this definition is to think of the punctures of ![]() $\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ as pegs of radii
$\mathbb {R}^2\smallsetminus \mathbb {Z}^2$ as pegs of radii ![]() $\varepsilon$ and to imagine pulling the curve
$\varepsilon$ and to imagine pulling the curve ![]() $\tilde {\gamma }$ ‘tight’, like a rubber band. If
$\tilde {\gamma }$ ‘tight’, like a rubber band. If ![]() $\tau _\varepsilon$ denotes the set of rational tangent slopes of the curve
$\tau _\varepsilon$ denotes the set of rational tangent slopes of the curve ![]() $\tilde {\gamma }_\varepsilon$, then the interior of
$\tilde {\gamma }_\varepsilon$, then the interior of ![]() $\mathrm {A}_{\mathrm {Kh}}(P_{2,-3})$ is equal to the complement of
$\mathrm {A}_{\mathrm {Kh}}(P_{2,-3})$ is equal to the complement of ![]() $\bigcap _{\varepsilon \in (0,{1}/{2})}\tau _{\varepsilon }$. Here, the obstruction to being an A-link is the existence of bigons near the points where the limit curve of
$\bigcap _{\varepsilon \in (0,{1}/{2})}\tau _{\varepsilon }$. Here, the obstruction to being an A-link is the existence of bigons near the points where the limit curve of ![]() $\tilde {\gamma }_\varepsilon$ as
$\tilde {\gamma }_\varepsilon$ as ![]() $\varepsilon \rightarrow 0$ (the ‘singular peg-board representative’) changes its slope; this is illustrated in Figure 22.
$\varepsilon \rightarrow 0$ (the ‘singular peg-board representative’) changes its slope; this is illustrated in Figure 22.

Figure 21. The reduced Khovanov (left) and Bar-Natan (right) invariants associated with the cinqfoil, a thin knot, obtained as the closure of the (reframed) ![]() $(2,-3)$-pretzel tangle. Note that the framing given here is such that the thin filling interval is
$(2,-3)$-pretzel tangle. Note that the framing given here is such that the thin filling interval is ![]() $(0,\infty ]$, as determined by the pulled-tight curve
$(0,\infty ]$, as determined by the pulled-tight curve ![]() ${\vartheta }$ shown for the Bar-Natan invariant on the right.
${\vartheta }$ shown for the Bar-Natan invariant on the right.

Figure 22. The rational filling of ![]() along the slope of the straight line
along the slope of the straight line ![]() is not thin, since the
is not thin, since the ![]() $\delta$-gradings of the two intersection points that are connected by the shaded bigon differ by 1.
$\delta$-gradings of the two intersection points that are connected by the shaded bigon differ by 1.
This bears a strong resemblance to how the space of L-space fillings ![]() $\operatorname {\mathcal {L}}(M)$ of a three-manifold
$\operatorname {\mathcal {L}}(M)$ of a three-manifold ![]() $M$ with torus boundary is characterized via the immersed curve invariant
$M$ with torus boundary is characterized via the immersed curve invariant ![]() $\operatorname {\widehat {HF}}(M)$ due to Hanselman, Rasmussen, and the second author. There, it is shown that the interior of
$\operatorname {\widehat {HF}}(M)$ due to Hanselman, Rasmussen, and the second author. There, it is shown that the interior of ![]() $\operatorname {\mathcal {L}}(M)$ is equal to the complement of the space of rational tangent slopes of the singular peg-board representative of
$\operatorname {\mathcal {L}}(M)$ is equal to the complement of the space of rational tangent slopes of the singular peg-board representative of ![]() $\operatorname {\widehat {HF}}(M)$ (see [Reference Hanselman, Rasmussen and WatsonHRW24, Theorem 7.17]).
$\operatorname {\widehat {HF}}(M)$ (see [Reference Hanselman, Rasmussen and WatsonHRW24, Theorem 7.17]).
7.5 A-links and L-spaces
Given a link ![]() $L$, let
$L$, let ![]() $\boldsymbol {\Sigma }_L$ denote the two-fold branched cover of
$\boldsymbol {\Sigma }_L$ denote the two-fold branched cover of ![]() $S^3$ with branch set
$S^3$ with branch set ![]() $L$. (Similarly, we use
$L$. (Similarly, we use ![]() $\boldsymbol {\Sigma }_T$ to denote the two-fold branched cover of
$\boldsymbol {\Sigma }_T$ to denote the two-fold branched cover of ![]() $B^3$ with branch set the tangle arcs of
$B^3$ with branch set the tangle arcs of ![]() $T$.) Owing to the fact that
$T$.) Owing to the fact that ![]() $\widetilde {\operatorname {Kh}}(L^*)$ arises as the
$\widetilde {\operatorname {Kh}}(L^*)$ arises as the ![]() $E_2$-page of a spectral sequence computing
$E_2$-page of a spectral sequence computing ![]() $\operatorname {\widehat {HF}}(\boldsymbol {\Sigma }_L)$ (see [Reference Ozsváth and SzabóOS05b]), one might naturally wonder about the relationship between L-spaces and A-links. In particular, one expects an interplay between
$\operatorname {\widehat {HF}}(\boldsymbol {\Sigma }_L)$ (see [Reference Ozsváth and SzabóOS05b]), one might naturally wonder about the relationship between L-spaces and A-links. In particular, one expects an interplay between ![]() $\mathrm {A}_{\mathrm {Kh}}(T)$ and
$\mathrm {A}_{\mathrm {Kh}}(T)$ and ![]() $\operatorname {\mathcal {L}}(\boldsymbol {\Sigma }_T)$. Before exploring this relationship further, we make some general comments about the definition of L-spaces. In § 1, L-spaces were introduced as solutions of the identity
$\operatorname {\mathcal {L}}(\boldsymbol {\Sigma }_T)$. Before exploring this relationship further, we make some general comments about the definition of L-spaces. In § 1, L-spaces were introduced as solutions of the identity
Usually, L-spaces are defined in terms of the following two conditions:
(a) being a rational homology sphere, that is
 $b_1(Y)=0$; and
$b_1(Y)=0$; and(b) satisfying
 $\dim \operatorname {\widehat {HF}}(Y) = |H_1(Y;\mathbb {Z})|$.
$\dim \operatorname {\widehat {HF}}(Y) = |H_1(Y;\mathbb {Z})|$.
Coefficients are often chosen to be in ![]() $\mathbb {F}$; we do the same and suppress
$\mathbb {F}$; we do the same and suppress ![]() $\mathbb {F}$ in our notation. We observe that these two definitions are equivalent. For rational homology spheres we have the equality
$\mathbb {F}$ in our notation. We observe that these two definitions are equivalent. For rational homology spheres we have the equality ![]() $\chi \operatorname {\widehat {HF}}(Y)=|H_1(Y;\mathbb {Z})|$ and if
$\chi \operatorname {\widehat {HF}}(Y)=|H_1(Y;\mathbb {Z})|$ and if ![]() $b_1(Y)>0$ then
$b_1(Y)>0$ then ![]() $\chi \operatorname {\widehat {HF}}(Y)=0$ (see [Reference Ozsváth and SzabóOS04c]). Thus, it suffices to show the following.
$\chi \operatorname {\widehat {HF}}(Y)=0$ (see [Reference Ozsváth and SzabóOS04c]). Thus, it suffices to show the following.
Proposition 7.9 The Heegaard Floer homology ![]() $\operatorname {\widehat {HF}}(Y)$ does not vanish for any three-manifold
$\operatorname {\widehat {HF}}(Y)$ does not vanish for any three-manifold ![]() $Y$.
$Y$.
We are not aware of a reference for this fact in the literature; Jake Rasmussen suggested the following argument.
Proof of Proposition 7.9 By the definition of ![]() $\operatorname {HF}^\infty (Y)$ as the homology of
$\operatorname {HF}^\infty (Y)$ as the homology of ![]() $\operatorname {\widehat {CF}}(Y)\otimes {\mathbb {F}}[U,U^{-1}]$ with higher differentials, there exists a spectral sequence from
$\operatorname {\widehat {CF}}(Y)\otimes {\mathbb {F}}[U,U^{-1}]$ with higher differentials, there exists a spectral sequence from ![]() $\operatorname {\widehat {HF}}(Y)\otimes {\mathbb {F}}[U,U^{-1}]$ to
$\operatorname {\widehat {HF}}(Y)\otimes {\mathbb {F}}[U,U^{-1}]$ to ![]() $\operatorname {HF}^\infty (Y)$. Therefore, it suffices to show that
$\operatorname {HF}^\infty (Y)$. Therefore, it suffices to show that ![]() $\operatorname {HF}^\infty (Y)$ does not vanish. Lidman computed these groups for all closed orientable three-manifolds [Reference LidmanLid10, Theorem 1.1]; compare with [Reference Ozsváth and SzabóOS03b, Conjecture 4.10]. He showed that for any torsion
$\operatorname {HF}^\infty (Y)$ does not vanish. Lidman computed these groups for all closed orientable three-manifolds [Reference LidmanLid10, Theorem 1.1]; compare with [Reference Ozsváth and SzabóOS03b, Conjecture 4.10]. He showed that for any torsion ![]() $\operatorname {Spin^\textit {c}}$-structure
$\operatorname {Spin^\textit {c}}$-structure ![]() $\mathfrak {s}$, one can write
$\mathfrak {s}$, one can write ![]() $\operatorname {HF}^\infty (Y,\mathfrak {s})$ as the homology of a chain complex whose underlying chain module is equal to
$\operatorname {HF}^\infty (Y,\mathfrak {s})$ as the homology of a chain complex whose underlying chain module is equal to
and with differential of the form
(Torsion ![]() $\operatorname {Spin^\textit {c}}$-structures always exist: it suffices to recall that isomorphism classes of oriented plane fields on a closed and oriented three-manifold are determined by elements of
$\operatorname {Spin^\textit {c}}$-structures always exist: it suffices to recall that isomorphism classes of oriented plane fields on a closed and oriented three-manifold are determined by elements of ![]() $H^2(Y;\mathbb {Z})$, and choose a plane-field on
$H^2(Y;\mathbb {Z})$, and choose a plane-field on ![]() $Y$ with vanishing Euler class.) In particular, the quotient
$Y$ with vanishing Euler class.) In particular, the quotient ![]() $Q$ obtained from
$Q$ obtained from ![]() $\operatorname {HF}^\infty (Y,\mathfrak {s})$ by setting
$\operatorname {HF}^\infty (Y,\mathfrak {s})$ by setting ![]() $U=1$ is the homology of a chain complex whose underlying chain module is
$U=1$ is the homology of a chain complex whose underlying chain module is
and whose differential lowers the grading of the exterior product by 3. The Euler characteristic of this complex is
Note that this value remains invariant under taking homology. Thus, the Euler characteristic of the quotient ![]() $Q$ is equal to the Euler characteristic of
$Q$ is equal to the Euler characteristic of ![]() $\Lambda ^*(H^1(Y;\mathbb {Z}))\otimes \mathbb {F}$, which is equal to
$\Lambda ^*(H^1(Y;\mathbb {Z}))\otimes \mathbb {F}$, which is equal to
where ![]() $a = \dim (H^1(Y;\mathbb {Z})\otimes \mathbb {F})$. This element is non-zero, which can be seen by embedding
$a = \dim (H^1(Y;\mathbb {Z})\otimes \mathbb {F})$. This element is non-zero, which can be seen by embedding ![]() $R$ into the complex plane. Thus,
$R$ into the complex plane. Thus, ![]() $Q$ is non-zero, and so is
$Q$ is non-zero, and so is ![]() $\operatorname {HF}^\infty (Y,\mathfrak {s})$.
$\operatorname {HF}^\infty (Y,\mathfrak {s})$.
In the introduction, we pointed out a close relationship between Khovanov A-links and L-spaces.
Theorem 7.10 If ![]() $L$ is a Khovanov A-link then the two-fold branched cover
$L$ is a Khovanov A-link then the two-fold branched cover ![]() $\boldsymbol {\Sigma }_L$ is an L-space.
$\boldsymbol {\Sigma }_L$ is an L-space.
Proof. The Ozsváth–Szabó spectral sequence [Reference Ozsváth and SzabóOS05b] from ![]() $\widetilde {\operatorname {Kh}}(L^*)$ to
$\widetilde {\operatorname {Kh}}(L^*)$ to ![]() $\operatorname {\widehat {HF}}(\boldsymbol {\Sigma }_L)$ implies that
$\operatorname {\widehat {HF}}(\boldsymbol {\Sigma }_L)$ implies that
so the claim follows from the fact that A-links satisfy ![]() $\dim \widetilde {\operatorname {Kh}}(L)=\det (L)$.
$\dim \widetilde {\operatorname {Kh}}(L)=\det (L)$.
Corollary 7.11 For any Conway tangle ![]() $T$,
$T$, ![]() $\mathrm {A}_{\mathrm {Kh}}(T)\subseteq \operatorname {\mathcal {L}}(\boldsymbol {\Sigma }_T)$.
$\mathrm {A}_{\mathrm {Kh}}(T)\subseteq \operatorname {\mathcal {L}}(\boldsymbol {\Sigma }_T)$.
When ![]() $\operatorname {\mathcal {L}}(\boldsymbol {\Sigma }_L)$ is a closed interval, this inclusion appears to be strict, in general. For instance, consider the now-familiar example of the pretzel tangle
$\operatorname {\mathcal {L}}(\boldsymbol {\Sigma }_L)$ is a closed interval, this inclusion appears to be strict, in general. For instance, consider the now-familiar example of the pretzel tangle ![]() $P_{2,-3}$. The two-fold branched cover of this tangle is homeomorphic to the complement of the right-hand trefoil; the Seifert structure on this knot complement (two Seifert fibred solid tori glued along an essential annulus) is encoded by the sum of rational tangles generating this pretzel. (This is described in more detail and exploited in [Reference WatsonWat12], for example.) These observations are collected in Figure 23, together with the Bar-Natan curve invariant and the curve corresponding to
$P_{2,-3}$. The two-fold branched cover of this tangle is homeomorphic to the complement of the right-hand trefoil; the Seifert structure on this knot complement (two Seifert fibred solid tori glued along an essential annulus) is encoded by the sum of rational tangles generating this pretzel. (This is described in more detail and exploited in [Reference WatsonWat12], for example.) These observations are collected in Figure 23, together with the Bar-Natan curve invariant and the curve corresponding to ![]() $\operatorname {\widehat {HF}}(M)$, where
$\operatorname {\widehat {HF}}(M)$, where ![]() $M=\boldsymbol {\Sigma }_{P_{2,-3}}$ is the complement of the right-hand trefoil. The important thing to check, which accounts for our change of framing on the tangle, is that the
$M=\boldsymbol {\Sigma }_{P_{2,-3}}$ is the complement of the right-hand trefoil. The important thing to check, which accounts for our change of framing on the tangle, is that the ![]() $0$-filling of
$0$-filling of ![]() $P_{2,-3}$ coincides with the
$P_{2,-3}$ coincides with the ![]() $+6$-surgery on the right-hand trefoil. Let
$+6$-surgery on the right-hand trefoil. Let ![]() $P^{\lambda }_{2,-3}$ denote the reframed tangle, that is, the tangle
$P^{\lambda }_{2,-3}$ denote the reframed tangle, that is, the tangle ![]() $P_{2,-3}$ with the six additional half-twists, so that the
$P_{2,-3}$ with the six additional half-twists, so that the ![]() $0$-closure of the tangle is the branch set for
$0$-closure of the tangle is the branch set for ![]() $0$-surgery on the trefoil. We have shown that
$0$-surgery on the trefoil. We have shown that

Figure 23. Comparing the invariant ![]() $\widetilde {\operatorname {BN}}(P^\lambda _{2,-3})$ with the invariant
$\widetilde {\operatorname {BN}}(P^\lambda _{2,-3})$ with the invariant ![]() $\operatorname {\widehat {HF}}(M)$, where
$\operatorname {\widehat {HF}}(M)$, where ![]() $M$ is the complement of the right-hand trefoil. Note that
$M$ is the complement of the right-hand trefoil. Note that ![]() $M$ is homeomorphic to the two-fold branched cover of
$M$ is homeomorphic to the two-fold branched cover of ![]() $P^\lambda _{2,-3}$; the framing is such that the Seifert longitude descends to the arc labeled
$P^\lambda _{2,-3}$; the framing is such that the Seifert longitude descends to the arc labeled ![]() $\lambda$ and the meridian descends to the arc labeled
$\lambda$ and the meridian descends to the arc labeled ![]() $\mu$.
$\mu$.
This example fits into a simple infinite family, observing that the ![]() $(2,2n+1)$ torus knots (for integers
$(2,2n+1)$ torus knots (for integers ![]() $n>0$) have complements that branch double cover an infinite family of tangles. Denote the former by
$n>0$) have complements that branch double cover an infinite family of tangles. Denote the former by ![]() $T_{(2,2n+1)}$ and the latter by
$T_{(2,2n+1)}$ and the latter by ![]() $T_n$, so that
$T_n$, so that ![]() $T_1$ agrees with
$T_1$ agrees with ![]() $P_{2,-3}$ (appropriately reframed); see Figure 24. Since the Seifert genus of
$P_{2,-3}$ (appropriately reframed); see Figure 24. Since the Seifert genus of ![]() $T_{(2,2n+1)}$ is
$T_{(2,2n+1)}$ is ![]() $n$, we compute
$n$, we compute

Figure 24. A tangle ![]() $T_n$ whose two-fold branched cover is the exterior of the torus knot
$T_n$ whose two-fold branched cover is the exterior of the torus knot ![]() $T_{(2,2n+1)}$. Note that in the case
$T_{(2,2n+1)}$. Note that in the case ![]() $n=1$, we recover the right-hand trefoil. The image of the slope
$n=1$, we recover the right-hand trefoil. The image of the slope ![]() $\lambda +4n\mu$ descends to the arc indicated on the tangle boundary.
$\lambda +4n\mu$ descends to the arc indicated on the tangle boundary.
In particular, the interval of L-space fillings on a given knot (with fixed strong inversion) that do not branch over a thin link can be made arbitrarily large: it is ![]() $[2n-1,4n]$, for these examples. A compelling pattern emerges, and one might reasonably ask about the relationship between the curves
$[2n-1,4n]$, for these examples. A compelling pattern emerges, and one might reasonably ask about the relationship between the curves ![]() $\widetilde {\operatorname {BN}}(T)$ and
$\widetilde {\operatorname {BN}}(T)$ and ![]() $\operatorname {\widehat {HF}}(\boldsymbol {\Sigma }_T)$ in general; see also [Reference Hanselman, Rasmussen and WatsonHRW22, Section 7] for another point of view.
$\operatorname {\widehat {HF}}(\boldsymbol {\Sigma }_T)$ in general; see also [Reference Hanselman, Rasmussen and WatsonHRW22, Section 7] for another point of view.
7.6 Other manifolds admitting a strong inversion
The principle exploited above can be thought of as the Montesinos trick: given a strongly invertible knot ![]() $K$, there is an involution on the complement
$K$, there is an involution on the complement ![]() $M=S^3\setminus K$ with quotient a tangle
$M=S^3\setminus K$ with quotient a tangle ![]() $T$. (This is the idea behind the enumeration of tangles given in [Reference Kotelskiy, Watson and ZibrowiusKWZ22].) This tangle will always have the property of being cap trivial, that is, the
$T$. (This is the idea behind the enumeration of tangles given in [Reference Kotelskiy, Watson and ZibrowiusKWZ22].) This tangle will always have the property of being cap trivial, that is, the ![]() $\infty$-filling of
$\infty$-filling of ![]() $T$ is unknotted. For example, we saw in § 7.1 that
$T$ is unknotted. For example, we saw in § 7.1 that ![]() $\boldsymbol {\Sigma }_{Q_0}$ is the complement of the trivial knot, and each non-zero filling gives a lens space, which branch double-covers the given two-bridge knot. Thus, as a result,
$\boldsymbol {\Sigma }_{Q_0}$ is the complement of the trivial knot, and each non-zero filling gives a lens space, which branch double-covers the given two-bridge knot. Thus, as a result, ![]() $\operatorname {\mathcal {L}}(\boldsymbol {\Sigma }_{Q_0})=\operatorname {\mathbb {Q}P}^1\smallsetminus \{0\}$.
$\operatorname {\mathcal {L}}(\boldsymbol {\Sigma }_{Q_0})=\operatorname {\mathbb {Q}P}^1\smallsetminus \{0\}$.
We have also seen that the exterior of the right-hand trefoil is the two-fold branched cover of ![]() $P_{2,-3}$. This same trick applies to any knot admitting a strong inversion. Here is another example: the exterior of the figure-eight knot is the two-fold branched cover of a tangle which we denote by
$P_{2,-3}$. This same trick applies to any knot admitting a strong inversion. Here is another example: the exterior of the figure-eight knot is the two-fold branched cover of a tangle which we denote by ![]() $T_{4_1}$. (In fact, there are two strong inversions on this knot, but in this case changing the choice of one for the other results in the mirror image of the tangle.) The rational filling along slope
$T_{4_1}$. (In fact, there are two strong inversions on this knot, but in this case changing the choice of one for the other results in the mirror image of the tangle.) The rational filling along slope ![]() $\infty$ results in an unknot, by construction, so this is a thin filling. However, in both the Heegaard Floer and the Khovanov setting, this is the only A-link filling. This is because both
$\infty$ results in an unknot, by construction, so this is a thin filling. However, in both the Heegaard Floer and the Khovanov setting, this is the only A-link filling. This is because both ![]() $\widetilde {\operatorname {Kh}}(T_{4_1})$ and
$\widetilde {\operatorname {Kh}}(T_{4_1})$ and ![]() $\operatorname {HFT}(T_{4_1})$ contain special components of slope
$\operatorname {HFT}(T_{4_1})$ contain special components of slope ![]() $\infty$ in adjacent
$\infty$ in adjacent ![]() $\delta$-gradings. It is also remarkable that the two special components of
$\delta$-gradings. It is also remarkable that the two special components of ![]() $\widetilde {\operatorname {Kh}}(T_{4_1})$ correspond to the two conjugate pairs of special curves in
$\widetilde {\operatorname {Kh}}(T_{4_1})$ correspond to the two conjugate pairs of special curves in ![]() $\operatorname {HFT}(T_{4_1})$ and the rational components of the invariants have the same slope. On the Khovanov side, the lack of thin fillings is consistent: the cover
$\operatorname {HFT}(T_{4_1})$ and the rational components of the invariants have the same slope. On the Khovanov side, the lack of thin fillings is consistent: the cover ![]() $\boldsymbol {\Sigma }_{T_{4_1}}$ is homeomorphic to the exterior of the figure-eight knot, which has no L-space fillings other than the trivial filling.
$\boldsymbol {\Sigma }_{T_{4_1}}$ is homeomorphic to the exterior of the figure-eight knot, which has no L-space fillings other than the trivial filling.
Now consider the pretzel tangle ![]() $P_{2,-2}$; it is an instructive exercise to check that
$P_{2,-2}$; it is an instructive exercise to check that ![]() $\boldsymbol {\Sigma }_{P_{2,-2}}$ is not the exterior of a knot in
$\boldsymbol {\Sigma }_{P_{2,-2}}$ is not the exterior of a knot in ![]() $S^3$. Indeed, this example is not cap trivial; the cover
$S^3$. Indeed, this example is not cap trivial; the cover ![]() $\boldsymbol {\Sigma }_{P_{2,-2}}$ is a Seifert fibred space known as the twisted
$\boldsymbol {\Sigma }_{P_{2,-2}}$ is a Seifert fibred space known as the twisted ![]() $I$-bundle over the Klein bottle. It can be realized as the complement of a knot in
$I$-bundle over the Klein bottle. It can be realized as the complement of a knot in ![]() $S^2\times S^1$. This manifold belongs to a class of manifolds known as Heegaard Floer homology solid tori, which enjoy the property that all fillings, other than the rational longitude filling, are L-spaces. That is,
$S^2\times S^1$. This manifold belongs to a class of manifolds known as Heegaard Floer homology solid tori, which enjoy the property that all fillings, other than the rational longitude filling, are L-spaces. That is, ![]() $\operatorname {\mathcal {L}}(\boldsymbol {\Sigma }_{P_{2,-2}}) =\operatorname {\mathbb {Q}P}^1\setminus \{\infty \}$. From the perspective of tangle invariants this example is quite interesting, because the Heegaard Floer invariant contains a pair of special components that do not correspond to a special component in
$\operatorname {\mathcal {L}}(\boldsymbol {\Sigma }_{P_{2,-2}}) =\operatorname {\mathbb {Q}P}^1\setminus \{\infty \}$. From the perspective of tangle invariants this example is quite interesting, because the Heegaard Floer invariant contains a pair of special components that do not correspond to a special component in ![]() $\widetilde {\operatorname {Kh}}(P_{2,-2})$. For the space of A-link and thin rational fillings, this additional pair of special curves has no consequence; all spaces are equal to
$\widetilde {\operatorname {Kh}}(P_{2,-2})$. For the space of A-link and thin rational fillings, this additional pair of special curves has no consequence; all spaces are equal to ![]() $(-2,2)$ and can be computed from the tangle invariants
$(-2,2)$ and can be computed from the tangle invariants ![]() $\widetilde {\operatorname {Kh}}(P_{2,-2})$ and
$\widetilde {\operatorname {Kh}}(P_{2,-2})$ and ![]() $\operatorname {HFT}(P_{2,-2})$ (following the same strategy as for
$\operatorname {HFT}(P_{2,-2})$ (following the same strategy as for ![]() $P_{2,-3}$). In particular,
$P_{2,-3}$). In particular,
This discussion is summarized in Table 1. In each case, the space of A-link fillings agrees with the space of thin fillings and, perhaps more surprisingly, the spaces agree in both the Heegaard Floer and the Khovanov setting.
7.7 Amalgamation: thin knots containing essential Conway spheres
We can now illustrate what is perhaps the main observation of this paper, that is, the fact that understanding the thin filling slopes for tangles ![]() $T_1$ and
$T_1$ and ![]() $T_2$ allows us to determine when the link
$T_2$ allows us to determine when the link ![]() $T_1\cup T_2$ will be thin. This is shown for our main running example in Figure 25.
$T_1\cup T_2$ will be thin. This is shown for our main running example in Figure 25.
Proposition 7.12 Unions of ![]() $(2,-3)$-pretzel tangles give links that are thin in Khovanov homology if and only if they are thin in Heegaard Floer homology.
$(2,-3)$-pretzel tangles give links that are thin in Khovanov homology if and only if they are thin in Heegaard Floer homology.

Figure 25. A tangle decomposition of a thin knot ![]() $K$ along an essential Conway sphere and its reduced Bar-Natan homology computed from the two tangle invariants. Observe that the spaces of thin fillings of the two tangles are
$K$ along an essential Conway sphere and its reduced Bar-Natan homology computed from the two tangle invariants. Observe that the spaces of thin fillings of the two tangles are ![]() $(-\infty,0]$ and
$(-\infty,0]$ and ![]() $(0,\infty ]$, so their union is indeed
$(0,\infty ]$, so their union is indeed ![]() $\operatorname {\mathbb {Q}P}^1$, in accordance with Theorem 1.15. We expect that the dimensions of knot Floer homology and reduced Khovanov homology in this example are minimal among all knots containing essential Conway spheres. This will be explored in future work.
$\operatorname {\mathbb {Q}P}^1$, in accordance with Theorem 1.15. We expect that the dimensions of knot Floer homology and reduced Khovanov homology in this example are minimal among all knots containing essential Conway spheres. This will be explored in future work.
Proof. Immediate: the set of thin filling slopes agrees in both cases.
While this amounts, essentially, to a single example, we remark that Example 7.14 is the only example we have seen so far in which the spaces of thin fillings do not agree for the two theories, and even in this example, they may actually agree over ![]() $\mathbb {Q}$. Note that one can also check that the thin links obtained in this way are a strict subset of the L-spaces one obtains by gluing a pair of trefoil exteriors together.
$\mathbb {Q}$. Note that one can also check that the thin links obtained in this way are a strict subset of the L-spaces one obtains by gluing a pair of trefoil exteriors together.
7.8 Exotica
The examples collected in Table 1 show that the spaces of A-link and thin rational fillings can be open and half-open intervals. However, they may also be closed intervals, as the tangle ![]() $T_a$ from Table 2 illustrates. The tangle
$T_a$ from Table 2 illustrates. The tangle ![]() $T_b$ from the same table is obtained by taking a tangle sum of two copies of the tangle
$T_b$ from the same table is obtained by taking a tangle sum of two copies of the tangle ![]() $T_{4_1}$ from Table 1 after rotating one of them by
$T_{4_1}$ from Table 1 after rotating one of them by ![]() ${\pi }/{2}$. This tangle does not admit any A-link filling, since its invariants contain special components in adjacent
${\pi }/{2}$. This tangle does not admit any A-link filling, since its invariants contain special components in adjacent ![]() $\delta$-gradings in two distinct slopes. Thus, the space of A-link fillings of a tangle (as well as, consequently, the space of thin fillings) can be either empty, a singleton, an open interval, a half-open interval, or a closed interval. This is in contrast with the space of L-space fillings of a three-manifold with torus boundary, which can only be empty, a singleton, a closed interval, or
$\delta$-gradings in two distinct slopes. Thus, the space of A-link fillings of a tangle (as well as, consequently, the space of thin fillings) can be either empty, a singleton, an open interval, a half-open interval, or a closed interval. This is in contrast with the space of L-space fillings of a three-manifold with torus boundary, which can only be empty, a singleton, a closed interval, or ![]() $\operatorname {\mathbb {Q}P}^1$ minus a point [Reference Rasmussen and RasmussenRR17]. In summary, all types of A-link rational filling spaces from Theorem 1.8 arise in actual examples. We do not know if the same is true for the additional case of precisely two distinct thin rational fillings in Theorem 1.9.
$\operatorname {\mathbb {Q}P}^1$ minus a point [Reference Rasmussen and RasmussenRR17]. In summary, all types of A-link rational filling spaces from Theorem 1.8 arise in actual examples. We do not know if the same is true for the additional case of precisely two distinct thin rational fillings in Theorem 1.9.
Conjecture 7.13 There is no tangle ![]() $T$ such that
$T$ such that ![]() $\Theta _{\mathrm {HF}}(T)$ or
$\Theta _{\mathrm {HF}}(T)$ or ![]() $\Theta _{\mathrm {Kh}}(T)$ consists of two points.
$\Theta _{\mathrm {Kh}}(T)$ consists of two points.
Table 2. Two more prime Conway tangles ![]() $T$, their invariant
$T$, their invariant ![]() $\widetilde {\operatorname {Kh}}(T)$, and the corresponding space of thin rational fillings. The polynomial expressions in
$\widetilde {\operatorname {Kh}}(T)$, and the corresponding space of thin rational fillings. The polynomial expressions in ![]() $ \delta _{-}$ and
$ \delta _{-}$ and ![]() $\delta _{|}$ are the Poincaré polynomials that indicate how often the respective curves appear in which gradings in
$\delta _{|}$ are the Poincaré polynomials that indicate how often the respective curves appear in which gradings in ![]() $ \widetilde {\operatorname {Kh}}(T)$. The computations were made using the program [Reference ZibrowiusZib21]; for the raw data and the tangle orientations used to fix the absolute
$ \widetilde {\operatorname {Kh}}(T)$. The computations were made using the program [Reference ZibrowiusZib21]; for the raw data and the tangle orientations used to fix the absolute ![]() $\delta$-grading, see [Reference Kotelskiy, Watson and ZibrowiusKWZ21a].
$\delta$-grading, see [Reference Kotelskiy, Watson and ZibrowiusKWZ21a].

Example 7.14 From the knot ![]() $16^n_{197566}$ in Example 7.1, one can easily obtain tangles for which the spaces of thin fillings depend on the field of coefficients. For instance, Figure 26 shows a tangle whose rational filling along the slope
$16^n_{197566}$ in Example 7.1, one can easily obtain tangles for which the spaces of thin fillings depend on the field of coefficients. For instance, Figure 26 shows a tangle whose rational filling along the slope ![]() ${5}/{3}$ is equal to
${5}/{3}$ is equal to ![]() $16^n_{197566}$. The Khovanov invariant
$16^n_{197566}$. The Khovanov invariant ![]() $\widetilde {\operatorname {Kh}}$ of this tangle can be summarized as follows, using the same notation as in Tables 1 and 2; see example T_16n197566 in [Reference Kotelskiy, Watson and ZibrowiusKWZ21a]:
$\widetilde {\operatorname {Kh}}$ of this tangle can be summarized as follows, using the same notation as in Tables 1 and 2; see example T_16n197566 in [Reference Kotelskiy, Watson and ZibrowiusKWZ21a]:
 \begin{gather*} \text{over }{\mathbb{F}}_2:\quad \mathbf{s}_4(\infty):16\cdot\delta_{-}^{2}\quad \mathbf{s}_8(\infty):\delta_{-}^{2}\quad \mathbf{r}_1({4}/{3}):\delta_{|}^{3/2} \\ \text{over }{\mathbb{F}}_3:\quad \mathbf{s}_4(\infty):16\cdot\delta_{-}^{2}\quad \mathbf{s}_6(\infty):\delta_{-}^{2}\quad \mathbf{r}_1(2):\delta_{|}^{3/2}\quad \mathbf{r}_2(2):\delta_{|}^{3/2}. \end{gather*}
\begin{gather*} \text{over }{\mathbb{F}}_2:\quad \mathbf{s}_4(\infty):16\cdot\delta_{-}^{2}\quad \mathbf{s}_8(\infty):\delta_{-}^{2}\quad \mathbf{r}_1({4}/{3}):\delta_{|}^{3/2} \\ \text{over }{\mathbb{F}}_3:\quad \mathbf{s}_4(\infty):16\cdot\delta_{-}^{2}\quad \mathbf{s}_6(\infty):\delta_{-}^{2}\quad \mathbf{r}_1(2):\delta_{|}^{3/2}\quad \mathbf{r}_2(2):\delta_{|}^{3/2}. \end{gather*}
Thus, the space of thin fillings of this tangle is equal to ![]() $[\infty,{4}/{3})$ for Khovanov homology over
$[\infty,{4}/{3})$ for Khovanov homology over ![]() ${\mathbb {F}}_2$, but
${\mathbb {F}}_2$, but ![]() $[\infty,2)$ for Khovanov homology over
$[\infty,2)$ for Khovanov homology over ![]() ${\mathbb {F}}_3$. As a result, Shumakovitch's example is part of an infinite family of links: pick any closure of this tangle along a slope
${\mathbb {F}}_3$. As a result, Shumakovitch's example is part of an infinite family of links: pick any closure of this tangle along a slope ![]() $s\in [{4}/{3},2)$.
$s\in [{4}/{3},2)$.
The Heegaard Floer invariant of this tangle is equal to ![]() $\{2\cdot \mathbf {r}(2),\mathbf {r}(4),17\cdot \mathbf {s}_4(\infty )\}$, where
$\{2\cdot \mathbf {r}(2),\mathbf {r}(4),17\cdot \mathbf {s}_4(\infty )\}$, where ![]() $2\cdot \mathbf {s}_4(\infty )$ represents two conjugate pairs of special curves
$2\cdot \mathbf {s}_4(\infty )$ represents two conjugate pairs of special curves ![]() $\mathbf {s}_1(\infty ;{\mathsf {1}},{\mathsf {2}})$ and
$\mathbf {s}_1(\infty ;{\mathsf {1}},{\mathsf {2}})$ and ![]() $\mathbf {s}_1(\infty ;{\mathsf {3}},{\mathsf {4}})$. All special curves and the two rational curves all live in the same
$\mathbf {s}_1(\infty ;{\mathsf {3}},{\mathsf {4}})$. All special curves and the two rational curves all live in the same ![]() $\delta$-grading. Moreover,
$\delta$-grading. Moreover, ![]() $\delta (17\cdot \mathbf {s}_4(\infty ),\mathbf {r}(4))=\delta (\mathbf {r}(4),2\cdot \mathbf {r}(2))=0$. (These computations were done indirectly using [Reference SzabóSza20].) Thus, the space of thin fillings in Heegaard Floer theory is equal to
$\delta (17\cdot \mathbf {s}_4(\infty ),\mathbf {r}(4))=\delta (\mathbf {r}(4),2\cdot \mathbf {r}(2))=0$. (These computations were done indirectly using [Reference SzabóSza20].) Thus, the space of thin fillings in Heegaard Floer theory is equal to ![]() $[\infty,2)$.
$[\infty,2)$.
We are grateful to Matt Hedden for pointing out that knot Floer homology does not have full support; see Figure 27. This example was used by Hedden and Ording to establish that the Ozsváth–Szabó concordance invariant ![]() $\tau$ and the Rasmussen invariant
$\tau$ and the Rasmussen invariant ![]() $s$ do not agree [Reference Hedden and OrdingHO08]. It is interesting to study this example in the context of tangles.
$s$ do not agree [Reference Hedden and OrdingHO08]. It is interesting to study this example in the context of tangles.
Example 7.15 Let ![]() $T$ be the subtangle of the thick A-knot illustrated in Figure 27. We computed the Heegaard Floer invariants of
$T$ be the subtangle of the thick A-knot illustrated in Figure 27. We computed the Heegaard Floer invariants of ![]() $T$ as
$T$ as
Here, ![]() $2\cdot \mathbf {s}_4(\infty )$ represents two conjugate pairs of special curves
$2\cdot \mathbf {s}_4(\infty )$ represents two conjugate pairs of special curves ![]() $\mathbf {s}_1(\infty ;{\mathsf {1}},{\mathsf {2}})$ and
$\mathbf {s}_1(\infty ;{\mathsf {1}},{\mathsf {2}})$ and ![]() $\mathbf {s}_1(\infty ;{\mathsf {3}},{\mathsf {4}})$, which all live in the same
$\mathbf {s}_1(\infty ;{\mathsf {3}},{\mathsf {4}})$, which all live in the same ![]() $\delta$-grading. Moreover,
$\delta$-grading. Moreover, ![]() $\delta (\mathbf {r}(-{5}/{2}),2\cdot \mathbf {s}_4(\infty ))=2$. These computations were done indirectly using [Reference SzabóSza20]. Note, in particular, that
$\delta (\mathbf {r}(-{5}/{2}),2\cdot \mathbf {s}_4(\infty ))=2$. These computations were done indirectly using [Reference SzabóSza20]. Note, in particular, that ![]() $T$ is an example of a Heegaard Floer exceptional tangle (Definition 4.24). Together with Example 2.17, it illustrates that Theorem 4.31 is indeed wrong if we drop the assumption that both tangles not be Heegaard Floer exceptional; see also [Reference ZibrowiusZib23a, Proof of Theorem 1.8]. Thus, it validates the shift in perspective from thin to A-links.
$T$ is an example of a Heegaard Floer exceptional tangle (Definition 4.24). Together with Example 2.17, it illustrates that Theorem 4.31 is indeed wrong if we drop the assumption that both tangles not be Heegaard Floer exceptional; see also [Reference ZibrowiusZib23a, Proof of Theorem 1.8]. Thus, it validates the shift in perspective from thin to A-links.

Figure 27. The knot Floer homology of the 6-twisted Whitehead double of the right-handed trefoil knot (shown on the left) does not have full support, and the subtangle (shown on the right) is Heegaard Floer exceptional.
In contrast, the Khovanov homology of the knot in Figure 27 is not thin and it has full support. Moreover, we compute
 \begin{gather*} \widetilde{\operatorname{Kh}}(T;{\mathbb{F}}_2) =\{\mathbf{r}_1({3}/{2}),8\cdot\mathbf{s}_4(\infty)\}, \quad \mathrm{A}_{\mathrm{HF}}(T;{\mathbb{F}}_2)=\Theta_{\mathrm{HF}}(T;{\mathbb{F}}_2)=\{\infty\} \\ \widetilde{\operatorname{Kh}}(T;{\mathbf{k}}) =\{\mathbf{r}_1(-{1}/{2}),2\cdot\mathbf{s}_4(\infty),6\cdot\mathbf{s}_2(\infty)\}, \quad \mathrm{A}_{\mathrm{HF}}(T;{\mathbf{k}})=\Theta_{\mathrm{HF}}(T;{\mathbf{k}})=\{\infty\}, \end{gather*}
\begin{gather*} \widetilde{\operatorname{Kh}}(T;{\mathbb{F}}_2) =\{\mathbf{r}_1({3}/{2}),8\cdot\mathbf{s}_4(\infty)\}, \quad \mathrm{A}_{\mathrm{HF}}(T;{\mathbb{F}}_2)=\Theta_{\mathrm{HF}}(T;{\mathbb{F}}_2)=\{\infty\} \\ \widetilde{\operatorname{Kh}}(T;{\mathbf{k}}) =\{\mathbf{r}_1(-{1}/{2}),2\cdot\mathbf{s}_4(\infty),6\cdot\mathbf{s}_2(\infty)\}, \quad \mathrm{A}_{\mathrm{HF}}(T;{\mathbf{k}})=\Theta_{\mathrm{HF}}(T;{\mathbf{k}})=\{\infty\}, \end{gather*}
where ![]() ${\mathbf {k}}=\mathbb {Q}, {\mathbb {F}}_3,{\mathbb {F}}_5, {\mathbb {F}}_7, {\mathbb {F}}_{11}$; see example 3_1 in [Reference Kotelskiy, Watson and ZibrowiusKWZ21a]. Here, the special components sit in three consecutive
${\mathbf {k}}=\mathbb {Q}, {\mathbb {F}}_3,{\mathbb {F}}_5, {\mathbb {F}}_7, {\mathbb {F}}_{11}$; see example 3_1 in [Reference Kotelskiy, Watson and ZibrowiusKWZ21a]. Here, the special components sit in three consecutive ![]() $\delta$-gradings.
$\delta$-gradings.
It is interesting that we see three distinct slopes of rational components in this example. This is related to the fact that rational closures of ![]() $T$ not only provide examples for which
$T$ not only provide examples for which ![]() $\tau$ and Rasmussen's original invariant
$\tau$ and Rasmussen's original invariant ![]() $s=s^\mathbb {Q}$ are distinct, but they also include examples for which
$s=s^\mathbb {Q}$ are distinct, but they also include examples for which ![]() $s^\mathbb {Q}\neq s^{{\mathbb {F}}_2}$. This phenomenon is explored further in [Reference Lewark and ZibrowiusLZ21, Reference Lewark and ZibrowiusLZ22].
$s^\mathbb {Q}\neq s^{{\mathbb {F}}_2}$. This phenomenon is explored further in [Reference Lewark and ZibrowiusLZ21, Reference Lewark and ZibrowiusLZ22].
Remark 7.16 As an observation to summarize: In Theorem 1.7, one might ask why the assumption that the two manifolds are boundary incompressible is needed. The answer is that when one of the ![]() $M_i$ is boundary compressible then the condition for L-spaces is
$M_i$ is boundary compressible then the condition for L-spaces is ![]() $\mathcal {L}(M_0) \cup h(\mathcal {L}(M_1)) = \operatorname {\mathbb {Q}P}^1$; consider, for instance, Dehn surgery along the figure-eight knot; for more discussion, see [Reference Hanselman, Rasmussen and WatsonHRW24] and compare with [Reference Hanselman, Rasmussen, Rasmussen and WatsonHRRW20]. In contrast, because the intervals have a wider range of endpoint behaviour in the tangle case, our A-link and thin gluing theorems do not admit cleaner statements if we assume that the tangles are boundary incompressible (i.e. non-split).
$\mathcal {L}(M_0) \cup h(\mathcal {L}(M_1)) = \operatorname {\mathbb {Q}P}^1$; consider, for instance, Dehn surgery along the figure-eight knot; for more discussion, see [Reference Hanselman, Rasmussen and WatsonHRW24] and compare with [Reference Hanselman, Rasmussen, Rasmussen and WatsonHRRW20]. In contrast, because the intervals have a wider range of endpoint behaviour in the tangle case, our A-link and thin gluing theorems do not admit cleaner statements if we assume that the tangles are boundary incompressible (i.e. non-split).
Acknowledgements
The authors thank Antonio Alfieri, Jonathan Hanselman, Matt Hedden, Lukas Lewark, Tye Lidman, Allison Moore, and Jake Rasmussen for helpful conversations.
Conflicts of Interest
None.