Hostname: page-component-77c78cf97d-d2fvj Total loading time: 0 Render date: 2026-04-28T21:36:41.762Z Has data issue: false hasContentIssue false
  • English
  • Français

Thin monodromy in Sp(4)

Part of: Families, fibrations

Published online by Cambridge University Press:  10 March 2014

Christopher Brav  and
Hugh Thomas
Christopher Brav
Affiliation:
Mathematical Institute, University of Oxford, 24–29 St Giles’, Oxford OX1 3LB, UK email brav@maths.ox.ac.uk
Hugh Thomas
Affiliation:
Department of Mathematics and Statistics, University of New Brunswick, Fredericton, New Brunswick, Canada E3B 5A3 email hthomas@unb.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that some hypergeometric monodromy groups in 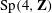${\rm Sp}(4,\mathbf{Z})$ split as free or amalgamated products and hence by cohomological considerations give examples of Zariski dense, non-arithmetic monodromy groups of real rank 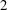$2$. In particular, we show that the monodromy group of the natural quotient of the Dwork family of quintic threefolds in 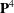$\mathbf{P}^{4}$ splits as 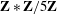$\mathbf{Z}\ast \mathbf{Z}/5\mathbf{Z}$. As a consequence, for a smooth quintic threefold 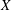$X$ we show that the group of autoequivalences 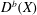$D^{b}(X)$ generated by the spherical twist along 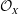${\mathcal{O}}_{X}$ and by tensoring with 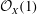${\mathcal{O}}_{X}(1)$ is an Artin group of dihedral type.

Keywords

Dwork familymonodromythin groupsping-pong lemma

MSC classification

Secondary: 14D05: Structure of families (Picard-Lefschetz, monodromy, etc.)

Information

Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 3 , March 2014 , pp. 333 - 343
Copyright
© The Author(s) 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Beukers, F. and Heckman, G., Monodromy for the hypergeometric function nF n−1, Invent. Math. 95 (1989), 325–354; MR 974906 (90f:11034).Google Scholar
Canonaco, A. and Karp, R. L., Derived autoequivalences and a weighted Beilinson resolution, J. Geom. Phys. 58 (2008), 743–760.Google Scholar
Chen, Y.-H., Yang, Y. and Yui, N., Monodromy of Picard–Fuchs differential equations for Calabi–Yau threefolds, J. Reine Angew. Math. 616 (2008), 167–203; with an appendix by Cord Erdenberger; MR 2369490 (2009m:32046).Google Scholar
Deligne, P. and Mostow, G. D., Monodromy of hypergeometric functions and nonlattice integral monodromy, Publ. Math. Inst. Hautes Études Sci. 63 (1986), 5–89; MR 849651 (88a:22023a).Google Scholar
Doran, C. F. and Morgan, J. W., Mirror symmetry and integral variations of Hodge structure underlying one-parameter families of Calabi–Yau threefolds, in Mirror symmetry. V, AMS/IP Studies in Advanced Mathematics, vol. 38 (American Mathematical Society, Providence, RI, 2006), 517–537; MR 2282973 (2008e:14010).Google Scholar
van Enckevort, C. and van Straten, D., Monodromy calculations of fourth order equations of Calabi–Yau type, in Mirror symmetry. V, AMS/IP Studies in Advanced Mathematics, vol. 38 (American Mathematical Society, Providence, RI, 2006), 539–559; MR 2282974 (2007m:14057).Google Scholar
Fuchs, E., Meiri, C. and Sarnak, P., Hyperbolic monodromy groups for the hypergeometric equation and Cartan involutions, Preprint (2013), arXiv:1305.0729.Google Scholar
Griffiths, P. and Schmid, W., Recent developments in Hodge theory: a discussion of techniques and results, in Discrete subgroups of Lie groups and applications to moduli (Internat. Colloq., Bombay, 1973) (Oxford University Press, Bombay, 1975), 31–127; MR 0419850 (54 #7868).Google Scholar
Kuznetsov, A. G., Derived category of a cubic threefold and the variety $V_{14}$, Tr. Mat. Inst. Steklova 246 (2004), no. Algebr. Geom. Metody, Svyazi i Prilozh., 183–207;MR 2101293 (2005i:14049).Google Scholar
Lee, R. and Weintraub, S. H., Cohomology of Sp4(Z)and related groups and spaces, Topology 24 (1985), 391–410; MR 816521 (87b:11044).Google Scholar
Lyndon, R. C. and Schupp, P. E.,Combinatorial group theory, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 89 (Springer, Berlin, 1977); MR 0577064 (58 #28182).Google Scholar
Nori, M. V., A nonarithmetic monodromy group, C. R. Acad. Sci. Paris Sér. I Math. 302 (1986), 71–72; MR 832040 (87g:14008).Google Scholar
Sarnak, P., Notes on thin matrix groups, Preprint (2012), arXiv:1212.3525.Google Scholar
Singh, S. and Venkataramana, T. N., Arithmeticity of certain symplectic hypergeometric groups, Preprint (2012), arXiv:1208.6460.Google Scholar
Stein, W. A. et al. , Sage mathematics software (Version 5.3), The Sage Development Team, 2012, http://www.sagemath.org.Google Scholar
Swan, R. G., Groups of cohomological dimension one, J. Algebra 12 (1969), 585–610; MR 0240177 (39 #1531).Google Scholar