Article contents
Topological K-theory of complex noncommutative spaces
Published online by Cambridge University Press: 22 September 2015
Abstract
The purpose of this work is to give a definition of a topological K-theory for dg-categories over 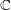 $\mathbb{C}$ and to prove that the Chern character map from algebraic K-theory to periodic cyclic homology descends naturally to this new invariant. This topological Chern map provides a natural candidate for the existence of a rational structure on the periodic cyclic homology of a smooth proper dg-algebra, within the theory of noncommutative Hodge structures. The definition of topological K-theory consists in two steps: taking the topological realization of algebraic K-theory and inverting the Bott element. The topological realization is the left Kan extension of the functor ‘space of complex points’ to all simplicial presheaves over complex algebraic varieties. Our first main result states that the topological K-theory of the unit dg-category is the spectrum
$\mathbb{C}$ and to prove that the Chern character map from algebraic K-theory to periodic cyclic homology descends naturally to this new invariant. This topological Chern map provides a natural candidate for the existence of a rational structure on the periodic cyclic homology of a smooth proper dg-algebra, within the theory of noncommutative Hodge structures. The definition of topological K-theory consists in two steps: taking the topological realization of algebraic K-theory and inverting the Bott element. The topological realization is the left Kan extension of the functor ‘space of complex points’ to all simplicial presheaves over complex algebraic varieties. Our first main result states that the topological K-theory of the unit dg-category is the spectrum 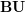 $\mathbf{BU}$. For this we are led to prove a homotopical generalization of Deligne’s cohomological proper descent, using Lurie’s proper descent. The fact that the Chern character descends to topological K-theory is established by using Kassel’s Künneth formula for periodic cyclic homology and the proper descent. In the case of a dg-category of perfect complexes on a separated scheme of finite type, we show that we recover the usual topological K-theory of complex points. We show as well that the Chern map tensorized with
$\mathbf{BU}$. For this we are led to prove a homotopical generalization of Deligne’s cohomological proper descent, using Lurie’s proper descent. The fact that the Chern character descends to topological K-theory is established by using Kassel’s Künneth formula for periodic cyclic homology and the proper descent. In the case of a dg-category of perfect complexes on a separated scheme of finite type, we show that we recover the usual topological K-theory of complex points. We show as well that the Chern map tensorized with 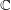 $\mathbb{C}$ is an equivalence in the case of a finite-dimensional associative algebra – providing a formula for the periodic homology groups in terms of the stack of finite-dimensional modules.
$\mathbb{C}$ is an equivalence in the case of a finite-dimensional associative algebra – providing a formula for the periodic homology groups in terms of the stack of finite-dimensional modules.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author 2015
References
- 34
- Cited by

