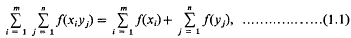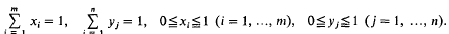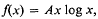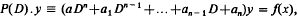Refine listing
Actions for selected content:
Contents
Research Article
Linkages for the Trisection of an Angle and Duplication of the Cube
-
- Published online by Cambridge University Press:
- 21 January 2009, pp. 1-4
-
- Article
-
- You have access
- Export citation
An Alternative Proof of a Theorem on the Lebesgue Integral
-
- Published online by Cambridge University Press:
- 21 January 2009, pp. 5-6
-
- Article
-
- You have access
- Export citation
On a Functional Equation
-
- Published online by Cambridge University Press:
- 21 January 2009, pp. 7-8
-
- Article
-
- You have access
- Export citation
Plane Collineations
-
- Published online by Cambridge University Press:
- 21 January 2009, pp. 9-11
-
- Article
-
- You have access
- Export citation
Linear Ordinary Differential Equations with Constant Coefficients: Identification of Boole's Integral with that of Cauchy
-
- Published online by Cambridge University Press:
- 21 January 2009, pp. 13-15
-
- Article
-
- You have access
- Export citation
Some Properties of the Zeros of Bessel Functions
-
- Published online by Cambridge University Press:
- 21 January 2009, pp. 17-18
-
- Article
-
- You have access
- Export citation
Obituary
Sheila Scott Macintyre
-
- Published online by Cambridge University Press:
- 21 January 2009, p. 19
-
- Article
-
- You have access
- Export citation