1. Introduction
According to a report issued by KPMG (2017), the majority (67 per cent) of firms belonging to the G250 Fortune Index – a list of the largest 250 multinationals – has revealed targets to cut carbon emissions.Footnote 1 These companies are generally characterised by the separation between ownership and control, which is delegated to managers. However, on the one hand, only 25 per cent of them link their own targets to climate goals that have been fixed by national governments, regional authorities or the United Nations, such as The Paris Agreement. On the other hand, family firms constitute another pillar of the production sector in several European, Asian and Latin American countries (see García-Ramos and García-Olalla, Reference García-Ramos and García-Olalla2011; Chrisman et al., Reference Chrisman, Memili and Misra2014; Singal and Gerde, Reference Singal and Gerde2015). In this case, the family group crucially affects the ownership, governance, management, and objectives and strategies of the firm. Regardless of their nature of public listed/privately held companies, empirical works have highlighted that family firms widely report environmental disclosure and might focus more on environmental performance than non-family businesses (Berrone et al., Reference Berrone, Cruz, Gomez-Mejia and Larraza-Kintana2010; Dekker and Hasso, Reference Dekker and Hasso2016; Arena and Michelon, Reference Arena and Michelon2018; Zhu and Lu, Reference Zhu and Lu2020). This suggests the opportunity for intervention to readjust the firms' targets in line with those of environmentally responsive social planners.
At this point, the following questions arise. In strategic settings such as oligopolistic (duopolistic) markets, is it advantageous for owners to include an incentive based on emissions (instead of sales) within a managerial scheme when the existing dirty technology causes pollution externalities? Which are the effects of this contract on environmental quality? What kind of delegation contract endogenously emerges in a game-theoretic context?
Our contribution focuses precisely on these points. To address these questions, the article concentrates on the managerial delegation theory framed in strategic competitive markets and introduces a contract based on a combination of profits and emissions instead of profits and sales, as instead was done by the pioneering works of Vickers (Reference Vickers1985), Sklivas (Reference Sklivas1987), and Fershtman and Judd (Reference Fershtman and Judd1987). Though this contract incentivises managers for emissions, we define it in a conventional way as ‘green’ delegation (GD).Footnote 2
Indeed, although the GD contract proposed in this article may apparently work in an anti-ecological direction, incentivising the manager to increase employment and production (beyond the corresponding values under SD) and reduce abatement (below the corresponding values under SD) at the pre-tax stage, it allows us to obtain eco-friendly results at equilibrium (reducing total emissions and environmental damage). This is because, by producing more and abating less than the SD manager, the optimal emissions tax levied by the government under GD to incentivise firms' emissions-reduction actions is larger than the optimal emissions tax under SD, in turn allowing the GD manager at the post-tax stage to reduce employment, production, aggregate emissions and environmental damage below the corresponding values under SD, eventually acting as the main driving force of the results. This is the essence for defining our contract based on emissions as GD. However, this transfer of resources from firms to government reduces social welfare compared to the SD scenario, thereby revealing a clear trade-off between employment (production) and welfare.
The main features of the GD contract are as follows: the ex-ante (pre-tax stage) amount of output production is larger and pollution abatement lower than the corresponding ex-ante (pre-tax stage) values under the SD delegation with abatement. However, after government intervention through the setting of an optimal emissions tax, the GD contract allows the ex-post (post-tax stage) amount of output production to be lower and pollution abatement larger than under the SD delegation with abatement. This eventually leads the GD scenario to decrease (at the equilibrium) aggregate emissions and environmental damage below the corresponding values under the SD scenario.
Public apprehension has grown worldwide due to climate scientists' emphasis on the immediate need to reduce greenhouse gases emissions because of their potential future impacts on local and global political institutions and economic systems (see ‘The climate issue’ (The Economist, 2019) and the special report on business and climate change ‘The great disrupter’ (The Economist, 2020)). Therefore, this investigation appears to be well-timed, and the subject is surprisingly absent in the industrial economics literature framed in strategic competitive contexts, apart from the work of Poyago-Theotoky and Yong (Reference Poyago-Theotoky and Yong2019) which the present work relates to. In this regard, our contribution considers a Cournot duopoly in which a dirty technology generates pollution externalities and studies the owners' decision regarding whether to delegate the choice of pollution abatement to managers when the government levies an emissions tax to incentivise firms undertaking emissions-reduction actions.
To conduct the analysis, we make use of a non-cooperative three-stage (logical timing) game augmented by a pre-play stage. At stage zero (pre-play stage or contract stage), the owner of each firm compares the nature of the contracts by choosing whether to become a delegated (‘green’ or sales) firm or a profit-maximiser under abatement. At stage one (the government stage), the government chooses the optimal emissions tax to maximise social welfare. At stage two (the bonus stage), owners choose the executive remuneration. At stage three (the market stage), either owners simultaneously choose the optimal levels of output and abatement or delegate them to managers designing a standard SD contract or a delegation contract based on emissions.
In this context, the article studies and compares three different games, always considering a firm's abatement activity and a government's activity through emissions taxes to incentivise firms' emissions-reduction actions: (1) GD versus profit maximisation (PM); (2) SD versus PM; (3) GD versus SD. If products are homogeneous, the GD contract emerges as the unique pure-strategy Pareto inefficient Nash equilibrium (‘green’ prisoner's dilemma) of the game GD versus PM (the ‘green’ delegation game) if the public awareness towards environmental quality is sufficiently high (a self-interest/mutual benefit conflict exists to become a ‘green’-delegated firm). Otherwise, if the public awareness toward environmental quality is sufficiently low, owners are engaged in a coordination game with two symmetric equilibria: firms are either GD or PM, but the PM payoff dominates GD (the ‘green’ coordination game). If products are heterogeneous (horizontal differentiation; see online appendix C), a richer range of Nash equilibria emerges in the GD game depending on the degree of public awareness toward the environmental quality (or, alternatively, against the damage caused by industrial production) coming from the environmental damage function.
Additionally, the work shows that the SD strategy under abatement emerges as the unique pure-strategy Nash equilibrium of the game SD versus PM if products are homogeneous (confirming the results of the managerial delegation literature – that is, Vickers (Reference Vickers1985), Sklivas (Reference Sklivas1987) and Fershtman and Judd (Reference Fershtman and Judd1987) – while showing the emergence of alternative Nash equilibrium outcomes if products are differentiated (in line with Fanti et al., Reference Fanti, Gori and Sodini2017a, Reference Fanti, Gori and Sodini2017b).
Finally, the comparison of the ‘green’ contract based on emissions and the sales contract under abatement reveals that the latter always emerges as the unique pure-strategy Nash equilibrium of the game that can be Pareto inefficient or Pareto efficient depending on the degree of product differentiation.
To sum up, in the ‘green’ delegation game a self-interest/mutual benefit conflict exists to become a ‘green’-delegated firm or, alternatively, a ‘green’ coordination game can emerge depending on the public awareness regarding environmental quality. However, the environmental damage is the same under GD and PM because the difference between the optimal emissions tax rate under GD and the optimal emissions tax rate under PM is exactly equal to the incentive designed by the owner about the emissions chosen by the manager who is remunerated through an incentive based on emissions. In contrast, in the games in which owners choose whether to delegate under SD versus GD or PM, the SD contract always emerges as the unique pure-strategy Pareto-inefficient Nash equilibrium. However, both the environmental damage and social welfare under SD are larger than the corresponding values under GD or PM. Therefore, comparing SD and GD reveals a clear trade-off between employment (production) and social welfare. These findings suggest that designing a managerial contract based on emissions instead of sales paradoxically favours environmental quality.
The remainder of the paper is organised as follows. Section 2 reviews the related literature. Section 3 describes the main ingredients of the Cournot duopoly with homogeneous products. Section 4 introduces the GD game, comparing the owners' endogenous choice of GD or PM. Section 5 considers the SD game by comparing SD and PM under pollution abatement. Section 6 compares GD and SD. Section 7 summarizes and concludes the paper with an outline of the future research agenda on this issue. The supplementary material online includes: (i) the welfare analysis, (ii) analytical details (appendices A and B), and (iii) an extension of the basic model with horizontal product differentiation (appendix C).
2. Literature review
The work relates to a broad corpus of the economics literature focusing on environmental issues. The first contributions made use of simple frameworks in which each firm produces homogeneous goods at a single production plant (see, amongst others, Simpson, Reference Simpson1995; Katsoulacos and Xepapadeas, Reference Katsoulacos, Xepapadeas, Carraro, Katsoulacos and Xepapadeas1996; Carlsson, Reference Carlsson2000). Then, the literature developed further by considering different market configurations. A first line of investigation in this regard studied the strategic environmental policy in an international framework by investigating how countries strategically act when the regulator levies environmental taxes, unilaterally or cooperatively. A ground-breaking contribution in this direction is Ulph (Reference Ulph1996), who considered the strategic environmental policy in countries involved in international trade and whose markets are characterised by imperfect competition.Footnote 3
A second line of research focuses on the strategic interaction between environmental policy and the endogenous location of polluting firms (e.g., Markusen et al., Reference Markusen, Morey and Olewiler1993; Rauscher, Reference Rauscher1995; Markusen, Reference Markusen1997; Bárcena-Ruiz and Garzón, Reference Bárcena-Ruiz and Garzón2003), whereas another branch investigates the link between environmental policies and market structures (Lee, Reference Lee1975, Reference Lee1999; Smith, Reference Smith1976; Oates and Strassmann, Reference Oates and Strassmann1984; Conrad and Wang, Reference Conrad and Wang1993; Katsoulacos and Xepapadeas, Reference Katsoulacos, Xepapadeas, Carraro, Katsoulacos and Xepapadeas1996; Althammer and Bucholz, Reference Althammer and Bucholz1999; Cato, Reference Cato2010). Another strand of research also investigates the relationship between vertical structures in an industry (e.g., supply chains) and environmental taxes (Sheu, Reference Sheu2011; Gunasekaran et al., Reference Gunasekaran, Subramanian and Rahman2015; Park et al., Reference Park, Cachon, Lai and Seshadri2015; Hafezalkotob, Reference Hafezalkotob2017; Bian et al., Reference Bian, Guo and Li2018).
Other works analysed and extended the basic framework of oligopolistic rivalry by assuming either unionised oligopolies (Bárcena-Ruiz and Garzón, Reference Bárcena-Ruiz and Garzón2003, Reference Bárcena-Ruiz and Garzón2009; Bárcena-Ruiz, Reference Bárcena-Ruiz2011) or (as our paper does) the separation between ownership and control by introducing managerial delegation contracts. The pioneering work of Bárcena-Ruiz and Garzón (Reference Bárcena-Ruiz and Garzón2002) studied the strategic effects of delegating to managers a firm's sales and pollution abatement in the presence of environmental tax and damage by considering a competitive labour market and homogeneous products.
Bárcena-Ruiz and Garzón (Reference Bárcena-Ruiz and Garzón2003) also studied a managerial delegation model in a framework in which the government sets an environmental tax to control environmental damage. The authors showed that, by offering managers a standard incentive scheme based on a linear combination of profits and sales revenue, on the one hand, firms' owners get profits lower than under standard PM; on the other hand, they must pay a higher environmental tax and both the environmental damage and social welfare with managerial delegation increase.
Subsequently, Pal (Reference Pal2012) extended the work of Bárcena-Ruiz and Garzón (Reference Bárcena-Ruiz and Garzón2002) by examining the impact of strategic managerial delegation, product differentiation, and alternative modes of market (price and quantity) competition on the optimal emissions tax rate, environmental damage and social welfare. The author showed that, under the standard PM rule, the optimal emissions tax does not inevitably decrease with the degree of differentiation among products. Moreover, if managers receive a standard remuneration scheme consisting of a linear combination of profits and sales revenues, the impacts of delegation on the scope for the optimal emissions tax are lower for the higher degree of product differentiation; these impacts are significantly different under alternative modes of competition. Under price (resp. quantity) competition, profits in the case of managerial delegation are higher (resp. lower) than without delegation, but the opposite holds true for equilibrium emissions tax rate, environmental damage and social welfare.
There also exists a recent line of research that considers the idea of ‘green’ managerial delegation, that is, the introduction of an environmental incentive into the managerial compensation scheme. The present article especially contributes to this literature. Lee and Park (Reference Lee and Park2019) were the first authors to include an explicit environmental incentive in a managerial compensation contract, representing a form of environmental corporate social responsibility (ECSR). In a sequential price competition game, the authors study the strategic choice of adopting ECSR among polluting firms. The measure of ECSR is given using the internal emission price on the damage produced by the firm, as established by the firm's owners. The managerial compensation structure is a linear combination of profits and the ECSR incentive. In such a context, the main result is that, when firms sequentially adopt ECSR, they do so to soften competition when the goods are close substitutes; nonetheless, the late adopter selects a lower level of ECSR than the early one, and thus earns higher profit. In a Cournot duopoly with pollution externalities and emissions taxes, Poyago-Theotoky and Yong (Reference Poyago-Theotoky and Yong2019) also introduced an explicit environmental incentive into the compensation scheme that owners offer their managers (environmental delegation), thereby designing a contract based on a linear combination of profits and tax savings, where the latter component has the aim of rewarding the manager for pollution abatement to reduce the firm's emissions tax bill. The authors showed that, depending on the efficiency level of the ‘green’ research and development activity, the environmental delegation contract yields greater abatement levels than the standard revenue delegation contract, as in Fershtman and Judd (Reference Fershtman and Judd1987). Consequently, the regulator fixes a lower emissions tax, and social welfare increases. In addition, firm owners earn higher profits when adopting the environmental delegation contract than the revenue delegation contract with pollution abatement.
However, despite the different aspects and contexts studied, none of these contributions (including Poyago-Theotoky and Yong (Reference Poyago-Theotoky and Yong2019)) has incorporated into the analysis the firm's endogenous choice to adopt an abatement technology when the government selects an optimal environmental tax, as the present paper does.
3. The model with homogeneous products
Consider a duopoly industry in which firm 1 and firm 2 compete in a Cournot rivalry setting by producing quantities ${q_1}$![]() and ${q_2}$
and ${q_2}$![]() , respectively, whose varieties are perceived as homogeneous. The existing technology allows firm i $(i = 1,2)$
, respectively, whose varieties are perceived as homogeneous. The existing technology allows firm i $(i = 1,2)$![]() to produce ${q_i}$
to produce ${q_i}$![]() units of output of variety i, causing ${e_i}$
units of output of variety i, causing ${e_i}$![]() units of emissions (pollution), where ${e_i} = {q_i} - {k_i}$
units of emissions (pollution), where ${e_i} = {q_i} - {k_i}$![]() (Ulph, Reference Ulph1996), with $0 \le {k_i} < {q_i}$
(Ulph, Reference Ulph1996), with $0 \le {k_i} < {q_i}$![]() representing the abatement level for environmental protection coming from a cleaning technology available to each firm, implying that emissions cannot be entirely eliminated.Footnote 4 The available technology is such that firm i produces with a constant returns to scale production function, that is, ${q_i} = {L_i}$
representing the abatement level for environmental protection coming from a cleaning technology available to each firm, implying that emissions cannot be entirely eliminated.Footnote 4 The available technology is such that firm i produces with a constant returns to scale production function, that is, ${q_i} = {L_i}$![]() , where L i represents the labour force employed by the firm and whose identical (constant) average and marginal cost is $w \ge 0$
, where L i represents the labour force employed by the firm and whose identical (constant) average and marginal cost is $w \ge 0$![]() (representing the wage per unit of labour) for every unit of output produced. Therefore, firm $i$
(representing the wage per unit of labour) for every unit of output produced. Therefore, firm $i$![]() 's cost function is ${C_i}({{q_i}} )= w{L_i} = w{q_i}$
's cost function is ${C_i}({{q_i}} )= w{L_i} = w{q_i}$![]() . In addition, the pollution abatement cost function of firm i is $C{A_i}({{k_i}} )= (z/2)k_i^2$
. In addition, the pollution abatement cost function of firm i is $C{A_i}({{k_i}} )= (z/2)k_i^2$![]() , where $z > 0$
, where $z > 0$![]() is a parameter that scales up/down the total abatement cost and represents an exogenous index of technological progress while measuring, for example, the appearance of a new, cost-effective cleaning technology. Indeed, it measures the degree to which the available technology for pollution abatement impacts the environment. A reduction in z can be interpreted as an improvement in the technological progress in abatement so that abating becomes cheaper. The adoption of a clean technology requires sustaining costs with decreasing returns on investment. This implies that, when firms choose to abate emissions, they always face some costs. One might consider a cleaning technology not directly linked to output, for example, ‘the number of the filters in a refinery's pipe for CO2 reduction or ‘scrubbers’ to remove SO2 from a fuel gas coal fired electric plant’ (Asproudis and Gil-Moltó, Reference Asproudis and Gil-Moltó2015: 169). As ${k_i}$
is a parameter that scales up/down the total abatement cost and represents an exogenous index of technological progress while measuring, for example, the appearance of a new, cost-effective cleaning technology. Indeed, it measures the degree to which the available technology for pollution abatement impacts the environment. A reduction in z can be interpreted as an improvement in the technological progress in abatement so that abating becomes cheaper. The adoption of a clean technology requires sustaining costs with decreasing returns on investment. This implies that, when firms choose to abate emissions, they always face some costs. One might consider a cleaning technology not directly linked to output, for example, ‘the number of the filters in a refinery's pipe for CO2 reduction or ‘scrubbers’ to remove SO2 from a fuel gas coal fired electric plant’ (Asproudis and Gil-Moltó, Reference Asproudis and Gil-Moltó2015: 169). As ${k_i}$![]() represents the pollutant abated per ${q_i}$
represents the pollutant abated per ${q_i}$![]() units of output, a larger (resp. smaller) value of ${k_i}$
units of output, a larger (resp. smaller) value of ${k_i}$![]() corresponds ceteris paribus to a more (resp. less) efficient abatement. To preserve analytical tractability and without loss of generality, we set $z = 1$
corresponds ceteris paribus to a more (resp. less) efficient abatement. To preserve analytical tractability and without loss of generality, we set $z = 1$![]() henceforth.Footnote 5 Industrial production causes environmental damage measured by the index ${\rm ED} = (g/2){({e_1} + {e_2})^2}$
henceforth.Footnote 5 Industrial production causes environmental damage measured by the index ${\rm ED} = (g/2){({e_1} + {e_2})^2}$![]() , where $g > 0$
, where $g > 0$![]() is the burden the government attaches to the environmental damage, representing the awareness of the overall society towards a clean environment, and thus against the severe or mild environmental damages generated by industrial production, and the sum ${e_1} + {e_2}$
is the burden the government attaches to the environmental damage, representing the awareness of the overall society towards a clean environment, and thus against the severe or mild environmental damages generated by industrial production, and the sum ${e_1} + {e_2}$![]() represents aggregate emissions. An increase in g implies ceteris paribus an increase in the extent of the relative weight of the environmental damage as measured by the government, implying that the overall society is more aware of environmental protection. This type of damage function is commonly used in the related literature and assumes that: (i) the environmental damage is a convex function of total pollution, and (ii) the damage is exogenous for consumers; see, for example, van der Ploeg and de Zeeuw (Reference van der Ploeg and de Zeeuw1992) and Ulph (Reference Ulph1996). The objective function of the profit-maximising firm i is given by ${\pi _i}$
represents aggregate emissions. An increase in g implies ceteris paribus an increase in the extent of the relative weight of the environmental damage as measured by the government, implying that the overall society is more aware of environmental protection. This type of damage function is commonly used in the related literature and assumes that: (i) the environmental damage is a convex function of total pollution, and (ii) the damage is exogenous for consumers; see, for example, van der Ploeg and de Zeeuw (Reference van der Ploeg and de Zeeuw1992) and Ulph (Reference Ulph1996). The objective function of the profit-maximising firm i is given by ${\pi _i}$![]() (profits). Differently, if the owner of firm i delegates production and abatement decisions to a manager, the objective function of manager i is given by ${U_i}$
(profits). Differently, if the owner of firm i delegates production and abatement decisions to a manager, the objective function of manager i is given by ${U_i}$![]() (manager's utility). Both the profit function and manager's utility function will be specified later in this article.
(manager's utility). Both the profit function and manager's utility function will be specified later in this article.
We assume a linear (inverse) market demand given by $p = \alpha - \beta Q$![]() , where $\alpha$
, where $\alpha$![]() is a positive parameter representing the market size $(\alpha > w \ge 0),\;\beta > 0$
is a positive parameter representing the market size $(\alpha > w \ge 0),\;\beta > 0$![]() measures the slope of the market demand being part of its elasticity, and $Q = {q_1} + {q_2}$
measures the slope of the market demand being part of its elasticity, and $Q = {q_1} + {q_2}$![]() is total supply.Footnote 6 This kind of demand structure comes from the usual specification of quadratic utility for consumers' preferences, that is $V({{q_1},{q_2}} )= \alpha ({{q_1} + {q_2}} )- (\beta /2){({q_1} + \; {q_2})^2}$
is total supply.Footnote 6 This kind of demand structure comes from the usual specification of quadratic utility for consumers' preferences, that is $V({{q_1},{q_2}} )= \alpha ({{q_1} + {q_2}} )- (\beta /2){({q_1} + \; {q_2})^2}$![]() , as proposed by Dixit (Reference Dixit1979) and subsequently used by, amongst others, Singh and Vives (Reference Singh and Vives1984). To maintain analytical tractability (and without loss of generality), we assume $\alpha = 1,\;\beta = 1$
, as proposed by Dixit (Reference Dixit1979) and subsequently used by, amongst others, Singh and Vives (Reference Singh and Vives1984). To maintain analytical tractability (and without loss of generality), we assume $\alpha = 1,\;\beta = 1$![]() , and $w = 0$
, and $w = 0$![]() henceforth.
henceforth.
The government levies an emissions tax $t \in ({0,1} ]$![]() per each unit of polluting output to incentivise firms undertaking emissions-reduction actions with the aim of maximising social welfare.Footnote 7 Consequently, the tax base of firm i is ${q_i} - {k_i}$
per each unit of polluting output to incentivise firms undertaking emissions-reduction actions with the aim of maximising social welfare.Footnote 7 Consequently, the tax base of firm i is ${q_i} - {k_i}$![]() (i.e., the remaining pollution after abatement), and the corresponding tax revenue is $t({{q_i} - {k_i}} )$
(i.e., the remaining pollution after abatement), and the corresponding tax revenue is $t({{q_i} - {k_i}} )$![]() .
.
Definitively, our non-cooperative game has a three-stage (logical timing) structure augmented by a pre-play stage (see the introduction for details), as depicted in figure 1.

Figure 1. Logical timing of the game.
4. ‘Green’ delegation (GD) versus profit maximisation (PM) with homogeneous products
4.1 The symmetric subgame PM/PM
Consider first the subgame in which the decision about industrial production and abatement is taken by the owner of each firm (i.e., firms are profit maximisers) at the market stage of the game, i.e., the PM scheme works as if the bonus set by the owner to the manager were equal to zero. The profit function of firm i is:
At the market stage of the game, owners choose both the optimal amount of output coming from industrial production and abatement to maximise profits. Maximisation of equation (1) with respect to ${q_i}$![]() and ${k_i}$
and ${k_i}$![]() yields the following set of first-order conditions:
yields the following set of first-order conditions:
where the superscript PM/PM stands for profit maximisation of both firms. The solution of the system of output reaction functions $\bar{q}_i^{{\rm PM/PM}}\;(i = 1,2,\;i \ne j)$![]() in equation (2) leads firm i to produce the following pre-tax stage equilibrium quantity of product of variety i as a function of the emissions tax $t.$
in equation (2) leads firm i to produce the following pre-tax stage equilibrium quantity of product of variety i as a function of the emissions tax $t.$![]() That is,
That is,
Using equation (3) and the first-order condition $k_i^{{\rm PM/PM}} = t$![]() in equation (2), one can directly obtain the equilibrium expressions for the producer surplus $({\rm P}{{\rm S}^{{\rm PM/PM}}})$
in equation (2), one can directly obtain the equilibrium expressions for the producer surplus $({\rm P}{{\rm S}^{{\rm PM/PM}}})$![]() , consumer surplus $({\rm C}{{\rm S}^{{\rm PM/PM}}})$
, consumer surplus $({\rm C}{{\rm S}^{{\rm PM/PM}}})$![]() , tax revenues $({\rm T}{{\rm R}^{{\rm PM/PM}}})$
, tax revenues $({\rm T}{{\rm R}^{{\rm PM/PM}}})$![]() and environmental damage $({\rm E}{{\rm D}^{{\rm PM/PM}}})$
and environmental damage $({\rm E}{{\rm D}^{{\rm PM/PM}}})$![]() as a function of the tax rate when both firms are profit maximisers (reported in online appendix B), allowing us to obtain social welfare under PM/PM $({\rm S}{{\rm W}^{{\rm PM/PM}}} = {\rm P}{{\rm S}^{{\rm PM/PM}}} + {\rm C}{{\rm S}^{{\rm PM/PM}}} + {\rm T}{{\rm R}^{{\rm PM/PM}}} - {\rm E}{{\rm D}^{{\rm PM/PM}}})$
as a function of the tax rate when both firms are profit maximisers (reported in online appendix B), allowing us to obtain social welfare under PM/PM $({\rm S}{{\rm W}^{{\rm PM/PM}}} = {\rm P}{{\rm S}^{{\rm PM/PM}}} + {\rm C}{{\rm S}^{{\rm PM/PM}}} + {\rm T}{{\rm R}^{{\rm PM/PM}}} - {\rm E}{{\rm D}^{{\rm PM/PM}}})$![]() , which is reported in lemma 1.
, which is reported in lemma 1.
Lemma 1 The social welfare function under PM/PM as a function of the tax rate is given by:
At the first stage of the subgame (the government stage), the government levies an emissions tax with the aim of maximising social welfare. Proposition 1 shows the extent of the welfare maximising tax rate ${t^{{\ast {\rm PM/PM}}}}$![]() and the condition under which the optimal tax rate in the subgame PM/PM is positive (see proofs of lemma 1 and proposition 1 in online appendix B).
and the condition under which the optimal tax rate in the subgame PM/PM is positive (see proofs of lemma 1 and proposition 1 in online appendix B).
Proposition 1 The welfare-maximising tax rate under PM/PM is given by the following expression, which is positive if and only if $g > 0.125$![]() :
:
Using the optimal tax rate in equation (5), one obtains the equilibrium quantities of industrial production $q_i^{\mathrm{\ast PM/PM}} = (4(2g + 1)/(32g + 11)) > 0$![]() , abatement $k_i^{\mathrm{\ast PM/PM}} = ((8g - 1)/(32g + 11)) > 0\;g > 0.125$
, abatement $k_i^{\mathrm{\ast PM/PM}} = ((8g - 1)/(32g + 11)) > 0\;g > 0.125$![]() , and emissions $q_i^{\mathrm{\ast PM/PM}} - k_i^{\mathrm{\ast PM/PM}} > 0$
, and emissions $q_i^{\mathrm{\ast PM/PM}} - k_i^{\mathrm{\ast PM/PM}} > 0$![]() . Finally, inserting back the optimal tax ${t^{\mathrm{\ast PM/PM}}}$
. Finally, inserting back the optimal tax ${t^{\mathrm{\ast PM/PM}}}$![]() into the profit function in equation (1), one gets equilibrium profits under PM/PM, that is:
into the profit function in equation (1), one gets equilibrium profits under PM/PM, that is:
4.2. The symmetric subgame GD/GD
Let us now consider the case in which owners delegate output and abatement decisions to their own managers by designing a delegation contract that includes an environmental component based on emissions (GD), i.e., firms are ‘green’ delegated at the market stage of the game. In a managerial delegation model framed in a strategic competitive context, each firm consists of owners who control the firm and a manager whose decisions are based on an incentive contract that the corresponding owner designs. Managers get a publicly observed contract whose remuneration is ${R_i} = \mathrm{{\rm A}} + \mathrm{{\rm B}}{U_i} \ge 0$![]() , where $\mathrm{{\rm A}} \ge 0$
, where $\mathrm{{\rm A}} \ge 0$![]() is the fixed salary component of the manager's compensation, $\mathrm{{\rm B}} \ge 0$
is the fixed salary component of the manager's compensation, $\mathrm{{\rm B}} \ge 0$![]() is a constant parameter, and ${U_i}$
is a constant parameter, and ${U_i}$![]() is the manager $i$
is the manager $i$![]() 's utility. Without loss of generality, we set $\mathrm{{\rm A}} = 0$
's utility. Without loss of generality, we set $\mathrm{{\rm A}} = 0$![]() and $\mathrm{{\rm B}} = 1$
and $\mathrm{{\rm B}} = 1$![]() henceforth. Each manager's compensation structure is proportional to a linear combination of profit and an incentive based on emissions. The objective function of the manager of the polluting firm i takes a form like those introduced by Vickers (Reference Vickers1985), Sklivas (Reference Sklivas1987), and Fershtman and Judd (Reference Fershtman and Judd1987) in their pioneering contributions. The equation is:
henceforth. Each manager's compensation structure is proportional to a linear combination of profit and an incentive based on emissions. The objective function of the manager of the polluting firm i takes a form like those introduced by Vickers (Reference Vickers1985), Sklivas (Reference Sklivas1987), and Fershtman and Judd (Reference Fershtman and Judd1987) in their pioneering contributions. The equation is:
weighting profits and emissions instead of profits and sales. In equation (7), ${\pi _i}$![]() is the profit function defined in equation (1), and ${b_i} > 0\; ( < 0)$
is the profit function defined in equation (1), and ${b_i} > 0\; ( < 0)$![]() is the incentive (disincentive) designed by the owner regarding quantity and abatement (i.e., emissions) chosen by the manager, which determines actual pollution of firm i, that is, ${e_i} = {q_i} - {k_i}$
is the incentive (disincentive) designed by the owner regarding quantity and abatement (i.e., emissions) chosen by the manager, which determines actual pollution of firm i, that is, ${e_i} = {q_i} - {k_i}$![]() . Therefore, the maximisation of the utility function in equation (7) by manager i with respect to ${q_i}$
. Therefore, the maximisation of the utility function in equation (7) by manager i with respect to ${q_i}$![]() and ${k_i}$
and ${k_i}$![]() at the market stage of the subgame leads to the following set of first-order conditions:Footnote 8
at the market stage of the subgame leads to the following set of first-order conditions:Footnote 8
where the superscript GD/GD stands for the ‘green’ delegation of both managers. The solution of the system of output reaction functions $\bar{q}_i^{{\rm GD/GD}}$![]() $(i = 1,2,\;i \ne j)$
$(i = 1,2,\;i \ne j)$![]() in equation (8) gives the following pre-tax stage equilibrium output as a function of the emissions tax t and the bonuses ${b_i}$
in equation (8) gives the following pre-tax stage equilibrium output as a function of the emissions tax t and the bonuses ${b_i}$![]() and ${b_j}$
and ${b_j}$![]() . That is:
. That is:
A direct comparison between equations (2) and (8) reveals that the ‘green’ contract promotes industrial production (as expected) and reduces abatement due to the design of the executive remuneration at the bonus stage (based on emissions instead of sales), apparently working at first glance as an anti-ecological device at the pre-tax stage compared to the case of profit maximisation $({b_i} = 0)$![]() .
.
However, this section will show that the design of the GD contract by the owner allowing the ‘green’ manager to produce more and abate less than the owner under the PM contract, is such that the welfare-maximising emissions tax levied by the government at the government stage under GD goes beyond the corresponding value under PM. This eventually implies that equilibrium production and abatement at the post-tax stage of the game under GD are the same as equilibrium production and abatement at the post-tax stage of the game under PM,Footnote 9 allowing the same level of aggregate emissions and environmental damage to be achieved.
This policy-driven mechanism – based on a transfer of resources flowing from firms to the public authority – allows the government to perfectly compensate the increased emissions with a larger ad hoc taxation that lowers production and increases abatement under GD. Indeed, the difference between the optimal emissions tax rate under GD and the optimal emissions tax rate under PM is exactly equal to the incentive designed by the owner about the emissions chosen by the manager who is remunerated through an incentive based on emissions. This implies that the GD contract is not anti-ecological compared to the PM contract and there is no trade-off between employment (production) and social welfare in this case (see the welfare analysis in the online appendix for a thoughtful discussion of this issue).
A relevant effect of the emissions tax is to increase marginal costs and reduce equilibrium profits of the GD strategy below the equilibrium profit of the PM strategy. The former, however, will become a dominant strategy so that (GD, GD) will be the Pareto inefficient Nash equilibrium of the GD game if the public awareness towards environmental quality is high enough. Note that we are considering total pollution and the corresponding environmental damage as the main indexes to evaluate the ‘greenness’ of a managerial contract. Thus, the GD contract reduces both below the corresponding values obtained through the SD contract under abatement (see the welfare analysis in the online appendix for a thoughtful discussion of the post-tax equilibrium values of environmental damage, emissions tax, consumer's surplus, profits and social welfare under SD/SD, GD/GD and PM/PM).
Substituting equation (9) and $k_i^{{\rm GD/GD}} = t - {b_i}$![]() in equation (8) into the profit function in equation (1) allows us to get the expression of firm $i$
in equation (8) into the profit function in equation (1) allows us to get the expression of firm $i$![]() 's profit as a function of the managerial incentives ${b_i}$
's profit as a function of the managerial incentives ${b_i}$![]() and ${b_j}$
and ${b_j}$![]() . Therefore, at the bonus stage owner i maximises profits with respect to ${b_i}$
. Therefore, at the bonus stage owner i maximises profits with respect to ${b_i}$![]() , which leads to the following reaction functions in the bonus space:
, which leads to the following reaction functions in the bonus space:
From equation (10), it is clear that ${b_i}$![]() and ${b_j}$
and ${b_j}$![]() are strategic substitutes,Footnote 10 i.e., an increase in executive remuneration in firm j reduces executive remuneration in firm i, and the symmetric equilibrium values of both bonus and abatement of player i as a function of the tax rate are:
are strategic substitutes,Footnote 10 i.e., an increase in executive remuneration in firm j reduces executive remuneration in firm i, and the symmetric equilibrium values of both bonus and abatement of player i as a function of the tax rate are:
Making use of equation (11), further substitutions directly yield the equilibrium expressions for the producer surplus $({\rm P}{{\rm S}^{{\rm GD/GD}}})$![]() , consumer surplus $({\rm C}{{\rm S}^{{\rm GD/GD}}})$
, consumer surplus $({\rm C}{{\rm S}^{{\rm GD/GD}}})$![]() , tax revenues $({\rm T}{{\rm R}^{{\rm GD/GD}}})$
, tax revenues $({\rm T}{{\rm R}^{{\rm GD/GD}}})$![]() , and environmental damage $({\rm E}{{\rm D}^{{\rm GD/GD}}})$
, and environmental damage $({\rm E}{{\rm D}^{{\rm GD/GD}}})$![]() as a function of the tax rate when both firms are ‘green’ delegated (reported in online appendix B), allowing us to get social welfare under GD/GD $({\rm S}{{\rm W}^{{\rm GD/GD}}} = {\rm P}{{\rm S}^{{\rm GD/GD}}} + {\rm C}{{\rm S}^{{\rm GD/GD}}} + {\rm T}{{\rm R}^{{\rm GD/GD}}} - {\rm E}{{\rm D}^{{\rm GD/GD}}})$
as a function of the tax rate when both firms are ‘green’ delegated (reported in online appendix B), allowing us to get social welfare under GD/GD $({\rm S}{{\rm W}^{{\rm GD/GD}}} = {\rm P}{{\rm S}^{{\rm GD/GD}}} + {\rm C}{{\rm S}^{{\rm GD/GD}}} + {\rm T}{{\rm R}^{{\rm GD/GD}}} - {\rm E}{{\rm D}^{{\rm GD/GD}}})$![]() , which is reported in lemma 2.
, which is reported in lemma 2.
Lemma 2 The social welfare function under GD/GD as a function of the tax rate is given by:
At the first stage of the subgame, the government levies an emissions tax with the aim of maximising social welfare. Proposition 2 shows the extent of the welfare-maximising tax rate ${{t}^{{\ast} {\rm GD}/{\rm GD}}}$![]() and the condition under which the optimal tax rate in the subgame GD/GD is positive (see proofs of lemma 2 and proposition 2 in online appendix B).
and the condition under which the optimal tax rate in the subgame GD/GD is positive (see proofs of lemma 2 and proposition 2 in online appendix B).
Proposition 2 The welfare-maximising tax rate under GD/GD is given by the following expression, which is positive if and only if $g > 0.020833$![]() :
:
Using the optimal tax rate in equation (13), one obtains the equilibrium quantities of industrial production $q_i^{\mathrm{\ast GD/GD}} = (4(2g + 1)/(32g + 11)) > 0$![]() , executive remuneration $b_i^{\mathrm{\ast GD/GD}} = (4(2g + 1)/(5(32g + 11))) > 0$
, executive remuneration $b_i^{\mathrm{\ast GD/GD}} = (4(2g + 1)/(5(32g + 11))) > 0$![]() , abatement $k_i^{\mathrm{\ast GD/GD}} = ((8g - 1)/(32g + 11)) > 0$
, abatement $k_i^{\mathrm{\ast GD/GD}} = ((8g - 1)/(32g + 11)) > 0$![]() for any $g > 0.020833$
for any $g > 0.020833$![]() , and emissions $q_i^{\mathrm{\ast GD/GD}} - k_i^{\mathrm{\ast GD/GD}} > 0$
, and emissions $q_i^{\mathrm{\ast GD/GD}} - k_i^{\mathrm{\ast GD/GD}} > 0$![]() . Finally, inserting back the optimal tax ${t^{\mathrm{\ast GD/GD}}}$
. Finally, inserting back the optimal tax ${t^{\mathrm{\ast GD/GD}}}$![]() into the profit function in equation (1), one gets equilibrium profits under GD/GD. That is:
into the profit function in equation (1), one gets equilibrium profits under GD/GD. That is:
A direct comparison amongst the relevant equations of the subgames PM/PM and GD/GD allows us to conclude that $\pi _i^{\mathrm{\ast GD/GD}} < \pi _i^{\mathrm{\ast PM/PM}}$![]() , whereas the post-tax equilibrium amount of industrial production and abatement are identical in both cases. Indeed, though the ‘green’ manager chooses to abate a smaller amount of pollution in comparison to the profit maximising firm, the pre-tax output under GD/GD is larger than the pre-tax output under PM/PM due to the design of the incentive contract through the manager's executive remuneration (bonus) chosen by the owner, so that the optimal environmental tax rate is higher under GD. Indeed, a direct comparison between equation (5) and (13) allows us to observe ${t^{\mathrm{\ast GD/GD}}} > {t^{\mathrm{\ast PM/PM}}}$
, whereas the post-tax equilibrium amount of industrial production and abatement are identical in both cases. Indeed, though the ‘green’ manager chooses to abate a smaller amount of pollution in comparison to the profit maximising firm, the pre-tax output under GD/GD is larger than the pre-tax output under PM/PM due to the design of the incentive contract through the manager's executive remuneration (bonus) chosen by the owner, so that the optimal environmental tax rate is higher under GD. Indeed, a direct comparison between equation (5) and (13) allows us to observe ${t^{\mathrm{\ast GD/GD}}} > {t^{\mathrm{\ast PM/PM}}}$![]() for any g. This implies, ceteris paribus, that the equilibrium pre-tax consumer surplus and total revenue when designing GD are larger than in the PM/PM case, thus causing the society under GD/GD to be willing to pay a larger amount of environmental taxes than under PM/PM. However, as the difference between the optimal emissions tax rate under GD/GD and the optimal emissions tax rate under PM/PM is exactly equal to the incentive designed by the owner about the emissions chosen by the manager, the post-tax equilibrium amounts of production and abatement are the same under both contracts, and profits under GD/GD are lower than profits under PM/PM as the post-tax marginal costs are larger in the former case.
for any g. This implies, ceteris paribus, that the equilibrium pre-tax consumer surplus and total revenue when designing GD are larger than in the PM/PM case, thus causing the society under GD/GD to be willing to pay a larger amount of environmental taxes than under PM/PM. However, as the difference between the optimal emissions tax rate under GD/GD and the optimal emissions tax rate under PM/PM is exactly equal to the incentive designed by the owner about the emissions chosen by the manager, the post-tax equilibrium amounts of production and abatement are the same under both contracts, and profits under GD/GD are lower than profits under PM/PM as the post-tax marginal costs are larger in the former case.
4.3 The asymmetric subgame GD/PM
To determine the owners' endogenous choice regarding whether to delegate via a ‘green’ contract based on emissions or be a profit maximiser at the pre-play stage (or contract stage), one should evaluate the outcomes of the asymmetric subgame in which one firm, say firm 1, is a ‘green’-delegated firm $({b_1} \ne 0)$![]() , and the rival, firm 2, is still profit maximising $({b_2} = 0)$
, and the rival, firm 2, is still profit maximising $({b_2} = 0)$![]() . The optimisation problems of the GD player and the PM player at the market stage provide the first-order conditions as in equation (8) for firm 1 and as in equation (2) for firm 2. Solving the system of output reaction functions, one obtains the quantities produced by both firms as a function of the tax rate and the bonus of the ‘green’ delegated firm 1. That is:
. The optimisation problems of the GD player and the PM player at the market stage provide the first-order conditions as in equation (8) for firm 1 and as in equation (2) for firm 2. Solving the system of output reaction functions, one obtains the quantities produced by both firms as a function of the tax rate and the bonus of the ‘green’ delegated firm 1. That is:
Substituting equation (15) and the expression of $k_i^{{\rm GD/GD}}$![]() in equation (8) into the profit function of firm 1, one obtains the expression of firm 1's profits as a function of the managerial incentive. At the bonus stage, the owner of firm 1 maximises profits with respect to ${b_1}$
in equation (8) into the profit function of firm 1, one obtains the expression of firm 1's profits as a function of the managerial incentive. At the bonus stage, the owner of firm 1 maximises profits with respect to ${b_1}$![]() . This gives the optimal bonus $b_1^{{\rm GD/PM}} = (1/13)({1 - t} )$
. This gives the optimal bonus $b_1^{{\rm GD/PM}} = (1/13)({1 - t} )$![]() , so that the equilibrium expressions of quantity and abatement of firm 1 and firm 2 as a function of the tax rate are:
, so that the equilibrium expressions of quantity and abatement of firm 1 and firm 2 as a function of the tax rate are:
Further substitutions by making use of equation (16) yield the equilibrium expressions for the producer surplus $({\rm P}{{\rm S}^{{\rm GD/PM}}})$![]() , consumer surplus $({\rm C}{{\rm S}^{{\rm GD/PM}}})$
, consumer surplus $({\rm C}{{\rm S}^{{\rm GD/PM}}})$![]() , tax revenues $({\rm T}{{\rm R}^{{\rm GD/PM}}})$
, tax revenues $({\rm T}{{\rm R}^{{\rm GD/PM}}})$![]() and environmental damage $({\rm E}{{\rm D}^{{\rm GD/PM}}})$
and environmental damage $({\rm E}{{\rm D}^{{\rm GD/PM}}})$![]() as a function of the tax rate when firm 1 is ‘green’ delegated and firm 2 is profit maximising (reported in online appendix B), thus providing social welfare under GD/PM $({\rm S}{{\rm W}^{{\rm GD/PM}}} = {\rm P}{{\rm S}^{{\rm GD/PM}}} + {\rm C}{{\rm S}^{{\rm GD/PM}}} + {\rm T}{{\rm R}^{{\rm GD/PM}}} - {\rm E}{{\rm D}^{{\rm GD/PM}}})$
as a function of the tax rate when firm 1 is ‘green’ delegated and firm 2 is profit maximising (reported in online appendix B), thus providing social welfare under GD/PM $({\rm S}{{\rm W}^{{\rm GD/PM}}} = {\rm P}{{\rm S}^{{\rm GD/PM}}} + {\rm C}{{\rm S}^{{\rm GD/PM}}} + {\rm T}{{\rm R}^{{\rm GD/PM}}} - {\rm E}{{\rm D}^{{\rm GD/PM}}})$![]() , reported in lemma 3.
, reported in lemma 3.
Lemma 3 The social welfare function under GD/PM as a function of the tax rate is given by:
At the first stage of the subgame, the government levies an emissions tax with the aim of maximising social welfare. Proposition 3 shows the extent of the welfare-maximising tax rate ${{t}^{{\ast} {\rm GD}/{\rm PM}}}$![]() and the condition under which the optimal tax rate in the subgame GD/PM is positive (see proofs of lemma 3 and proposition 3 in online appendix B).
and the condition under which the optimal tax rate in the subgame GD/PM is positive (see proofs of lemma 3 and proposition 3 in online appendix B).
Proposition 3 The welfare-maximising tax rate under GD/PM is given by the following expression, which is positive if and only if $g > 0.06111$![]() :
:
Using the optimal tax rate in equation (18), one obtains the equilibrium quantities of industrial production $q_1^{\ast {\rm GD}/{\rm PM}} = (90(2g + 1)/(648g + 223)) > 0,\;q_2^{\ast {\rm GD}/{\rm PM}} = ((72(2g \,{+}\, 1))/(648g \,{+}\, 223)) > 0$![]() , executive remuneration $b_1^{\ast {\rm GD}/{\rm PM}} = ((18(2g \,{+}\, 1))/ (648g + 223)) > 0$
, executive remuneration $b_1^{\ast {\rm GD}/{\rm PM}} = ((18(2g \,{+}\, 1))/ (648g + 223)) > 0$![]() , abatement $k_1^{\ast {\rm GD}/{\rm PM}} = ((144g - 29)/(648g + 223)) > 0$
, abatement $k_1^{\ast {\rm GD}/{\rm PM}} = ((144g - 29)/(648g + 223)) > 0$![]() for any $g > 0.20138, k_2^{{\ast {\rm GD}}/{\rm PM}} \,{=}\, ((180g \,{-}\, 11)/(648g \,{+}\, 223)) > 0$
for any $g > 0.20138, k_2^{{\ast {\rm GD}}/{\rm PM}} \,{=}\, ((180g \,{-}\, 11)/(648g \,{+}\, 223)) > 0$![]() for any $g > 0.06111$
for any $g > 0.06111$![]() , and emissions $q_1^{\ast {\rm GD}/{\rm PM}} - k_1^{\ast {\rm GD}/{\rm PM}} > 0$
, and emissions $q_1^{\ast {\rm GD}/{\rm PM}} - k_1^{\ast {\rm GD}/{\rm PM}} > 0$![]() and $q_2^{\ast {\rm GD}/{\rm PM}} - k_2^{\ast {\rm GD}/{\rm PM}} > 0$
and $q_2^{\ast {\rm GD}/{\rm PM}} - k_2^{\ast {\rm GD}/{\rm PM}} > 0$![]() for any $0.06111 < g < 2.305$
for any $0.06111 < g < 2.305$![]() . Finally, inserting the optimal tax ${t^{\ast {\rm GD}/{\rm PM}}}$
. Finally, inserting the optimal tax ${t^{\ast {\rm GD}/{\rm PM}}}$![]() back into the profit function in equation (1), one gets equilibrium profits under GD/PM for firm 1 and firm 2, respectively:
back into the profit function in equation (1), one gets equilibrium profits under GD/PM for firm 1 and firm 2, respectively:
4.4. The owners' endogenous choice: the ‘green’ delegation game (GD versus PM)
By using the firms' profits equations given by the expressions in equations (6), (14) and (19), one can get the payoff matrix reported in table 1 for the GD game (GD versus PM). The endogenous choice of firms' owners between being ‘green’ delegated (through the design of a managerial contract based on emissions instead of sales) and profit maximisers is played at the pre-play stage or contract stage of the game.
Table 1. The ‘green’ delegation game under abatement (payoff matrix): GD versus PM

To satisfy the technical conditions given by the feasibility constraints and obtain well-identified equilibria in pure strategies for all strategic profiles studied in the subgames presented in the previous sections, the analysis is confined to the following range of the degree of public environmental awareness toward a clean environment (or against the damage caused by industrial production), $0.20138 < g < 2.305$![]() . The former inequality bounds from below the parameter region, requiring that the societal awareness of a clean environment should be high enough to ensure positive levels of pollution abatement for the managerial firm in the asymmetric subgame, in which the owner of one firm designs a delegation contract based on emissions to its own manager (GD), and the rival is profit maximising (PM) under abatement. The latter inequality bounds from above the parameter region, requiring that the societal awareness toward a clean environment should be low enough (i.e., the emissions tax rate should not be fixed at too high a level) to guarantee that emissions are non-negative for the PM firm in the asymmetric subgame. Within this range of values of g, all other relevant feasibility constraints discussed above are satisfied and apply accordingly.
. The former inequality bounds from below the parameter region, requiring that the societal awareness of a clean environment should be high enough to ensure positive levels of pollution abatement for the managerial firm in the asymmetric subgame, in which the owner of one firm designs a delegation contract based on emissions to its own manager (GD), and the rival is profit maximising (PM) under abatement. The latter inequality bounds from above the parameter region, requiring that the societal awareness toward a clean environment should be low enough (i.e., the emissions tax rate should not be fixed at too high a level) to guarantee that emissions are non-negative for the PM firm in the asymmetric subgame. Within this range of values of g, all other relevant feasibility constraints discussed above are satisfied and apply accordingly.
To derive the Nash equilibria of the game, we study the sign of the following set of profit differentials for firm $i = 1,2$![]() , $i \ne j$
, $i \ne j$![]() :
:

An analytical inspection of the expressions in equation (20) reveals that ${\Delta }{\pi _a}\frac{\lt}{\gt}0$![]() if $0.20138 < g\frac{\lt}{\gt}0.37,\;{\Delta }{\pi _b} < 0$
if $0.20138 < g\frac{\lt}{\gt}0.37,\;{\Delta }{\pi _b} < 0$![]() and ${\Delta }{\pi _c} > 0$
and ${\Delta }{\pi _c} > 0$![]() for any $0.20138 < g < 2.305$
for any $0.20138 < g < 2.305$![]() , from which one can obtain Result 1 (see proof in online appendix B).
, from which one can obtain Result 1 (see proof in online appendix B).
Result 1 If the regulator levies an emissions tax to incentivise firms undertaking emissions-reducing actions, the ‘green’ delegation game (GD versus PM) produces the following set of Nash equilibrium outcomes in pure strategies. (i) If $0.20138 < g < 0.37$![]() , then there exist two pure-strategy Nash equilibria given by (PM,PM) and (GD,GD), and the PM payoff dominates GD (coordination game). (ii) If $0.37 < g < 2.305$
, then there exist two pure-strategy Nash equilibria given by (PM,PM) and (GD,GD), and the PM payoff dominates GD (coordination game). (ii) If $0.37 < g < 2.305$![]() , then (GD,GD) is the unique Pareto-inefficient subgame perfect Nash equilibrium (SPNE) of the game (prisoner's dilemma), and GD is the dominant strategy (there is a conflict between self-interest and the mutual benefit to become a GD firm instead of remaining a PM).
, then (GD,GD) is the unique Pareto-inefficient subgame perfect Nash equilibrium (SPNE) of the game (prisoner's dilemma), and GD is the dominant strategy (there is a conflict between self-interest and the mutual benefit to become a GD firm instead of remaining a PM).
First, we note that asymmetric equilibria are prevented as the model does not include elements affecting one firm differently from the rival. The economic intuition of the Nash equilibrium outcomes of the GD game can be carried out following the narrative of the cases detailed in Result 1, starting from low values of the societal awareness towards a clean environmental quality (alternatively, against the – severe or mild – environmental damages caused by industrial production). If $0.20138 < g < 0.37$![]() , there are multiple pure-strategy Nash equilibria in which the PM payoff dominates GD. When g is sufficiently low, the optimal tax rates under PM and GD are low. As ${t^{\mathrm{\ast GD}/{\rm GD}}} > {t^{\mathrm{\ast PM}/{\rm PM}}}$
, there are multiple pure-strategy Nash equilibria in which the PM payoff dominates GD. When g is sufficiently low, the optimal tax rates under PM and GD are low. As ${t^{\mathrm{\ast GD}/{\rm GD}}} > {t^{\mathrm{\ast PM}/{\rm PM}}}$![]() , profits under GD/GD are smaller than profits under PM/PM, though the post-tax equilibrium values of industrial production and abatement are the same in both cases. In addition, in the GD scenario, some resources should also be devoted to executive remuneration, but the amount of the optimal emissions tax at the equilibrium exactly compensates the reduced abatement of the ‘green’ manager due to the incentives designed by the owner through a contract based on emissions.
, profits under GD/GD are smaller than profits under PM/PM, though the post-tax equilibrium values of industrial production and abatement are the same in both cases. In addition, in the GD scenario, some resources should also be devoted to executive remuneration, but the amount of the optimal emissions tax at the equilibrium exactly compensates the reduced abatement of the ‘green’ manager due to the incentives designed by the owner through a contract based on emissions.
The combination of the effects within this range of values of g implies a drop in profits in all (symmetric and asymmetric) strategic profiles following an increase in g, as the negative effects on profits of the reduction in the amount of industrial production overcomes the positive effects due to the increase in the market price. However, the percentage reduction in profits is larger under PM than under GD in both symmetric and asymmetric subgames. This is partly because production under GD in the asymmetric subgame is larger than under PM.
In addition, ceteris paribus, the overall burden of the emissions tax under GD is larger than under PM, and this provides an incentive for firms not to deviate toward GD if the rival also chooses to be a ‘green’-delegated firm. No dominant strategies exist in this case. Definitively, the outcome of the game is a priori uncertain. In fact, on the one hand, each player is interested in PM if the rival chooses not to be ‘green’ delegated, because everyone would like to play PM. On the other hand, no one is willing to play GD if the rival plays PM, as no one wants to be the sole player to get lower profits. Again, no one would like to make decisions that they might regret, but no one can foresee the rival's decisions (this is because firms are playing a simultaneous non-cooperative game).
It could happen, however, that the two players make non-consistent choices: if someone chooses to play GD to avoid losing the opportunity to get higher profits and the rival chooses PM to reduce the tax burden, players could end up in a situation in which only one is ‘green’ delegated, representing for both an unsatisfactory outcome, as everyone could be better off with a different choice.
Differently, if decisions were compatible, both players would choose to be profit maximisers if they are willing to reduce the tax burden in a context in which social awareness against pollution is not sufficiently high, thus achieving a Pareto-efficient outcome. Players could also make compatible decisions ensuring a sub-optimal result, and thus they can both choose to be ‘green’ delegated if they are willing to avoid being the sole PM player experiencing the worst outcome.
In this context, however, players are interested in agreeing to be PM. Furthermore, by choosing PM, everyone becomes interested in complying with the non-binding agreement, as no one would have the incentive to deviate towards GD. Though the game is non-cooperative, both players have an incentive to coordinate towards PM by not designing a managerial delegation contract based on emissions.
If $0.37 < g < 2.305$![]() , the comparison between profits under GD and PM supports the strategic profile GD. Indeed, the percentage reduction in profits under PM is larger than under GD as g increases. This is because, in the asymmetric subgame GD/PM, the GD firm produces more and abates less than the PM firm due to the design of the contract based on emissions so that $\pi _1^{\mathrm{\ast GD}/{\rm PM}} > \pi _2^{\mathrm{\ast GD}/{\rm PM}}$
, the comparison between profits under GD and PM supports the strategic profile GD. Indeed, the percentage reduction in profits under PM is larger than under GD as g increases. This is because, in the asymmetric subgame GD/PM, the GD firm produces more and abates less than the PM firm due to the design of the contract based on emissions so that $\pi _1^{\mathrm{\ast GD}/{\rm PM}} > \pi _2^{\mathrm{\ast GD}/{\rm PM}}$![]() . The optimal emissions tax in the asymmetric subgame GD/PM is set at an intermediate value between the symmetric subgames GD/GD (the highest) and PM/PM (the lowest), so that the government is not able induce the GD firm to sufficiently increase pollution abatement in the asymmetric case. Therefore, though in the asymmetric subgame the GD firm gets a higher tax burden $\left({t^{\ast {\rm GD}/{\rm PM}}}\left(q_1^{\ast {\rm GD}/{\rm PM}} - k_1^{\ast {\rm GD}/{\rm PM}}\right)\right)$
. The optimal emissions tax in the asymmetric subgame GD/PM is set at an intermediate value between the symmetric subgames GD/GD (the highest) and PM/PM (the lowest), so that the government is not able induce the GD firm to sufficiently increase pollution abatement in the asymmetric case. Therefore, though in the asymmetric subgame the GD firm gets a higher tax burden $\left({t^{\ast {\rm GD}/{\rm PM}}}\left(q_1^{\ast {\rm GD}/{\rm PM}} - k_1^{\ast {\rm GD}/{\rm PM}}\right)\right)$![]() than the PM firm $\left({t^{\mathrm{\ast GD}/{\rm PM}}}\left(q_2^{\mathrm{\ast GD}/{\rm PM}} - k_2^{\mathrm{\ast GD}/{\rm PM}}\right)\right)$
than the PM firm $\left({t^{\mathrm{\ast GD}/{\rm PM}}}\left(q_2^{\mathrm{\ast GD}/{\rm PM}} - k_2^{\mathrm{\ast GD}/{\rm PM}}\right)\right)$![]() , profits of the GD firm $\pi _1^{\mathrm{\ast GD}/{\rm PM}}$
, profits of the GD firm $\pi _1^{\mathrm{\ast GD}/{\rm PM}}$![]() decrease when g increases but remain higher than profits of the PM rival $\pi _2^{\mathrm{\ast GD}/{\rm PM}}$
decrease when g increases but remain higher than profits of the PM rival $\pi _2^{\mathrm{\ast GD}/{\rm PM}}$![]() that decrease at a higher rate following an increase in g. As the inequality $\pi _2^{\mathrm{\ast PM}/{\rm PM}} > \pi _2^{\mathrm{\ast PM}/{\rm GD}}$
that decrease at a higher rate following an increase in g. As the inequality $\pi _2^{\mathrm{\ast PM}/{\rm PM}} > \pi _2^{\mathrm{\ast PM}/{\rm GD}}$![]() holds for any $g < 0.37$
holds for any $g < 0.37$![]() , one gets $\pi _2^{\mathrm{\ast PM}/{\rm PM}} < \pi _2^{\mathrm{\ast PM}/{\rm GD}}$
, one gets $\pi _2^{\mathrm{\ast PM}/{\rm PM}} < \pi _2^{\mathrm{\ast PM}/{\rm GD}}$![]() for any $g > 0.37$
for any $g > 0.37$![]() . Consequently, the increased awareness toward environmental quality allows GD to become the dominant strategy of the game. This outcome, however, is Pareto inefficient for firms, as they both would jointly deviate toward PM to benefit from a reduction in the tax burden, reduce the marginal costs and obtain higher profits. Therefore, there is a conflict between self-interest and mutual benefit not to become a ‘green’-delegated firm.
. Consequently, the increased awareness toward environmental quality allows GD to become the dominant strategy of the game. This outcome, however, is Pareto inefficient for firms, as they both would jointly deviate toward PM to benefit from a reduction in the tax burden, reduce the marginal costs and obtain higher profits. Therefore, there is a conflict between self-interest and mutual benefit not to become a ‘green’-delegated firm.
5. Sales delegation (SD) versus profit maximisation (PM) with homogeneous products
This section aims at studying the endogenous choice played at the pre-play stage (or contract stage) of the game between choosing SD or PM augmented with abatement decisions and emissions taxes. The subgame referred to as PM under abatement is the same as the one presented in section 4.1. Therefore, we can concentrate on the universal adoption of SD and the asymmetric case in which only one firm becomes sales delegated.
5.1 The symmetric subgame SD/SD
Consider the case in which owners offer a standard output (sales) delegation contract to a manager who must choose both output and abatement levels. The utility function of the manager changes from equation (7) to take the standard form pioneered in the managerial delegation literature by Vickers (Reference Vickers1985), Sklivas (Reference Sklivas1987) and Fershtman and Judd (Reference Fershtman and Judd1987). That is:
Equation (21) is a linear combination weighting profits and sales, where ${\pi _i}$![]() and ${b_i}$
and ${b_i}$![]() are defined as in the previous section. The maximisation of the managers' utility function in equation (21) at the market stage of the game with respect to ${q_i}$
are defined as in the previous section. The maximisation of the managers' utility function in equation (21) at the market stage of the game with respect to ${q_i}$![]() and ${k_i}$
and ${k_i}$![]() yields the following first-order conditions:
yields the following first-order conditions:
where the superscript SD/SD stands for sales delegation of both managers. Solving the system of output reaction functions $\bar{q}_i^{{\rm SD/SD}}$![]() in equation (22), one gets the same solution as in equation (9), i.e., $q_i^{{\rm SD/SD}} = q_i^{{\rm GD/GD}}$
in equation (22), one gets the same solution as in equation (9), i.e., $q_i^{{\rm SD/SD}} = q_i^{{\rm GD/GD}}$![]() . Substituting equation (9) and $k_i^{{\rm SD/SD}} = t$
. Substituting equation (9) and $k_i^{{\rm SD/SD}} = t$![]() into equation (1) allows us to obtain firm $i$
into equation (1) allows us to obtain firm $i$![]() 's profits as a function of the managerial bonuses ${b_i}$
's profits as a function of the managerial bonuses ${b_i}$![]() and ${b_j}$
and ${b_j}$![]() and the tax rate t. Comparison of the expressions in equations (2), (8) and (22) reveals that, at the pre-tax market stage of the game, the sales manager under an abatement regime is incentivised to produce the same amount and abate more than the ‘green’ manager (indeed the abated pollutant under the SD regime is the same as in the PM regime at this stage) as the former is incentivised by a contract based on sales and the latter by a contract based on emissions.
and the tax rate t. Comparison of the expressions in equations (2), (8) and (22) reveals that, at the pre-tax market stage of the game, the sales manager under an abatement regime is incentivised to produce the same amount and abate more than the ‘green’ manager (indeed the abated pollutant under the SD regime is the same as in the PM regime at this stage) as the former is incentivised by a contract based on sales and the latter by a contract based on emissions.
This section will also show that the design of the SD contract by the owner is such that the welfare-maximising emissions tax levied by the government at the government stage in the SD regime is set at an intermediate level between the optimal tax rate in the GD regime (the highest) and the optimal tax rate in the PM regime (the smallest). This is because production under SD is higher than under PM and abatement under SD is higher than under GD. In addition, the owner under SD will set a bonus larger than under GD as the pre-tax quantities are the same but abatement (which is not part of the contract under SD) is larger in the SD regime. This eventually implies that equilibrium production and abatement at the post-tax stage of the game under SD are the highest. The largest production under SD causes however the largest levels of aggregate emissions and environmental damage compared to the other two contracts by also implying that the SD firm will incur higher marginal costs and lower equilibrium post-tax profits than the GD firms.
Comparison amongst the crucial values obtained under SD and GD contracts (as will be clear later) implies that at the post-tax stage the working of the policy-driven mechanism – based on a transfer of resources flowing from firms to the public authority – does not allow the government to perfectly compensate the increased emissions of the SD regime as the optimal emissions tax rate is smaller than in the GD regime.
At the bonus stage, firm $i$![]() 's owner $(i = 1,2)$
's owner $(i = 1,2)$![]() maximises profits with respect to ${b_i}$
maximises profits with respect to ${b_i}$![]() , obtaining the reaction functions in the bonus space $\bar{b}_i^{{\rm SD/SD}} = (1/4)(1 - t - {b_j}),\;i = 1,2,\;i \ne j$
, obtaining the reaction functions in the bonus space $\bar{b}_i^{{\rm SD/SD}} = (1/4)(1 - t - {b_j}),\;i = 1,2,\;i \ne j$![]() . Therefore, the symmetric equilibrium value of the bonus as a function of the tax rate is:
. Therefore, the symmetric equilibrium value of the bonus as a function of the tax rate is:
We first note that $b_i^{{\rm SD/SD}} > b_i^{{\rm GD/GD}}$![]() . This is because the sales manager is incentivised to produce the same amount and abate more than the ‘green’ manager (who is incentivised by a contract based on emissions rather than sales) at the (pre-tax) market stage of the game. Further substitutions using the expression in equation (23) and other relevant equations yield the equilibrium expressions for the producer surplus $({\rm P}{{\rm S}^{{\rm SD/SD}}})$
. This is because the sales manager is incentivised to produce the same amount and abate more than the ‘green’ manager (who is incentivised by a contract based on emissions rather than sales) at the (pre-tax) market stage of the game. Further substitutions using the expression in equation (23) and other relevant equations yield the equilibrium expressions for the producer surplus $({\rm P}{{\rm S}^{{\rm SD/SD}}})$![]() , consumer surplus $({\rm C}{{\rm S}^{{\rm SD/SD}}})$
, consumer surplus $({\rm C}{{\rm S}^{{\rm SD/SD}}})$![]() , tax revenues $({\rm T}{{\rm R}^{{\rm SD/SD}}})$
, tax revenues $({\rm T}{{\rm R}^{{\rm SD/SD}}})$![]() and environmental damage $({\rm E}{{\rm D}^{{\rm SD/SD}}})$
and environmental damage $({\rm E}{{\rm D}^{{\rm SD/SD}}})$![]() as a function of the tax rate when both firms are sales delegated under abatement (reported in online appendix B), allowing one to get social welfare under SD/SD $({\rm S}{{\rm W}^{{\rm SD/SD}}} = {\rm P}{{\rm S}^{{\rm SD/SD}}} + {\rm C}{{\rm S}^{{\rm SD/SD}}} + {\rm T}{{\rm R}^{{\rm SD/SD}}} - {\rm E}{{\rm D}^{{\rm SD/SD}}})$
as a function of the tax rate when both firms are sales delegated under abatement (reported in online appendix B), allowing one to get social welfare under SD/SD $({\rm S}{{\rm W}^{{\rm SD/SD}}} = {\rm P}{{\rm S}^{{\rm SD/SD}}} + {\rm C}{{\rm S}^{{\rm SD/SD}}} + {\rm T}{{\rm R}^{{\rm SD/SD}}} - {\rm E}{{\rm D}^{{\rm SD/SD}}})$![]() , which is reported in lemma 4.
, which is reported in lemma 4.
Lemma 4 The social welfare function under SD/SD as a function of the tax rate is given by:
At the first stage of the subgame, the government levies an emissions tax with the aim of maximising social welfare. Proposition 4 shows the extent of the welfare-maximising tax rate ${{t}^{{\ast} {\rm SD}/{\rm SD}}}$![]() and the condition under which the optimal tax rate in the subgame SD/SD is positive (see proofs of lemma 4 and proposition 4 in online appendix B).
and the condition under which the optimal tax rate in the subgame SD/SD is positive (see proofs of lemma 4 and proposition 4 in online appendix B).
Proposition 4 The welfare-maximising tax rate under SD/SD is given by the following expression, which is positive if and only if $g > 0.07142$![]() :
:
Using the optimal tax rate in equation (25), one obtains the equilibrium quantities of industrial production $q_i^{\mathrm{\ast SD/SD}} = ((14(2g + 1))/(98g + 33)) > 0$![]() , executive remuneration $b_i^{\mathrm{\ast SD/SD}} = ((7(2g + 1))/(98g + 33)) > 0$
, executive remuneration $b_i^{\mathrm{\ast SD/SD}} = ((7(2g + 1))/(98g + 33)) > 0$![]() , abatement $k_i^{\mathrm{\ast SD/SD}} = ((2(14g - 1))/(98g + 33)) > 0$
, abatement $k_i^{\mathrm{\ast SD/SD}} = ((2(14g - 1))/(98g + 33)) > 0$![]() for any $g > 0.07142$
for any $g > 0.07142$![]() , and emissions $q_i^{\mathrm{\ast SD/SD}} - k_i^{\mathrm{\ast SD/SD}} > 0$
, and emissions $q_i^{\mathrm{\ast SD/SD}} - k_i^{\mathrm{\ast SD/SD}} > 0$![]() . Finally, inserting back the optimal tax ${t^{\mathrm{\ast SD/SD}}}$
. Finally, inserting back the optimal tax ${t^{\mathrm{\ast SD/SD}}}$![]() into the profit function in equation (1), one gets equilibrium profits under SD/SD, that is:
into the profit function in equation (1), one gets equilibrium profits under SD/SD, that is:
Before analysing the asymmetric subgame SD/PM and the endogenous choice at the pre-play stage between choosing to become sales delegated under pollution abatement or remaining a profit-maximising firm, it is useful to compare emissions taxes, profits, quantities, abatements, executive remunerations (bonuses), emissions and environmental damages in the symmetric subgames GD/GD, SD/SD, and PM/PM, as asymmetric Nash equilibrium outcomes are prevented in the different models of the article.
Given the results obtained in the previous sections, it is easy to see that the following sets of inequalities hold (for any $g$![]() ) at the post-tax equilibrium stage: ${t^{\ast {\rm GD/GD}}} > {t^{\mathrm{\ast SD/SD}}} > {t^{\ast {\rm PM/PM}}},\;\pi _i^{\mathrm{\ast PM/PM}} > \pi _i^{\mathrm{\ast GD/GD}} > \pi _i^{\mathrm{\ast SD/SD}}, q_i^{\mathrm{\ast SD/SD}} \,{\gt}\, q_i^{\mathrm{\ast GD/GD}} \,{=}\, q_i^{\mathrm{\ast PM/PM}}, k_i^{\mathrm{\ast SD/SD}} > k_i^{\mathrm{\ast GD/GD}} = k_i^{\mathrm{\ast PM/PM}},\ b_i^{\mathrm{\ast SD/SD}} > b_i^{\mathrm{\ast GD/GD}},\ e_i^{\mathrm{\ast SD/SD}} > e_i^{\mathrm{\ast GD/GD}} = e_i^{\mathrm{\ast PM/PM}}$
) at the post-tax equilibrium stage: ${t^{\ast {\rm GD/GD}}} > {t^{\mathrm{\ast SD/SD}}} > {t^{\ast {\rm PM/PM}}},\;\pi _i^{\mathrm{\ast PM/PM}} > \pi _i^{\mathrm{\ast GD/GD}} > \pi _i^{\mathrm{\ast SD/SD}}, q_i^{\mathrm{\ast SD/SD}} \,{\gt}\, q_i^{\mathrm{\ast GD/GD}} \,{=}\, q_i^{\mathrm{\ast PM/PM}}, k_i^{\mathrm{\ast SD/SD}} > k_i^{\mathrm{\ast GD/GD}} = k_i^{\mathrm{\ast PM/PM}},\ b_i^{\mathrm{\ast SD/SD}} > b_i^{\mathrm{\ast GD/GD}},\ e_i^{\mathrm{\ast SD/SD}} > e_i^{\mathrm{\ast GD/GD}} = e_i^{\mathrm{\ast PM/PM}}$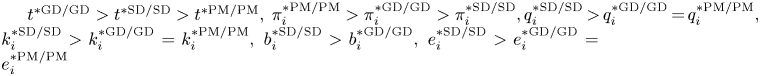 and $E{D^{\ast SD/SD}} > E{D^{\ast GD/GD}} = E{D^{\ast PM/PM}}$
and $E{D^{\ast SD/SD}} > E{D^{\ast GD/GD}} = E{D^{\ast PM/PM}}$![]() . This allows us to conclude that the GD contract works in the eco-friendly direction of reducing emissions and environmental damages compared to the standard SD contract under pollution abatement, while also giving firms the opportunity to generate higher profits than the strategic profile SD/SD (this is because marginal costs are higher in the SD scenario than in the GD scenario).
. This allows us to conclude that the GD contract works in the eco-friendly direction of reducing emissions and environmental damages compared to the standard SD contract under pollution abatement, while also giving firms the opportunity to generate higher profits than the strategic profile SD/SD (this is because marginal costs are higher in the SD scenario than in the GD scenario).
In addition, according to the study of the optimal bonus functions, it follows that the higher the public awareness towards environmental quality, the smaller the incentive to pollute. The relationship between ${b_i}$![]() and g is ‘green’ oriented, as polluting production reduces the incentive for the manager to pollute. We want to stress that we initially referred to the ‘green’-related strategic profile as ‘GD’ but do not know in advance whether the introduction of emissions instead of sales in the manager's utility is eco-friendly or anti-ecological. However, equilibrium results lie indeed within an eco-friendly trajectory.
and g is ‘green’ oriented, as polluting production reduces the incentive for the manager to pollute. We want to stress that we initially referred to the ‘green’-related strategic profile as ‘GD’ but do not know in advance whether the introduction of emissions instead of sales in the manager's utility is eco-friendly or anti-ecological. However, equilibrium results lie indeed within an eco-friendly trajectory.
5.2 The asymmetric subgame SD/PM
To derive the owners' endogenous choice of whether to become a sales-delegated firm or remain a profit maximiser under abatement, one must compute the outcomes of the asymmetric game in which one firm, say firm 1, is sales delegated, ${b_1} \ne 0$![]() , and the rival, firm 2, is profit maximising, ${b_2} = 0$
, and the rival, firm 2, is profit maximising, ${b_2} = 0$![]() (SD/PM). The two optimisation problems at the market stage of the game lead to first-order conditions as in equation (22) for SD firm 1 and as in equation (2) for PM firm 2. Solving the system of the output reaction functions, one obtains the output levels as in equation (15). Substituting these outcomes along with condition $k_1^{{\rm SD/PM}} = t$
(SD/PM). The two optimisation problems at the market stage of the game lead to first-order conditions as in equation (22) for SD firm 1 and as in equation (2) for PM firm 2. Solving the system of the output reaction functions, one obtains the output levels as in equation (15). Substituting these outcomes along with condition $k_1^{{\rm SD/PM}} = t$![]() into the profit function of the SD firm, one gets the expression of firm 1's profits as a function of the managerial incentive. It follows that firm 1's owner maximises profits with respect to ${b_1}$
into the profit function of the SD firm, one gets the expression of firm 1's profits as a function of the managerial incentive. It follows that firm 1's owner maximises profits with respect to ${b_1}$![]() at the bonus stage, leading to the optimal bonus as a function of the tax rate, that is $b_1^{{\rm SD/PM}} = (1/4)({1 - t} )$
at the bonus stage, leading to the optimal bonus as a function of the tax rate, that is $b_1^{{\rm SD/PM}} = (1/4)({1 - t} )$![]() . Therefore, the subgame equilibrium outcomes as a function of the tax rate are:
. Therefore, the subgame equilibrium outcomes as a function of the tax rate are:
Further substitutions by making use of equation (27) allow us to get the equilibrium expressions for the producer surplus $({\rm P}{{\rm S}^{{\rm SD/PM}}})$![]() , consumer surplus $({\rm C}{{\rm S}^{{\rm SD/PM}}})$
, consumer surplus $({\rm C}{{\rm S}^{{\rm SD/PM}}})$![]() , tax revenues $({\rm T}{{\rm R}^{{\rm SD/PM}}})$
, tax revenues $({\rm T}{{\rm R}^{{\rm SD/PM}}})$![]() and environmental damage ${\rm (E}{{\rm D}^{{\rm SD/PM}}}{\rm )}$
and environmental damage ${\rm (E}{{\rm D}^{{\rm SD/PM}}}{\rm )}$![]() as a function of the tax rate when firm 1 is sales delegated and firm 2 is profit maximising (reported in online appendix B), thus providing social welfare under SD/PM $({\rm S}{{\rm W}^{{\rm SD/PM}}} = {\rm P}{{\rm S}^{{\rm SD/PM}}} + {\rm C}{{\rm S}^{{\rm SD/PM}}} + {\rm T}{{\rm R}^{{\rm SD/PM}}} - {\rm E}{{\rm D}^{{\rm SD/PM}}})$
as a function of the tax rate when firm 1 is sales delegated and firm 2 is profit maximising (reported in online appendix B), thus providing social welfare under SD/PM $({\rm S}{{\rm W}^{{\rm SD/PM}}} = {\rm P}{{\rm S}^{{\rm SD/PM}}} + {\rm C}{{\rm S}^{{\rm SD/PM}}} + {\rm T}{{\rm R}^{{\rm SD/PM}}} - {\rm E}{{\rm D}^{{\rm SD/PM}}})$![]() , which is reported in lemma 5.
, which is reported in lemma 5.
Lemma 5 The social welfare function under SD/PM as a function of the tax rate is given by:
At the first stage of the subgame, the government levies an emissions tax with the aim of maximising social welfare. Proposition 5 shows the extent of the welfare-maximising tax rate ${{t}^{{\ast} {\rm SD}/{\rm PM}}}$![]() and the condition under which the optimal tax rate in the subgame SD/PM is positive (see proofs of lemma 5 and proposition 5 in online appendix B).
and the condition under which the optimal tax rate in the subgame SD/PM is positive (see proofs of lemma 5 and proposition 5 in online appendix B).
Proposition 5 The welfare-maximising tax rate under SD/PM is given by the following expression, which is positive if and only if $g > 0.0909$![]() :
:
Using the optimal tax rate in equation (29), one obtains the equilibrium quantities of industrial production $q_1^{\mathrm{\ast SD/PM}} = (22(2g + 1)/(121g + 41)) > 0,\;q_2^{\mathrm{\ast SD/PM}} = (11 (2g + 1)/(121g + 41)) > 0$![]() , executive remuneration $b_1^{\mathrm{\ast SD/PM}} = (11(2g + 1)/(121g + 41)) > 0$
, executive remuneration $b_1^{\mathrm{\ast SD/PM}} = (11(2g + 1)/(121g + 41)) > 0$![]() , abatement $k_1^{\mathrm{\ast SD/PM}} = k_2^{\mathrm{\ast SD/PM}} = (3(11g - 1)/(121g + 41)) > 0$
, abatement $k_1^{\mathrm{\ast SD/PM}} = k_2^{\mathrm{\ast SD/PM}} = (3(11g - 1)/(121g + 41)) > 0$![]() for any $g > 0.0909$
for any $g > 0.0909$![]() , and emissions $q_1^{\mathrm{\ast SD/PM}} - k_1^{\mathrm{\ast SD/PM}} > 0$
, and emissions $q_1^{\mathrm{\ast SD/PM}} - k_1^{\mathrm{\ast SD/PM}} > 0$![]() and $q_2^{\mathrm{\ast SD/PM}} - k_2^{\mathrm{\ast SD/PM}} > 0$
and $q_2^{\mathrm{\ast SD/PM}} - k_2^{\mathrm{\ast SD/PM}} > 0$![]() for any $0.0909 < g < 1.2727$
for any $0.0909 < g < 1.2727$![]() . Finally, inserting the optimal tax ${t^{\mathrm{\ast SD/PM}}}$
. Finally, inserting the optimal tax ${t^{\mathrm{\ast SD/PM}}}$![]() back into the profit function in equation (1), one gets equilibrium profits under SD/PM for firm 1 and firm 2, respectively:
back into the profit function in equation (1), one gets equilibrium profits under SD/PM for firm 1 and firm 2, respectively:
5.3. The owners' endogenous choice: the sales delegation game (SD versus PM)
By using the firms' profits equations given by the expressions in equations (6), (26) and (30), one can obtain the payoff matrix reported in table 2 about the sales delegation game (SD versus PM) under abatement. The endogenous choice of firms' owners which should choose to be sales delegated (through the design of a managerial contract based on sales) or profit maximisers is played at the pre-play or contract stage of the game.
Table 2. The sales delegation game under abatement (payoff matrix): SD versus PM

To satisfy the technical restrictions given by the feasibility constraints and obtain well-identified equilibria in pure strategies for all strategic profiles studied in the subgames presented in the previous sections, the analysis is confined to the following range of the degree of public environmental awareness toward a clean environment (or against the damage caused by industrial production), $0.125 < g < 1.2727$![]() . The former inequality bounds from below the parameter region requiring that the societal awareness toward a clean environment should be high enough to ensure positive levels of pollution abatement (and the optimal emissions tax rate) for both PM firms in the symmetric subgame PM/PM. The latter inequality bounds from above the parameter region requiring that the societal awareness toward a clean environment should be low enough (i.e., the emissions tax rate should not be fixed at too high a level) to guarantee that emissions are non-negative for the PM firm in the asymmetric subgame in which the owner of one firm designs a SD contract to its own manager and the rival is profit maximising (PM) under abatement. Within this range of values of g, all other relevant feasibility constraints discussed above are satisfied and apply accordingly.
. The former inequality bounds from below the parameter region requiring that the societal awareness toward a clean environment should be high enough to ensure positive levels of pollution abatement (and the optimal emissions tax rate) for both PM firms in the symmetric subgame PM/PM. The latter inequality bounds from above the parameter region requiring that the societal awareness toward a clean environment should be low enough (i.e., the emissions tax rate should not be fixed at too high a level) to guarantee that emissions are non-negative for the PM firm in the asymmetric subgame in which the owner of one firm designs a SD contract to its own manager and the rival is profit maximising (PM) under abatement. Within this range of values of g, all other relevant feasibility constraints discussed above are satisfied and apply accordingly.
To derive the Nash equilibria of the game, we study the sign of the following set of profit differentials for firm $i = 1,2,\;i \ne j$![]() :
:

An analytical inspection of the expressions in equation (31) reveals that ${\Delta }{\pi _a} > 0, {\Delta }{\pi _b} < 0$![]() and ${\Delta }{\pi _c} > 0$
and ${\Delta }{\pi _c} > 0$![]() for any $0.125 < g < 1.2727$
for any $0.125 < g < 1.2727$![]() , from which one can obtain the following result (see proof in online appendix B).
, from which one can obtain the following result (see proof in online appendix B).
Result 2 If the regulator levies an emissions tax to incentivise firms undertaking emissions-reduction actions, the sales delegation game SD versus PM with pollution abatement produces the following Nash equilibrium outcome in pure strategies: (SD, SD) is the unique Pareto inefficient SPNE of the game (prisoner's dilemma), and SD is the dominant strategy (there is a conflict between self-interest and the mutual benefit to become a sales-delegated firm).
Result 2 resembles the standard result of Vickers (Reference Vickers1985), Fershtman and Judd (Reference Fershtman and Judd1987) and Sklivas (Reference Sklivas1987) – hereafter VFJS – in which SD is the dominant strategy but firms are entrapped in a prisoner's dilemma. This suggests that augmenting the SD game with pollution abatement does not change the main message of the SD literature framed in strategic competitive markets if products are homogeneous. In this regard, we pinpoint that considering the endogenous choice of the standard SD game without abatement (i.e., SD versus PM following the VFJS approach) leads to the well-known conclusion that the SD contract emerges as the unique pure-strategy Pareto inefficient Nash equilibrium of the game in either case of homogeneous and heterogeneous products if the manager's bonus is unilaterally chosen by the owner, though results may dramatically change if owners and managers are engaged in bargaining to choose executive remuneration (see Fanti et al., Reference Fanti, Gori and Sodini2017b), as the bargaining power interacts with the extent of product differentiation in determining the Nash equilibrium outcomes of the game. This can be very different from the classic VFJS result, according to which the SD contract without abatement is always the dominant strategy and the SD game falls under the paradigm of the prisoner's dilemma. Unlike this outcome, building on the sales delegation game (SD versus PM) under abatement can greatly modify the Nash equilibrium results of the traditional VFJS literature also in the absence of a bargaining mechanism between owners and managers over managerial contracts just by assuming horizontal product differentiation, allowing for the existence of a plethora of different Nash equilibrium outcomes depending on the interaction between the degree of product differentiation and the public awareness towards environmental quality (see online appendix C, figure A5 for details).
6. ‘Green’ delegation (GD) versus sales delegation (SD) with homogeneous products
This section investigates a delegation game in which the owners offer their own managers either a GD contract based on emissions or a standard SD contract under pollution abatement. The section deals explicitly with the asymmetric subgame GD/SD as the symmetric subgames GD/GD and SD/SD were the subjects of sections 4.2 and 5.1, respectively.
6.1 The asymmetric subgame GD/SD
The owners' endogenous choice about the type of delegation contract to be designed in this case needs the evaluation of the payoffs of the asymmetric game in which the owner of one firm, say firm 1, designs a delegation contract based on emissions and the rival, firm 2, designs an SD contract. The two managers' maximisation problems give the first-order conditions presented in section 4.2 for the GD firm 1 and in section 5.1 for the SD firm 2.
Solving the system of the output reaction functions at the market stage of the game, one gets the quantities of industrial production as a function of the managerial incentives as in equation (9). By substituting these outcomes along with (i) the condition $k_1^{{\rm GD/SD}} = t - {b_1}$![]() into the profit function of firm 1, and (ii) the condition $k_2^{{\rm GD/SD}} = t$
into the profit function of firm 1, and (ii) the condition $k_2^{{\rm GD/SD}} = t$![]() into the profit function of firm 2, one obtains the expressions of the firms' profits as a function of the managerial incentives. It follows that, at the bonus stage, the owner of firm 1 maximises ${\pi _1}$
into the profit function of firm 2, one obtains the expressions of the firms' profits as a function of the managerial incentives. It follows that, at the bonus stage, the owner of firm 1 maximises ${\pi _1}$![]() with respect to ${b_1}$
with respect to ${b_1}$![]() , and the owner of firm 2 maximises ${\pi _2}$
, and the owner of firm 2 maximises ${\pi _2}$![]() with respect to ${b_2}$
with respect to ${b_2}$![]() . This generates the system of bonus reaction functions $\bar{b}_1^{{\rm GD/SD}} = (1/13)(1 - t - {b_2})$
. This generates the system of bonus reaction functions $\bar{b}_1^{{\rm GD/SD}} = (1/13)(1 - t - {b_2})$![]() and $\bar{b}_2^{{\rm GD/SD}} = (1/4)(1 - t - {b_1})$
and $\bar{b}_2^{{\rm GD/SD}} = (1/4)(1 - t - {b_1})$![]() , whose solutions lead to the optimal bonuses as a function of the tax rate, that is, $b_1^{{\rm GD/SD}} = (1/17)(1 - t)$
, whose solutions lead to the optimal bonuses as a function of the tax rate, that is, $b_1^{{\rm GD/SD}} = (1/17)(1 - t)$![]() and $b_2^{{\rm GD/SD}} = (1/17)(4 - t)$
and $b_2^{{\rm GD/SD}} = (1/17)(4 - t)$![]() , so that $b_2^{{\rm GD/SD}} > b_1^{{\rm GD/SD}}$
, so that $b_2^{{\rm GD/SD}} > b_1^{{\rm GD/SD}}$![]() (in line with the results of sections 4 and 5). Therefore, the equilibrium values of quantities and abatement as a function of the tax rate in this asymmetric subgame are:
(in line with the results of sections 4 and 5). Therefore, the equilibrium values of quantities and abatement as a function of the tax rate in this asymmetric subgame are:

From the expressions in equation (32), the inequalities $q_2^{{\rm GD/SD}} > q_1^{{\rm GD/SD}}$![]() and $k_2^{{\rm GD/SD}} > k_1^{{\rm GD/SD}}$
and $k_2^{{\rm GD/SD}} > k_1^{{\rm GD/SD}}$![]() (in line with the results of sections 4 and 5). Further substitutions through the use of equation (32) allow us to get the equilibrium expressions for the producer surplus $({\rm P}{{\rm S}^{{\rm GD/SD}}})$
(in line with the results of sections 4 and 5). Further substitutions through the use of equation (32) allow us to get the equilibrium expressions for the producer surplus $({\rm P}{{\rm S}^{{\rm GD/SD}}})$![]() , consumer surplus $({\rm C}{{\rm S}^{{\rm GD/SD}}})$
, consumer surplus $({\rm C}{{\rm S}^{{\rm GD/SD}}})$![]() , tax revenues $({\rm T}{{\rm R}^{{\rm GD/SD}}})$
, tax revenues $({\rm T}{{\rm R}^{{\rm GD/SD}}})$![]() and environmental damage $({\rm E}{{\rm D}^{{\rm GD/SD}}})$
and environmental damage $({\rm E}{{\rm D}^{{\rm GD/SD}}})$![]() as a function of the tax rate when firm 1 is ‘green’ delegated and firm 2 is sales delegated (reported in online appendix B), providing social welfare under GD/SD $({\rm S}{{\rm W}^{{\rm GD/SD}}} = {\rm P}{{\rm S}^{{\rm GD/SD}}} + {\rm C}{{\rm S}^{{\rm GD/SD}}} + {\rm T}{{\rm R}^{{\rm GD/SD}}} - {\rm E}{{\rm D}^{{\rm GD/SD}}})$
as a function of the tax rate when firm 1 is ‘green’ delegated and firm 2 is sales delegated (reported in online appendix B), providing social welfare under GD/SD $({\rm S}{{\rm W}^{{\rm GD/SD}}} = {\rm P}{{\rm S}^{{\rm GD/SD}}} + {\rm C}{{\rm S}^{{\rm GD/SD}}} + {\rm T}{{\rm R}^{{\rm GD/SD}}} - {\rm E}{{\rm D}^{{\rm GD/SD}}})$![]() , which is reported in lemma 6.
, which is reported in lemma 6.
Lemma 6 The social welfare function under GD/SD as a function of the tax rate is given by:
At the first stage of the subgame, the government levies an emissions tax with the aim of maximising social welfare. Proposition 6 shows the extent of the welfare-maximising tax rate ${{t}^{{\ast} {\rm GD}/{\rm SD}}}$![]() and the condition under which the optimal tax rate in the subgame GD/SD is positive (see proofs of lemma 6 and proposition 6 in online appendix B).
and the condition under which the optimal tax rate in the subgame GD/SD is positive (see proofs of lemma 6 and proposition 6 in online appendix B).
Proposition 6 The welfare-maximising tax rate under GD/SD is given by the following expression, which is positive if and only if $g > 0.0506$![]() :
:
where ${t^{\mathrm{\ast SD/SD}}} < {t^{\mathrm{\ast GD/SD}}} < {t^{\mathrm{\ast GD/GD}}}.$![]()
Using the optimal tax rate in equation (34), one obtains the equilibrium quantities of industrial production $q_1^{\mathrm{\ast GD/SD}} = (120(2g + 1)/ (1152g + 391)) > 0,\;q_2^{\mathrm{\ast GD/SD}} = (192(2g + 1)/ (1152g + 391)) > 0$![]() , executive remunerations $b_1^{\mathrm{\ast GD/SD}} = (24(2g + 1)/ (1152g + 391)) > 0$
, executive remunerations $b_1^{\mathrm{\ast GD/SD}} = (24(2g + 1)/ (1152g + 391)) > 0$![]() and $b_2^{\mathrm{\ast GD/SD}} = (96(2g + 1)/(1152g + 391)) > 0$
and $b_2^{\mathrm{\ast GD/SD}} = (96(2g + 1)/(1152g + 391)) > 0$![]() , abatement $k_1^{\mathrm{\ast GD/SD}} = ((288g - 41)/(1152g + 391)) > 0$
, abatement $k_1^{\mathrm{\ast GD/SD}} = ((288g - 41)/(1152g + 391)) > 0$![]() for any $g > 0.1423,\;k_2^{\mathrm{\ast GD/SD}} = ((336g - 17)/(1152g + 391)) > 0$
for any $g > 0.1423,\;k_2^{\mathrm{\ast GD/SD}} = ((336g - 17)/(1152g + 391)) > 0$![]() for any $g > 0.0506$
for any $g > 0.0506$![]() , and emissions $q_1^{\mathrm{\ast GD/SD}} - k_1^{\mathrm{\ast GD/SD}} > 0$
, and emissions $q_1^{\mathrm{\ast GD/SD}} - k_1^{\mathrm{\ast GD/SD}} > 0$![]() for any $0.1423 < g < 3.3541,\;q_2^{\mathrm{\ast GD/SD}} - k_2^{\mathrm{\ast GD/SD}} > 0,$
for any $0.1423 < g < 3.3541,\;q_2^{\mathrm{\ast GD/SD}} - k_2^{\mathrm{\ast GD/SD}} > 0,$![]() . Finally, inserting the optimal tax ${t^{\mathrm{\ast GD/SD}}}$
. Finally, inserting the optimal tax ${t^{\mathrm{\ast GD/SD}}}$![]() back into the profit function in equation (1), one gets equilibrium profits under GD/SD for firm 1 and firm 2, respectively:
back into the profit function in equation (1), one gets equilibrium profits under GD/SD for firm 1 and firm 2, respectively:
where $\pi _2^{\mathrm{\ast GD/SD}} > \pi _1^{\mathrm{\ast GD/SD}}$![]() .
.
6.2 The owners' endogenous choice: ‘green’ versus sales delegation (GD versus SD)
By using the firms' profits equations given by the expressions in equations (14), (26) and (35), one can obtain the payoff matrix reported in table 3 about the game ‘green’ versus sales delegation (GD versus SD). The endogenous choice of firms' owners, which should choose to be ‘green’ delegated or sales delegated (through the design of a managerial contract based on emissions or sales) is played at the pre-play or contract stage of the game.
Table 3. ‘Green’ delegation versus sales delegation (payoff matrix): GD versus SD

To satisfy the technical restrictions given by the feasibility constraints and obtain well-identified equilibria in pure strategies for all strategic profiles studied in the subgames presented in the previous sections, the analysis is bounded by the following range of the degree of public environmental awareness toward a clean environment (or against the damage caused by industrial production), $0.1423 < g < 3.3541$![]() . The former inequality bounds from below the parameter region requiring that the societal awareness toward a clean environment be high enough to ensure positive levels of pollution abatement (and the optimal emissions tax rate) for the GD firm in the asymmetric subgame GD/SD. That is, when the owner of one firm designs a GD contract based on emissions to his own manager (GD) and the owner of the rival firm designs a delegation contract based on sales to his own manager (SD) under pollution abatement. The latter inequality bounds from above the parameter region requiring that the societal awareness toward a clean environment be low enough (i.e., the emissions tax rate should not be fixed at too high a level) to guarantee that emissions are non-negative for the GD firm in the asymmetric subgame. Within this range of values of g, all other relevant feasibility constraints discussed above are satisfied and apply accordingly.
. The former inequality bounds from below the parameter region requiring that the societal awareness toward a clean environment be high enough to ensure positive levels of pollution abatement (and the optimal emissions tax rate) for the GD firm in the asymmetric subgame GD/SD. That is, when the owner of one firm designs a GD contract based on emissions to his own manager (GD) and the owner of the rival firm designs a delegation contract based on sales to his own manager (SD) under pollution abatement. The latter inequality bounds from above the parameter region requiring that the societal awareness toward a clean environment be low enough (i.e., the emissions tax rate should not be fixed at too high a level) to guarantee that emissions are non-negative for the GD firm in the asymmetric subgame. Within this range of values of g, all other relevant feasibility constraints discussed above are satisfied and apply accordingly.
To derive the Nash equilibria of the game, we study the sign of the following set of profit differentials for firm $i = 1,2,\;i \ne j$![]() :
:

An analytical inspection of the expressions in equation (36) reveals that ${\Delta }{\pi _a} < 0, {\Delta }{\pi _b} > 0$![]() , and ${\Delta }{\pi _c} < 0$
, and ${\Delta }{\pi _c} < 0$![]() for any $0.1423 < g < 3.3541$
for any $0.1423 < g < 3.3541$![]() , from which one can obtain Result 3 (see proof in online appendix B).
, from which one can obtain Result 3 (see proof in online appendix B).
Result 3 If the regulator levies an emissions tax to incentivise firms undertaking emissions-reducing actions, the ‘green’ versus sales delegation game GD versus SD with pollution abatement produces the following Nash equilibrium outcome in pure strategies: (SD,SD) is the unique Pareto-inefficient SPNE of the game (prisoner's dilemma), and SD is the dominant strategy (there is a conflict between self-interest and the mutual benefit to become a sales-delegated firm). This gives each owner the unilateral incentive to design a GD contract based on emissions rather than a delegation contract based on sales when firms adopt a clean technology to abate pollution.
The economic intuition of the Nash equilibrium outcomes of the ‘green’ versus sales delegation game can be carried out following the narrative of the cases detailed in Result 3. Because of the strategic interactions, the design of a standard SD contract to managers arises in equilibrium regardless of the weight the government places on the environmental damage. This is because of a twofold effect: (1) on the one hand, by including emissions in the compensation scheme managers tend to behave more aggressively at the pre-tax stage of the game, expanding output, reducing abatement and eventually gaining market share more with a delegation contract based on emissions instead of sales; (2) on the other hand, however, the optimal emissions tax levied by the government is higher under GD than under SD as managers tend to produce and pollute more if owners design a contract based on emissions instead of sales. The latter effect more than counterbalances the former so that the post-tax profits are larger in the symmetric GD scenario than in the symmetric SD scenario (irrespective of the value of $^g$![]() ).
).
In addition, as in the asymmetric scenario, the SD firm gets higher profits than the GD firm: SD is the dominant strategy of this game. We note that managers under SD abate more pollution than under GD and pay a lower amount of taxes. However, the SD manager produces more than the GD manager so that marginal costs under GD are smaller than under SD and the tax base tends to decrease in the latter case. Owners therefore will improve firms' profitability if they jointly deviate towards GD; in fact, by reducing output (and thus emissions), profits will increase, and as the percentage reduction in output gets lower, the percentage increases in the market price get higher. Therefore, by choosing the standard SD contract, owners are cast into a prisoner's dilemma and this result is policy-driven in the sense that emissions taxation is higher in the GD scenario than in the SD scenario due to the relative size of production and abatement in the two regimes.
We pinpoint here that, by changing the structure of the three games studied in sections 4–6 and considering the setting of the emissions fee occurring at the first stage (i.e., the regulator moves first), we avoid including the pre-play stage, which confirms the Nash equilibrium outcomes of the article except for the GD game, in which only (GD,GD) emerges as the unique Pareto-inefficient Nash equilibrium.
7. Discussion and concluding remarks
This article investigates the owners' decision of whether to delegate to managers the choice of pollution abatement in a Cournot duopoly with homogeneous goods and pollution externalities. It also assumes the existence of a government whose aim is to maximise social welfare using an emissions tax to incentivise firms to undertake emissions-reduction actions (Buccella et al., Reference Buccella, Fanti and Gori2021). In doing so, the work develops a three-stage non-cooperative game (solved by backward induction) augmented with a pre-play stage (or contract stage) during which firms choose whether to be delegated (with contracts based either on emissions or sales) or profit maximisers. Under this choice, first the government fixes the emissions tax, and then owners strategically choose whether to retain the choices of the abatement and output levels or delegate those decisions to a manager via an incentivising emissions contract or a standard sales contract, after having selected the optimal incentive at the bonus stage.
We summarize certain noteworthy findings. Comparing equilibrium profits, firms should prefer a contract based on an incentive weighting emissions instead of sales. Rather paradoxically, to have higher environmental quality, it is better to design a contract based on emissions. By contrast, employment, production and social welfare are favoured by a contract based on a weighted sum between profits and sales. Therefore, the article definitively pinpoints a well-known trade-off between employment and environmental quality emerging in the choice of managerial delegation contracts. The article also extends the GD game to include horizontal product differentiation, confirming that designing a managerial contract incentivising emissions can indeed allow us to achieve an equilibrium outcome working towards environmental protection if played against PM.
This work focuses on simplicity, as the models are based on a set of precise assumptions that call for further extensions. In this regard, a first line of research could be devoted to the study of different functional forms about demand and cost functions or the introduction of different government emissions tax schedules while also considering the issue of corporate social responsibility.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/S1355770X21000206.
Acknowledgements
The authors gratefully acknowledge the two anonymous reviewers for their valuable comments and suggestions thereby facilitating improvement in the quality of the work. The article was conceived when Domenico Buccella was Visiting Researcher at the Department of Law, University of Pisa, whose hospitality is gratefully acknowledged. Luciano Fanti acknowledges financial support from the University of Pisa under the ‘PRA – Progetti di Ricerca di Ateneo’ (Institutional Research Grants) – Project No. PRA_2018_12 ‘Institutions, imperfect markets and policy problems’. Luca Gori acknowledges financial support from the University of Pisa under the ‘PRA – Progetti di Ricerca di Ateneo’ (Institutional Research Grants) – Project No. PRA_2020_64 ‘Infectious diseases, health and development: economic and legal effects’. The usual disclaimer applies.
Financial support
The authors declare that this study was funded by the University of Pisa: grant No. PRA_2018_12 and grant No. PRA_2020_64.
Competing Interests
The authors declare none.
Informed consent
Informed consent was obtained from all participants included in the study.





