No CrossRef data available.
Article contents
Asymptotic distribution for pairs of linear and quadratic forms at integral vectors
Published online by Cambridge University Press: 17 April 2024
Abstract
We study the joint distribution of values of a pair consisting of a quadratic form 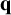 ${\mathbf q}$ and a linear form
${\mathbf q}$ and a linear form  ${\mathbf l}$ over the set of integral vectors, a problem initiated by Dani and Margulis [Orbit closures of generic unipotent flows on homogeneous spaces of
${\mathbf l}$ over the set of integral vectors, a problem initiated by Dani and Margulis [Orbit closures of generic unipotent flows on homogeneous spaces of  $\mathrm{SL}_3(\mathbb{R})$. Math. Ann. 286 (1990), 101–128]. In the spirit of the celebrated theorem of Eskin, Margulis and Mozes on the quantitative version of the Oppenheim conjecture, we show that if
$\mathrm{SL}_3(\mathbb{R})$. Math. Ann. 286 (1990), 101–128]. In the spirit of the celebrated theorem of Eskin, Margulis and Mozes on the quantitative version of the Oppenheim conjecture, we show that if 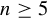 $n \ge 5$, then under the assumptions that for every
$n \ge 5$, then under the assumptions that for every 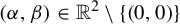 $(\alpha , \beta ) \in {\mathbb {R}}^2 \setminus \{ (0,0) \}$, the form
$(\alpha , \beta ) \in {\mathbb {R}}^2 \setminus \{ (0,0) \}$, the form 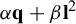 $\alpha {\mathbf q} + \beta {\mathbf l}^2$ is irrational and that the signature of the restriction of
$\alpha {\mathbf q} + \beta {\mathbf l}^2$ is irrational and that the signature of the restriction of 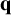 ${\mathbf q}$ to the kernel of
${\mathbf q}$ to the kernel of 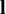 ${\mathbf l}$ is
${\mathbf l}$ is 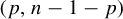 $(p, n-1-p)$, where
$(p, n-1-p)$, where 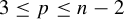 ${3\le p\le n-2}$, the number of vectors
${3\le p\le n-2}$, the number of vectors 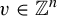 $v \in {\mathbb {Z}}^n$ for which
$v \in {\mathbb {Z}}^n$ for which  $\|v\| < T$,
$\|v\| < T$, 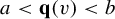 $a < {\mathbf q}(v) < b$ and
$a < {\mathbf q}(v) < b$ and 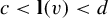 $c< {\mathbf l}(v) < d$ is asymptotically
$c< {\mathbf l}(v) < d$ is asymptotically 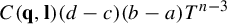 $ C({\mathbf q}, {\mathbf l})(d-c)(b-a)T^{n-3}$ as
$ C({\mathbf q}, {\mathbf l})(d-c)(b-a)T^{n-3}$ as 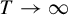 $T \to \infty $, where
$T \to \infty $, where 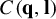 $C({\mathbf q}, {\mathbf l})$ only depends on
$C({\mathbf q}, {\mathbf l})$ only depends on 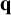 ${\mathbf q}$ and
${\mathbf q}$ and 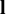 ${\mathbf l}$. The density of the set of joint values of
${\mathbf l}$. The density of the set of joint values of 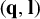 $({\mathbf q}, {\mathbf l})$ under the same assumptions is shown by Gorodnik [Oppenheim conjecture for pairs consisting of a linear form and a quadratic form. Trans. Amer. Math. Soc. 356(11) (2004), 4447–4463].
$({\mathbf q}, {\mathbf l})$ under the same assumptions is shown by Gorodnik [Oppenheim conjecture for pairs consisting of a linear form and a quadratic form. Trans. Amer. Math. Soc. 356(11) (2004), 4447–4463].
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press


