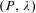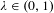Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gaivão, José Pedro
and
Nogueira, Arnaldo
2022.
Dynamics of piecewise increasing contractions.
Bulletin of the London Mathematical Society,
Vol. 54,
Issue. 2,
p.
482.
JAIN, SAKSHI
and
LIVERANI, CARLANGELO
2025.
Piecewise contractions.
Ergodic Theory and Dynamical Systems,
Vol. 45,
Issue. 5,
p.
1503.
Gaivão, José Pedro
Laurent, Michel
and
Nogueira, Arnaldo
2025.
Rotation number of 2-interval piecewise affine maps.
Aequationes mathematicae,
Vol. 99,
Issue. 2,
p.
511.
GAIVÃO, JOSÉ PEDRO
and
PIRES, BENITO
2025.
Multi-dimensional piecewise contractions are asymptotically periodic.
Ergodic Theory and Dynamical Systems,
p.
1.