Hostname: page-component-7dd5485656-npwhs Total loading time: 0 Render date: 2025-10-30T19:52:47.020Z Has data issue: false hasContentIssue false
  • English
  • Français

Classifying orbits of the affine group over the integers

Published online by Cambridge University Press:  22 July 2015

LEONARDO MANUEL CABRER  and
DANIELE MUNDICI
LEONARDO MANUEL CABRER
Affiliation:
Department of Statistics, Computer Science and Applications, ‘Giuseppe Parenti’, University of Florence, Viale Morgagni 59 – 50134, Florence, Italy email l.cabrer@disia.unifi.it
DANIELE MUNDICI
Affiliation:
Department of Mathematics and Computer Science ‘Ulisse Dini’, University of Florence, Viale Morgagni 67/A, I-50134 Florence, Italy email mundici@math.unifi.it
Get access Rights & Permissions [Opens in a new window]

Abstract

For each 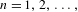$n=1,2,\ldots ,$ let 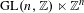$\text{GL}(n,\mathbb{Z})\ltimes \mathbb{Z}^{n}$ be the affine group over the integers. For every point 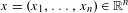$x=(x_{1},\ldots ,x_{n})\in \mathbb{R}^{n}$ let 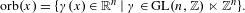$\text{orb}(x)=\{\unicode[STIX]{x1D6FE}(x)\in \mathbb{R}^{n}\mid \unicode[STIX]{x1D6FE}\in \text{GL}(n,\mathbb{Z})\ltimes \mathbb{Z}^{n}\}.$ Let 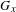$G_{x}$ be the subgroup of the additive group 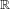$\mathbb{R}$ generated by 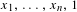$x_{1},\ldots ,x_{n},1$ . If 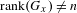$\text{rank}(G_{x})\neq n$ then 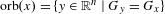$\text{orb}(x)=\{y\in \mathbb{R}^{n}\mid G_{y}=G_{x}\}$ . Thus, 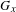$G_{x}$ is a complete classifier of 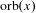$\text{orb}(x)$ . By contrast, if 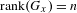$\text{rank}(G_{x})=n$ , knowledge of 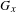$G_{x}$ alone is not sufficient in general to uniquely recover 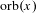$\text{orb}(x)$ ; as a matter of fact, 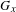$G_{x}$ determines precisely 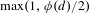$\max (1,\unicode[STIX]{x1D719}(d)/2)$ different orbits, where 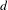$d$ is the denominator of the smallest positive non-zero rational in 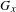$G_{x}$ and 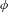$\unicode[STIX]{x1D719}$ is the Euler function. To get a complete classification, rational polyhedral geometry provides an integer 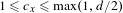$1\leq c_{x}\leq \max (1,d/2)$ such that 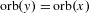$\text{orb}(y)=\text{orb}(x)$ if and only if 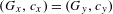$(G_{x},c_{x})=(G_{y},c_{y})$ . Applications are given to lattice-ordered abelian groups with strong unit and to AF 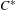$C^{\ast }$ -algebras.

Information

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 2 , April 2017 , pp. 440 - 453
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bigard, A., Keimel, K. and Wolfenstein, S.. Groupes et Anneaux Réticulés (Lecture Notes in Mathematics, 608) . Springer, Berlin, 1971.Google Scholar
Boca, F.. An AF algebra associated with the Farey tessellation. Canad. J. Math. 60 (2008), 975–1000.CrossRefGoogle Scholar
Dani, J. S.. Density properties of orbits under discrete groups. J. Indian Math. Soc. (N.S.) 39 (1975), 189–218.Google Scholar
Eckhardt, C.. A noncommutative Gauss map. Math. Scand. 108 (2011), 233–250.CrossRefGoogle Scholar
Effros, E. G.. Dimensions and C ∗ -Algebras (CBMS Regional Conference Series in Mathematics, 46) . American Mathematical Society, Providence, RI, 1981.CrossRefGoogle Scholar
Ewald, G.. Combinatorial Convexity and Algebraic Geometry (Graduate Texts in Mathematics, 168) . Springer, New York, 1996.CrossRefGoogle Scholar
Goodearl, K. R.. Notes on Real and Complex C ∗ -Algebras (Shiva Mathematics Series, 5) . Birkhäuser, Boston, 1982.Google Scholar
Guilloux, A.. A brief remark on orbits of SL(2, ℤ) in the Euclidean plane. Ergod. Th. & Dynam. Sys. 30 (2010), 1101–1109.CrossRefGoogle Scholar
Laurent, M. and Nogueira, A.. Approximation to points in the plane by SL(2, ℤ)-orbits. J. Lond. Math. Soc. (2) 85 (2012), 409–429.CrossRefGoogle Scholar
Mundici, D.. Interpretation of AF C ∗ -algebras in Łukasiewicz sentential calculus. J. Funct. Anal. 65 (1986), 15–63.CrossRefGoogle Scholar
Mundici, D.. Farey stellar subdivisions, ultrasimplicial groups, and K 0 of AF C ∗ -algebras. Adv. Math. 68 (1988), 23–39.CrossRefGoogle Scholar
Mundici, D.. The Haar theorem for lattice-ordered abelian groups with order-unit. Discrete Contin. Dyn. Syst. 21 (2008), 537–549.CrossRefGoogle Scholar
Mundici, D.. Revisiting the Farey AF algebra. Milan J. Math. 79 (2011), 643–656.CrossRefGoogle Scholar
Mundici, D.. Invariant measure under the affine group over ℤ. Combin. Probab. Comput. 23 (2014), 248–268.CrossRefGoogle Scholar
Nogueira, A.. Orbit distribution on ℝ2 under the natural action of SL(2, ℤ). Indag. Math. (N.S.) 13 (2002), 103–124.CrossRefGoogle Scholar
Nogueira, A.. Lattice orbit distribution on ℝ2 . Ergod. Th. & Dynam. Sys. 30 (2010), 1201–1214; Erratum, ibid., p. 1215.CrossRefGoogle Scholar
Witten, E.. SL(2, ℤ) action on three-dimensional conformal field theories with abelian symmetry. From Fields to Strings: Circumnavigating Theoretical Physics (Ian Kogan Memorial Collection, 3) . Ed. Shifman, M. et al. . World Scientific, Singapore, 2005, pp. 1173–1200.CrossRefGoogle Scholar