Article contents
Distribution of shapes of orthogonal lattices
Published online by Cambridge University Press: 02 November 2017
Abstract
It was recently shown by Aka, Einsiedler and Shapira that if 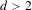 $d>2$, the set of primitive vectors on large spheres when projected to the
$d>2$, the set of primitive vectors on large spheres when projected to the 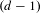 $(d-1)$-dimensional sphere coupled with the shape of the lattice in their orthogonal complement equidistribute in the product space of the sphere with the space of shapes of
$(d-1)$-dimensional sphere coupled with the shape of the lattice in their orthogonal complement equidistribute in the product space of the sphere with the space of shapes of 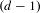 $(d-1)$-dimensional lattices. Specifically, for
$(d-1)$-dimensional lattices. Specifically, for 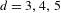 $d=3,4,5$ some congruence conditions are assumed. By using recent advances in the theory of unipotent flows, we effectivize the dynamical proof to remove those conditions for
$d=3,4,5$ some congruence conditions are assumed. By using recent advances in the theory of unipotent flows, we effectivize the dynamical proof to remove those conditions for 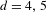 $d=4,5$. It also follows that equidistribution takes place with a polynomial error term with respect to the length of the primitive points.
$d=4,5$. It also follows that equidistribution takes place with a polynomial error term with respect to the length of the primitive points.
Information
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2017
References
- 7
- Cited by

