Article contents
Equivariant wrapped Floer homology and symmetric periodic Reeb orbits
Published online by Cambridge University Press: 04 February 2021
Abstract
The aim of this article is to apply a Floer theory to study symmetric periodic Reeb orbits. We define positive equivariant wrapped Floer homology using a (anti-)symplectic involution on a Liouville domain and investigate its algebraic properties. By a careful analysis of index iterations, we obtain a non-trivial lower bound on the minimal number of geometrically distinct symmetric periodic Reeb orbits on a certain class of real contact manifolds. This includes non-degenerate real dynamically convex star-shaped hypersurfaces in 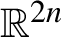 ${\mathbb {R}}^{2n}$ which are invariant under complex conjugation. As a result, we give a partial answer to the Seifert conjecture on brake orbits in the contact setting.
${\mathbb {R}}^{2n}$ which are invariant under complex conjugation. As a result, we give a partial answer to the Seifert conjecture on brake orbits in the contact setting.
Keywords
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 5
- Cited by


