Hostname: page-component-758b78586c-kdfvs Total loading time: 0 Render date: 2023-11-28T17:25:04.041Z Has data issue: false Feature Flags: { "corePageComponentGetUserInfoFromSharedSession": true, "coreDisableEcommerce": false, "useRatesEcommerce": true } hasContentIssue false
  • English
  • Français

Gibbs and equilibrium measures for some families of subshifts

Published online by Cambridge University Press:  16 May 2012

TOM MEYEROVITCH
TOM MEYEROVITCH*
Affiliation:
University of British Columbia, 1933 West Mall, Vancouver, British Columbia, Canada V6T1Z2 (email: tomm@math.ubc.ca)
Get access Rights & Permissions [Opens in a new window]

Abstract

For subshifts of finite type (SFTs), any equilibrium measure is Gibbs, as long as $f$ has 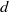$d$-summable variation. This is a theorem of Lanford and Ruelle. Conversely, a theorem of Dobrušin states that for strongly irreducible subshifts, shift-invariant Gibbs measures are equilibrium measures. Here we prove a generalization of the Lanford–Ruelle theorem: for all subshifts, any equilibrium measure for a function with 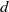$d$-summable variation is ‘topologically Gibbs’. This is a relaxed notion which coincides with the usual notion of a Gibbs measure for SFTs. In the second part of the paper, we study Gibbs and equilibrium measures for some interesting families of subshifts: 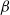$\beta $-shifts, Dyck shifts and Kalikow-type shifts (defined below). In all of these cases, a Lanford–Ruelle-type theorem holds. For each of these families, we provide a specific proof of the result.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 3 , June 2013 , pp. 934 - 953
Copyright
Copyright © 2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Aaronson, J. and Nakada, H.. Exchangeable, Gibbs and equilibrium measures for Markov subshifts. Ergod. Th. & Dynam. Sys. 27(2) (2007), 321–339.Google Scholar
[2]Bowen, R.. Some systems with unique equilibrium states. Math. Syst. Theory 8(3) (1974/75), 193–202.Google Scholar
[3]Burton, R. and Steif, J. E.. Non-uniqueness of measures of maximal entropy for subshifts of finite type. Ergod. Th. & Dynam. Sys. 14(2) (1994), 213–235.Google Scholar
[4]Dobrušin, R. L.. Gibbsian random fields for lattice systems with pairwise interactions. Funkcional. Anal. i Priložen. 2(4) (1968), 31–43.Google Scholar
[5]Feldman, J. and Moore, C. C.. Ergodic equivalence relations, cohomology, and von Neumann algebras. I. Trans. Amer. Math. Soc. 234(2) (1977), 289–324.Google Scholar
[6]Hamachi, T. and Inoue, K.. Embedding of shifts of finite type into the Dyck shift. Monatsh. Math. 145(2) (2005), 107–129.Google Scholar
[7]Kalikow, S. A.. $T, T^{-1}$ transformation is not loosely Bernoulli. Ann. of Math. (2) 115(2) (1982), 393–409.Google Scholar
[8]Krieger, W.. On the uniqueness of the equilibrium state. Math. Syst. Theory 8(2) (1974/75), 97–104.Google Scholar
[9]Krieger, W.. On dimension functions and topological Markov chains. Invent. Math. 56(3) (1980), 239–250.Google Scholar
[10]Krieger, W. and Matsumoto, K.. A lambda-graph system for the Dyck shift and its $K$-groups. Doc. Math. 8 (2003), 79–96 (electronic).Google Scholar
[11]Lanford, O. E. and Robinson, D. W.. Statistical mechanics of quantum spin systems. III. Comm. Math. Phys. 9 (1968), 327–338.Google Scholar
[12]Lanford, O. E. and Ruelle, D.. Observables at infinity and states with short range correlations in statistical mechanics. Comm. Math. Phys. 13 (1969), 194–215.Google Scholar
[13]Marcus, B. and Newhouse, S.. Measures of maximal entropy for a class of skew products. Ergodic Theory (Proc. Conf., Math. Forschungsinst., Oberwolfach, 1978) (Lecture Notes in Mathematics, 729). Springer, Berlin, 1979, pp. 105–125.Google Scholar
[14]Meyerovitch, T.. Tail invariant measures of the Dyck shift. Israel J. Math. 163 (2008), 61–83.Google Scholar
[15]Parry, W.. On the $\beta $-expansions of real numbers. Acta Math. Acad. Sci. Hungar. 11 (1960), 401–416.Google Scholar
[16]Petersen, K. and Schmidt, K.. Symmetric Gibbs measures. Trans. Amer. Math. Soc. 349(7) (1997), 2775–2811.Google Scholar
[17]Ruelle, D.. Thermodynamic Formalism, 2nd edn(Cambridge Mathematical Library). Cambridge University Press, Cambridge, 2004.Google Scholar
[18]Schmeling, J.. Symbolic dynamics for $\beta $-shifts and self-normal numbers. Ergod. Th. & Dynam. Sys. 17(3) (1997), 675–694.Google Scholar
[19]Schmidt, K.. Invariant cocycles, random tilings and the super-$K$ and strong Markov properties. Trans. Amer. Math. Soc. 349(7) (1997), 2813–2825.Google Scholar
[20]Schmidt, K.. Algebraic coding of expansive group automorphisms and two-sided beta-shifts. Monatsh. Math. 129(1) (2000), 37–61.Google Scholar
[21]Walters, P.. Ruelle’s operator theorem and $g$-measures. Trans. Amer. Math. Soc. 214 (1975), 375–387.Google Scholar
[22]Walters, P.. A variational principle for the pressure of continuous transformations. Amer. J. Math. 97(4) (1975), 937–971.Google Scholar
[23]Walters, P.. Equilibrium states for $\beta $-transformations and related transformations. Math. Z. 159(1) (1978), 65–88.Google Scholar