Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
Hostname: page-component-768dbb666b-t89mg Total loading time: 0.887 Render date: 2023-02-05T07:45:30.672Z Has data issue: true Feature Flags: { "useRatesEcommerce": false } hasContentIssue true
  • English
Ergodic Theory and Dynamical Systems Ergodic Theory and Dynamical Systems

Article contents

Hyperconvex representations and exponential growth

Published online by Cambridge University Press:  25 January 2013

A. SAMBARINO
A. SAMBARINO*
Affiliation:
Département de Mathématiques, Université Paris Sud, F-91405 Orsay, France email andres.sambarino@gmail.com
Get access Rights & Permissions[Opens in a new window]

Abstract

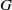Let $G$ be a real algebraic semi-simple Lie group and 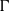$\Gamma $ be the fundamental group of a closed negatively curved manifold. In this article we study the limit cone, introduced by Benoist [Propriétés asymptotiques des groupes linéaires. Geom. Funct. Anal. 7(1) (1997), 1–47], and the growth indicator function, introduced by Quint [Divergence exponentielle des sous-groupes discrets en rang supérieur. Comment. Math. Helv. 77 (2002), 503–608], for a class of representations 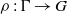$\rho : \Gamma \rightarrow G$ admitting an equivariant map from 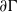$\partial \Gamma $ to the Furstenberg boundary of the symmetric space of 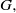$G, $ together with a transversality condition. We then study how these objects vary with the representation.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 3 , June 2014 , pp. 986 - 1010
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramov, L. M.. On the entropy of a flow. Dokl. Akad. Nauk SSSR 128 (1959), 873–875.Google Scholar
Akerkar, R.. Nonlinear Functional Analysis. Narosa Publishing House, 1999.Google Scholar
Barreira, L. and Pesin, Ya.. Lectures on Lyapunov exponents and smooth ergodic theory. Smooth Ergodic Theory and its Applications (Seattle, 1999) (Proc. Symp. in Pure Mathematics). American Mathematical Society, Providence, RI, 2000.Google Scholar
Benoist, Y.. Propriétés asymptotiques des groupes linéaires. Geom. Funct. Anal. 7 (1) (1997), 1–47.CrossRefGoogle Scholar
Benoist, Y.. Propriétés asymptotiques des groupes linéaires II. Adv. Stud. Pure Math. 26 (2000), 33–44.Google Scholar
Benoist, Y.. Convexes divisibles I. Algebraic Groups and Arithmetic. Tata Institute of Fundamental Research, 2004, pp. 339–374.Google Scholar
Bhatia, R. and Parthasarathy, K. R.. Lecture on Functional Analysis. MacMillan, Delhi, 1977.Google Scholar
Bowen, R.. Periodic orbits of hyperbolic flows. Amer. J. Math. 94 (1972), 1–30.CrossRefGoogle Scholar
Bowen, R.. Symbolic dynamics for hyperbolic flows. Amer. J. Math. 95 (1973), 429–460.CrossRefGoogle Scholar
Bowen, R. and Ruelle, D.. The ergodic theory of axiom A flows. Invent. Math. 29 (1975), 181–202.CrossRefGoogle Scholar
Guichard, O. and Wienhard, A.. Anosov representations: domains of discontinuity and applications. Invent. Math. 190 (2012), 357–438.CrossRefGoogle Scholar
Labourie, F.. Anosov flows, surface groups and curves in projective space. Invent. Math. 165 (2006), 51–114.CrossRefGoogle Scholar
Ledrappier, F.. Structure au bord des variétés à courbure négative. Sémin. Théor. Spectr. Géom. 71 (1994–1995), 97–122.Google Scholar
Livšic, A. N.. Cohomology of dynamical systems. Math. USSR Izv. 6 (1972), 1278–1301.CrossRefGoogle Scholar
Margulis, G.. Applications of ergodic theory to the investigation of manifolds with negative curvature. Funct. Anal. Appl. 3 (1969), 335–336.CrossRefGoogle Scholar
Patterson, S.-J.. The limit set of a Fuchsian group. Acta Math. 136 (1976), 241–273.CrossRefGoogle Scholar
Pollicott, M. and Sharp, R.. Length asymptotics in higher Teichmüller theory. Preprint, 2012.Google Scholar
Quint, J.-F.. Divergence exponentielle des sous-groupes discrets en rang supérieur. Comment. Math. Helv. 77 (2002), 503–608.CrossRefGoogle Scholar
Quint, J.-F.. Mesures de Patterson–Sullivan en rang supérieur. Geom. Funct. Anal. 12 (2002), 776–809.CrossRefGoogle Scholar
Quint, J.-F.. L’indicateur de croissance des groupes de Schottky. Ergod. Th. & Dynam. Sys. 23 (2003), 249–272.CrossRefGoogle Scholar
Ratner, M.. The central limit theorem for geodesic flows on $n$-manifolds of negative curvature. Israel J. Math. 16 (1973), 181–197.CrossRefGoogle Scholar
Ruelle, D.. Thermodynamic Formalism. Addison-Wesley, London, 1978.Google Scholar
Sambarino, A.. Quantitative properties of convex representations. Comm. Math. Helv., to appear, arXiv:1104.4705v1.Google Scholar
Shub, M.. Global Stability of Dynamical Systems. Springer, New York, 1987.CrossRefGoogle Scholar
Sullivan, D.. The density at infinity of a discrete group of hyperbolic motions. Publ. Math. Inst. Hautes Études Sci. 50 (1979), 171–202.CrossRefGoogle Scholar
Thirion, X.. Propriétés de mélange du flot des chambres de Weyl des groupes de Ping-Pong (Bulletin de la SMF, 137). Société mathématique de France, 2009, pp. 387–421.Google Scholar
Tits, J.. Représentations linéaires irréductibles d’un groupe réductif sur un corps quelconqe. J. Reine Angew. Math. 247 (1971), 196–220.Google Scholar
Yue, C.. The ergodic theory of discrete isometry groups on manifolds of variable negative curvature. Trans. Amer. Math. Soc. 348 (12) (1996), 4965–5005.CrossRefGoogle Scholar
10
Cited by

Save article to Kindle

To save this article to your Kindle, first ensure coreplatform@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Hyperconvex representations and exponential growth
Available formats
×

Save article to Dropbox

To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.

Hyperconvex representations and exponential growth
Available formats
×

Save article to Google Drive

To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.

Hyperconvex representations and exponential growth
Available formats
×
×

Reply to: Submit a response

Please enter your response.

Your details

Please enter a valid email address.

Conflicting interests

Do you have any conflicting interests? *