Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-27T02:48:27.736Z Has data issue: false hasContentIssue false
  • English
  • Français

Indiscriminate covers of infinite translation surfaces are innocent, not devious

Published online by Cambridge University Press:  04 December 2017

W. PATRICK HOOPER  and
RODRIGO TREVIÑO
W. PATRICK HOOPER
Affiliation:
The City College of New York, New York, NY 10031, USA CUNY Graduate Center, New York, NY 10016, USA email whooper@ccny.cuny.edu
RODRIGO TREVIÑO
Affiliation:
Department of Mathematics, University of Maryland, College Park, USA email rodrigo@math.umd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the interaction between passing to finite covers and ergodic properties of the straight-line flow on finite-area translation surfaces with infinite topological type. Infinite type provides for a rich family of degree-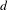$d$ covers for any integer $d>1$. We give examples which demonstrate that passing to a finite cover can destroy ergodicity, but we also provide evidence that this phenomenon is rare. We define a natural notion of a random degree 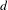$d$ cover and show that, in many cases, ergodicity and unique ergodicity are preserved under passing to random covers. This work provides a new context for exploring the relationship between recurrence of the Teichmüller flow and ergodic properties of the straight-line flow.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 8 , August 2019 , pp. 2071 - 2127
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beardon, A. F. and Maskit, B.. Limit points of Kleinian groups and finite sided fundamental polyhedra. Acta Math. 132 (1974), 1–12.Google Scholar
Bowman, J. P.. The complete family of Arnoux–Yoccoz surfaces. Geom. Dedicata 164(1) (2013), 113–130.Google Scholar
Bufetov, A. I.. Limit theorems for suspension flows over Vershik automorphisms. Russian Math. Surveys 68(5) (2013), 789–860.Google Scholar
Cheung, Y. and Eskin, A.. Unique ergodicity of translation flows. Partially Hyperbolic Dynamics, Laminations, and Teichmüller Flow. Selected Papers of the Workshop, Toronto, Ontario, Canada, January 2006 (Fields Institute Communications, 51) . Ed. Giovanni, F. et al. . American Mathematical Society, Providence, RI, 2007, pp. 213–221.Google Scholar
Chamanara, R., Gardiner, F. P. and Lakic, N.. A hyperelliptic realization of the horseshoe and baker maps. Ergod. Th. & Dynam. Sys. 26(6) (2006), 1749–1768.Google Scholar
Chamanara, R.. Affine automorphism groups of surfaces of infinite type. In the Tradition of Ahlfors and Bers, III (Contemporary Mathematics, 355) . American Mathematical Society, Providence, RI, 2004, pp. 123–145.Google Scholar
Degli Esposti, M., Del Magno, G. and Lenci, M.. An infinite step billiard. Nonlinearity 11(4) (1998), 991–1013.Google Scholar
Herrlich, F. and Randecker, A.. Notes on the veech group of the chamanara surface, Preprint, 2016, arXiv:1612.06877.Google Scholar
Hooper, W. P.. Immersions and the space of all translation structures, Preprint, 2013, arXiv:1310.5193.Google Scholar
Hooper, W. P.. The invariant measures of some infinite interval exchange maps. Geom. Topol. 19(4) (2015), 1895–2038.Google Scholar
Hooper, W. Patrick. Immersions and translation structures I: The space of structures on the pointed disk, Preprint, 2016, arXiv:1309.4795.Google Scholar
Hubbard, J. H.. Teichmüller Theory and Applications to Geometry, Topology, and Dynamics, Vol. 1: Teichmüller theory. Matrix Editions, Ithaca, NY, 2006.Google Scholar
Hubert, P. and Weiss, B.. Ergodicity for infinite periodic translation surfaces. Compos. Math. 149(8) (2013), 1364–1380 (in English).Google Scholar
Lindsey, K. and Treviño, R.. Infinite type flat surface models of ergodic systems. Discrete Contin. Dyn. Syst. 36(10) (2016), 5509–5553.Google Scholar
Masur, H.. Hausdorff dimension of the set of nonergodic foliations of a quadratic differential. Duke Math. J. 66(3) (1992), 387–442.Google Scholar
Masur, H. and Smillie, J.. Hausdorff dimension of sets of nonergodic measured foliations. Ann. of Math. (2) 134(3) (1991), 455–543.Google Scholar
Masur, H. and Tabachnikov, S.. Rational billiards and flat structures. Handbook of Dynamical Systems, Vol. 1A. North-Holland, Amsterdam, 2002, pp. 1015–1089.Google Scholar
Przytycki, P., Schmithüsen, G. and Valdez, F.. Veech groups of Loch Ness monsters. Ann. Inst. Fourier 61(2) (2011), 673–687 (in English).Google Scholar
Puder, D.. Primitive words, free factors and measure preservation. Israel J. Math. (2013), 1–49 (in English).Google Scholar
Radó, T.. Über den Begriff der Riemannschen Fläche. Acta Litt. Sci. Szeged 2 (1925), 101–121, 10.Google Scholar
Randecker, A.. Wild translation surfaces and infinite genus, Preprint, 2014, arXiv:1410.1501.Google Scholar
Richards, I.. On the classification of noncompact surfaces. Trans. Amer. Math. Soc. 106(2) (1963), 259–269.Google Scholar
Ryan, K.. Elephant Rocks. Grove Press, New York, 1997.Google Scholar
Thurston, W. P.. On the geometry and dynamics of diffeomorphisms of surfaces. Bull. Amer. Math. Soc. (N.S.) 19(2) (1988), 417–431.Google Scholar
Treviño, R.. On the ergodicity of flat surfaces of finite area. Geom. Funct. Anal. (2014), 1–27.Google Scholar
Treviño, R.. Flat surfaces, Bratteli diagrams, and unique ergodicity à la Masur. Israel J. Math. (2017), to appear, arXiv:1604.03572.Google Scholar
Troubetzkoy, S.. Billiards in infinite polygons. Nonlinearity 12(3) (1999), 513–524.Google Scholar
Veech, W. A.. Teichmüller curves in moduli space, Eisenstein series and an application to triangular billiards. Invent. Math. 97(3) (1989), 553–583.Google Scholar
Vere-Jones, D.. Ergodic properties of nonnegative matrices. II. Pacific J. Math. 26 (1968), 601–620.Google Scholar