Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
an Huef, Astrid
Kang, Sooran
and
Raeburn, Iain
2015.
Spatial realisations of KMS states on the C⁎-algebras of higher-rank graphs.
Journal of Mathematical Analysis and Applications,
Vol. 427,
Issue. 2,
p.
977.
Thomsen, Klaus
2016.
Operator Algebras and Applications.
Vol. 12,
Issue. ,
p.
277.
Christensen, Johannes
and
Thomsen, Klaus
2016.
Finite digraphs and KMS states.
Journal of Mathematical Analysis and Applications,
Vol. 433,
Issue. 2,
p.
1626.
an Huef, Astrid
and
Raeburn, Iain
2016.
Operator Algebras and Applications.
Vol. 12,
Issue. ,
p.
177.
Farsi, Carla
Gillaspy, Elizabeth
Kang, Sooran
and
Packer, Judith
2017.
Excursions in Harmonic Analysis, Volume 5.
p.
35.
an Huef, Astrid
Kang, Sooran
and
Raeburn, Iain
2017.
KMS States on the Operator Algebras of Reducible Higher-Rank Graphs.
Integral Equations and Operator Theory,
Vol. 88,
Issue. 1,
p.
91.
Robertson, David
Rout, James
and
Sims, Aidan
2018.
KMS States on Generalised Bunce–Deddens Algebras and their Toeplitz Extensions.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 41,
Issue. 1,
p.
123.
Laca, Marcelo
Raeburn, Iain
Ramagge, Jacqui
and
Whittaker, Michael F.
2018.
Equilibrium states on operator algebras associated to self-similar actions of groupoids on graphs.
Advances in Mathematics,
Vol. 331,
Issue. ,
p.
268.
Christensen, Johannes
2018.
Symmetries of the KMS Simplex.
Communications in Mathematical Physics,
Vol. 364,
Issue. 1,
p.
357.
Kakariadis, Evgenios T.A.
2020.
Equilibrium states and entropy theory for Nica-Pimsner algebras.
Advances in Mathematics,
Vol. 362,
Issue. ,
p.
106940.
Christensen, Johannes
2020.
KMS states on the Toeplitz algebras of higher-rank graphs.
Journal of Mathematical Analysis and Applications,
Vol. 485,
Issue. 2,
p.
123841.
Kakariadis, Evgenios T.A.
2020.
Applications of entropy of product systems: Higher-rank graphs.
Linear Algebra and its Applications,
Vol. 594,
Issue. ,
p.
124.
Kakariadis, Evgenios T.A.
2020.
Entropy theory for the parametrization of the equilibrium states of Pimsner algebras.
Journal of Geometry and Physics,
Vol. 155,
Issue. ,
p.
103794.
Brownlowe, Nathan
Laca, Marcelo
Robertson, Dave
and
Sims, Aidan
2020.
Reconstructing directed graphs from generalized gauge actions on their Toeplitz algebras.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 150,
Issue. 5,
p.
2632.
Christensen, Johannes
and
Vaes, Stefaan
2022.
KMS Spectra for Group Actions on Compact Spaces.
Communications in Mathematical Physics,
Vol. 390,
Issue. 3,
p.
1341.
Neagu, Robert
2024.
The admissible KMS bundles on classifiable C⁎-algebras.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
p.
1.
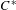 $C^{\ast }$-algebras of reducible graphs
$C^{\ast }$-algebras of reducible graphs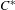 $C^{\ast }$-algebras of finite graphs obtained by lifting the gauge action to an action of the real line. Enomoto, Fujii and Watatani [KMS states for gauge action on
$C^{\ast }$-algebras of finite graphs obtained by lifting the gauge action to an action of the real line. Enomoto, Fujii and Watatani [KMS states for gauge action on 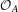 ${\mathcal{O}}_{A}$. Math. Japon.29 (1984), 607–619] proved that if the vertex matrix of the graph is irreducible, then the dynamics on the graph algebra admits a single Kubo–Martin–Schwinger (KMS) state. We have previously studied the dynamics on the Toeplitz algebra, and explicitly described a finite-dimensional simplex of KMS states for inverse temperatures above a critical value. Here we study the KMS states for graphs with reducible vertex matrix, and for inverse temperatures at and below the critical value. We prove a general result which describes all the KMS states at a fixed inverse temperature, and then apply this theorem to a variety of examples. We find that there can be many patterns of phase transition, depending on the behaviour of paths in the underlying graph.
${\mathcal{O}}_{A}$. Math. Japon.29 (1984), 607–619] proved that if the vertex matrix of the graph is irreducible, then the dynamics on the graph algebra admits a single Kubo–Martin–Schwinger (KMS) state. We have previously studied the dynamics on the Toeplitz algebra, and explicitly described a finite-dimensional simplex of KMS states for inverse temperatures above a critical value. Here we study the KMS states for graphs with reducible vertex matrix, and for inverse temperatures at and below the critical value. We prove a general result which describes all the KMS states at a fixed inverse temperature, and then apply this theorem to a variety of examples. We find that there can be many patterns of phase transition, depending on the behaviour of paths in the underlying graph.
