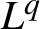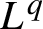Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Feng, De-Jun
and
Simon, Károly
2021.
Thermodynamic Formalism.
Vol. 2290,
Issue. ,
p.
421.
FENG, DE-JUN
and
SIMON, KÁROLY
2022.
Dimension estimates for iterated function systems and repellers. Part II.
Ergodic Theory and Dynamical Systems,
Vol. 42,
Issue. 11,
p.
3357.
Kolossváry, István
2023.
The Lq$L^q$ spectrum of self‐affine measures on sponges.
Journal of the London Mathematical Society,
Vol. 108,
Issue. 2,
p.
666.
Qiu, Hua
Wang, Qi
and
Wang, Shufang
2024.
L
q
-spectra of graph-directed planar non-conformal measures.
Nonlinearity,
Vol. 37,
Issue. 9,
p.
095003.