Hostname: page-component-7dd5485656-k8lnt Total loading time: 0 Render date: 2025-10-29T19:42:48.836Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixing sets, positive entropy homeomorphisms and non-Suslinean continua

Published online by Cambridge University Press:  01 June 2015

CHRISTOPHER MOURON
CHRISTOPHER MOURON*
Affiliation:
Department of Mathematics and Computer Science, Rhodes College, Memphis, TN 38112, USA email mouronc@rhodes.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 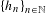$\{h_{n}\}_{n\in \mathbb{N}}$ be a sequence of self maps on a metric space 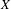$X$ . We say that 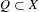$Q\subset X$ is a mixing set on 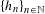$\{h_{n}\}_{n\in \mathbb{N}}$ if for every 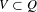$V\subset Q$ such that 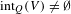$\text{int}_{Q}(V)\not =\emptyset$ and every 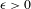$\unicode[STIX]{x1D716}>0$ there exists 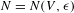$N=N(V,\unicode[STIX]{x1D716})$ such that 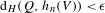$\text{d}_{H}(Q,h_{n}(V))<\unicode[STIX]{x1D716}$ for all 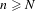$n\geq N$ , where 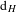$\text{d}_{H}$ is the Hausdorff metric. It is shown that if 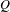$Q$ is a non-degenerate mixing set for a sequence of homeomorphisms on a continuum, then the continuum must be non-Suslinean. This is generalized to the notion of a 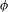$\unicode[STIX]{x1D719}$ -mixing set. As a corollary, it is shown that a continuum must be non-Suslinean in order to admit a positive entropy homeomorphism.

Information

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 7 , October 2016 , pp. 2246 - 2257
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adler, R. L. and McAndrew, M. H. . The entropy of Chebyshev polynomials. Trans. Amer. Math. Soc. 121(1) (1966), 236–241.Google Scholar
Kato, H.. Continuum-wise expansive homeomorphisms. Canad. J. Math. 45(3) (1993), 576–598.Google Scholar
Kerr, D. and Li, H.. Independence in topological and C ∗ -dynamics. Math. Ann. 338 (2007), 869–926.Google Scholar
Mouron, C.. The topology of continua that are approximated by disjoint subcontinua. Topology Appl. 156(3) (2009), 558–576.Google Scholar
Mouron, C.. Positive entropy homeomorphisms of chainable continua and indecomposable subcontinua. Proc. Amer. Math. Soc. 139(8) (2011), 2783–2791.Google Scholar
Nadler, S. B. Jr. Hyperspaces of Sets. A Text with Research Questions (Monographs and Textbooks in Pure and Applied Mathematics, 49) . Marcel Dekker, New York, 1978.Google Scholar
Seidler, G. T.. The topological entropy of homeomorphisms on one-dimensional continua. Proc. Amer. Math. Soc. 4 (1990), 1025–1030.Google Scholar
Walters, P.. A Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.Google Scholar