Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Yin, Zheng
and
Chen, Ercai
2016.
Large-deviation properties in some non-uniformly hyperbolic systems via Pesin theory.
Dynamical Systems,
Vol. 31,
Issue. 4,
p.
483.
Yin, Zheng
and
Chen, Ercai
2016.
Conditional variational principle for the irregular set in some nonuniformly hyperbolic systems.
Discrete and Continuous Dynamical Systems,
Vol. 36,
Issue. 11,
p.
6581.
VARANDAS, PAULO
and
ZHAO, YUN
2017.
Weak Gibbs measures: speed of convergence to entropy, topological and geometrical aspects.
Ergodic Theory and Dynamical Systems,
Vol. 37,
Issue. 7,
p.
2313.
Tian, Xueting
and
Varandas, Paulo
2017.
Topological entropy of level sets of empirical measures for non-uniformly expanding maps.
Discrete & Continuous Dynamical Systems - A,
Vol. 37,
Issue. 10,
p.
5407.
Pfister, C-E
and
Sullivan, W G
2018.
Weak Gibbs measures and large deviations.
Nonlinearity,
Vol. 31,
Issue. 1,
p.
49.
Bomfim, Thiago
and
Castro, Armando
2019.
Linear Response, and Consequences for Differentiability of Statistical Quantities and Multifractal Analysis.
Journal of Statistical Physics,
Vol. 174,
Issue. 1,
p.
135.
Bomfim, Thiago
and
Varandas, Paulo
2019.
The gluing orbit property, uniform hyperbolicity and large deviations principles for semiflows.
Journal of Differential Equations,
Vol. 267,
Issue. 1,
p.
228.
Ferreira, G.
2019.
The asymptotically additive topological pressure: variational principle for non-compact and intersection of irregular sets.
Dynamical Systems,
Vol. 34,
Issue. 3,
p.
484.
Climenhaga, Vaughn
and
Thompson, Daniel J.
2021.
Thermodynamic Formalism.
Vol. 2290,
Issue. ,
p.
3.
Nakano, Yushi
and
Zelerowicz, Agnieszka
2021.
Highly irregular orbits for subshifts of finite type: large intersections and emergence.
Nonlinearity,
Vol. 34,
Issue. 11,
p.
7609.
Araujo, V.
and
Pinheiro, V.
2021.
Abundance of Wild Historic Behavior.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 52,
Issue. 1,
p.
41.
NAKANO, Yushi
and
YAMAMOTO, Kenichiro
2021.
Irregular Sets for Piecewise Monotonic Maps.
Tokyo Journal of Mathematics,
Vol. 44,
Issue. 2,
Ji, Yong
Chen, Ercai
and
Lin, Zijie
2022.
High pointwise emergence and Katok’s conjecture for symbolic systems with non-uniform structure.
Nonlinearity,
Vol. 35,
Issue. 10,
p.
5226.
Ji, Yong
Chen, Ercai
and
Zhou, Xiaoyao
2022.
Packing Entropy of Saturated Sets for Nonuniformly Hyperbolic Systems.
International Journal of Bifurcation and Chaos,
Vol. 32,
Issue. 11,
Kiriki, Shin
Nakano, Yushi
and
Soma, Teruhiko
2022.
Emergence via non-existence of averages.
Advances in Mathematics,
Vol. 400,
Issue. ,
p.
108254.
Ren, Xiankun
Tian, Xueting
and
Zhou, Yunhua
2023.
On the Topological Entropy of Saturated Sets for Amenable Group Actions.
Journal of Dynamics and Differential Equations,
Vol. 35,
Issue. 4,
p.
2873.
Attia, Najmeddine
and
Moulahi, Taoufik
2025.
Multifractal Structure of Irregular Sets via Weighted Random Sequences.
Fractal and Fractional,
Vol. 9,
Issue. 12,
p.
793.
Zelerowicz, Agnieszka
2025.
Emergence for diffeomorphisms with nonzero Lyapunov exponents.
Nonlinearity,
Vol. 38,
Issue. 10,
p.
105001.
 $f$ has an expanding repeller and
$f$ has an expanding repeller and 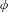 $\unicode[STIX]{x1D719}$ is a Hölder continuous potential, we prove that the topological pressure of the set of points whose accumulation values of Birkhoff averages belong to some interval
$\unicode[STIX]{x1D719}$ is a Hölder continuous potential, we prove that the topological pressure of the set of points whose accumulation values of Birkhoff averages belong to some interval 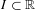 $I\subset \mathbb{R}$ can be expressed in terms of the topological pressure of the whole system and the large deviations rate function. As a byproduct we deduce that most irregular sets for maps with the specification property have topological pressure strictly smaller than the whole system. Some extensions to a non-uniformly hyperbolic setting, level-2 irregular sets and hyperbolic flows are also given.
$I\subset \mathbb{R}$ can be expressed in terms of the topological pressure of the whole system and the large deviations rate function. As a byproduct we deduce that most irregular sets for maps with the specification property have topological pressure strictly smaller than the whole system. Some extensions to a non-uniformly hyperbolic setting, level-2 irregular sets and hyperbolic flows are also given.
