No CrossRef data available.
Article contents
On intrinsic ergodicity of factors of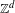 
$\mathbb{Z}^{d}$ subshifts
Published online by Cambridge University Press: 06 October 2015
Abstract
It is well known that any 
$\mathbb{Z}$ subshift with the specification property has the property that every factor is intrinsically ergodic, i.e. every factor has a unique factor of maximal entropy. In recent work, other 
$\mathbb{Z}$ subshifts have been shown to possess this property as well, including 
$\unicode[STIX]{x1D6FD}$ -shifts and a class of 
$S$ -gap shifts. We give two results that show that the situation for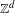 
$\mathbb{Z}^{d}$ subshifts with 
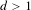$d>1$ is quite different. First, for any 
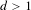$d>1$ , we show that any 
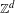$\mathbb{Z}^{d}$ subshift possessing a certain mixing property must have a factor with positive entropy which is not intrinsically ergodic. In particular, this shows that for 
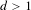$d>1$ , 
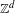$\mathbb{Z}^{d}$ subshifts with specification cannot have all factors intrinsically ergodic. We also give an example of a 
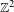$\mathbb{Z}^{2}$ shift of finite type, introduced by Hochman, which is not even topologically mixing, but for which every positive-entropy subshift factor is intrinsically ergodic.
Information
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2015
References
Bowen, R.. Some systems with unique equilibrium states. Math. Syst. Theory
8 (1974), 193–202.Google Scholar
Boyle, M.. Open problems in symbolic dynamics. Contemp. Math.
469 (2008), 69–118.CrossRefGoogle Scholar
Boyle, M., Pavlov, R. and Schraudner, M.. Multidimensional sofic shifts without separation and their factors. Trans. Amer. Math. Soc.
362 (2010), 4617–4653.Google Scholar
Burton, R. and Steif, J.. Non-uniqueness of measures of maximal entropy for subshifts of finite type. Ergod. Th. & Dynam. Sys.
14(2) (1994), 213–235.Google Scholar
Climenhaga, V. and Thompson, D.. Intrinsic ergodicity beyond specification: 𝛽-shifts, S-gap shifts, and their factors. Israel J. Math.
192(2) (2012), 785–817.Google Scholar
Cover, T. and Thomas, J.. Elements of Information Theory. John Wiley and Sons, New York, 2012.Google Scholar
Hochman, M.. On the automorphism groups of multidimensional SFTs. Ergod. Th. & Dynam. Sys.
30(3) (2010), 809–840.CrossRefGoogle Scholar
Lebowitz, J. and Gallavotti, G.. Phase transitions in binary lattice gases. J. Math. Phys.
12(7) (1971), 1129–1133.Google Scholar
Lind, D. and Marcus, B.. Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.Google Scholar
Misiurewicz, M.. A short proof of the variational principle for a ℤ+
n
-action on a compact space. Astérisque
40 (1975), 147–157.Google Scholar
Mozes, S.. Tilings, substitution systems and dynamical systems generated by them. J. Anal. Math.
53 (1989), 139–186.CrossRefGoogle Scholar
Radin, C.. Disordered ground states of classical lattice models. Rev. Math. Phys.
3 (1991), 125–135.Google Scholar
Robinson, R. M.. Undecidability and non-periodicity of tilings of the plane. Invent. Math.
12 (1971), 177–209.Google Scholar
Weiss, B.. Intrinsically ergodic systems. Bull. Amer. Math. Soc.
76(6) (1970), 1266–1269.CrossRefGoogle Scholar
Whittington, S. G. and Soteros, C. E.. Lattice animals: rigorous results and wild guesses. Disorder in Physical Systems
(Oxford Science Publications)
. Eds. Grimmett, G. R. and Welsh, D. J. A.. Oxford University Press, New York, 1990, pp. 323–335.Google Scholar
Widom, B. and Rowlinson, J. S.. New model for the study of liquid–vapor phase transitions. J. Chem. Phys.
52 (1970), 1670–1684.Google Scholar