Hostname: page-component-848d4c4894-p2v8j Total loading time: 0 Render date: 2024-04-30T20:10:39.454Z Has data issue: false hasContentIssue false
  • English
  • Français

On the irregular points for systems with the shadowing property

Published online by Cambridge University Press:  14 March 2017

YIWEI DONG ,
PIOTR OPROCHA  and
XUETING TIAN
YIWEI DONG
Affiliation:
School of Mathematical Science, Fudan University, Shanghai 200433, PR China email yiweidong@fudan.edu.cn, xuetingtian@fudan.edu.cn
PIOTR OPROCHA
Affiliation:
AGH University of Science and Technology, Faculty of Applied Mathematics, al. A. Mickiewicza 30, 30-059 Kraków, Poland National Supercomputing Centre IT4Innovations, Division of the University of Ostrava, Institute for Research and Applications of Fuzzy Modeling, 30 dubna 22, 70103 Ostrava, Czech Republic email oprocha@agh.edu.pl
XUETING TIAN
Affiliation:
School of Mathematical Science, Fudan University, Shanghai 200433, PR China email yiweidong@fudan.edu.cn, xuetingtian@fudan.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

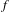We prove that when $f$ is a continuous self-map acting on a compact metric space 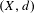$(X,d)$ that satisfies the shadowing property, then the set of irregular points (i.e., points with divergent Birkhoff averages) has full entropy. Using this fact, we prove that, in the class of 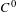$C^{0}$-generic maps on manifolds, we can only observe (in the sense of Lebesgue measure) points with convergent Birkhoff averages. In particular, the time average of atomic measures along orbits of such points converges to some Sinai–Ruelle–Bowen-like measure in the weak$^{\ast }$ topology. Moreover, such points carry zero entropy. In contrast, irregular points are non-observable but carry infinite entropy.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 6 , September 2018 , pp. 2108 - 2131
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdenur, F. and Andersson, M.. Ergodic theory of generic continuous maps. Comm. Math. Phys. 318 (2013), 831–855.Google Scholar
Adler, R. L., Konheim, A. G. and McAndrew, M. H.. Topological entropy. Trans. Amer. Math. Soc. 114 (1965), 309–319.Google Scholar
Akin, E. and Kolyada, S.. Li–Yorke sensitivity. Nonlinearity 16 (2003), 1421–1433.Google Scholar
Barreira, L. and Schmeling, J.. Sets of non-typical points have full topological entropy and full Hausdorff dimension. Israel J. Math. 116 (2000), 29–70.Google Scholar
Bing, R. H.. An alternative proof that 3-manifolds can be triangulated. Ann. of Math. (2) 69 (1959), 37–65.Google Scholar
Bowen, R.. Periodic points and measures for Axiom A diffeomorphisms. Trans. Amer. Math. Soc. 154 (1971), 377–397.Google Scholar
Bowen, R.. Entropy for group endomorphisms and homogeneous spaces. Trans. Amer. Math. Soc. 153 (1971), 401–414.Google Scholar
Bowen, R.. Topological entropy for noncompact sets. Trans. Amer. Math. Soc. 184 (1973), 125–136.Google Scholar
Brown, J. R.. Ergodic Theory and Topological Dynamics (Pure and Applied Mathematics, 70) . Academic Press, New York, 1976.Google Scholar
Buzzi, J.. Specification on the interval. Trans. Amer. Math. Soc. 349 (1997), 2737–2754.Google Scholar
Cairns, S. S.. Triangulation of the manifold of class one. Bull. Amer. Math. Soc. 41 (1935), 549–552.Google Scholar
Catsigeras, E. and Enrich, H.. SRB-like measures for C 0 dynamics. Bull. Pol. Acad. Sci. Math. 59 (2011), 151–164.Google Scholar
Che, L. and Li, S.. Shadowing property for inverse limit spaces. Proc. Amer. Math. Soc. 115 (1992), 573–580.Google Scholar
Chen, E., Tassilo, K. and Shu, L.. Topological entropy for divergence points. Ergod. Th. & Dynam. Sys. 25 (2005), 1173–1208.Google Scholar
Denker, M., Grillenberger, C. and Sigmund, K.. Ergodic Theory on the Compact Spaces (Lecture Notes in Mathematics, 527) . Springer, Berlin, 1976.Google Scholar
Downarowicz, T.. Survey of odometers and Toeplitz flows. Algebraic and Topological Dynamics (Contemporary Mathematics, 385) . American Mathematical Society, Providence, RI, 2005, pp. 7–37.Google Scholar
Falniowski, F., Kulczycki, M., Kwietniak, D. and Li, J.. Two results on entropy, chaos and independence in symbolic dynamics. Discrete Contin. Dyn. Syst. Ser. B 20 (2015), 3487–3505.Google Scholar
Fan, A., Feng, D. and Wu, J.. Recurrence, dimensions and entropy. J. Lond. Math. Soc. (2) 64 (2001), 229–244.Google Scholar
Katok, A.. Lyapunov exponents, entropy and periodic orbits for diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 51 (1980), 137–174.Google Scholar
Kirby, R. C. and Siebenmann, L. C.. On the triangulation of manifolds and the Hauptvermutung. Bull. Amer. Math. Soc. 75 (1969), 742–749.Google Scholar
Kościelniak, P.. On genericity of shadowing and periodic shadowing property. J. Math. Anal. Appl. 310 (2005), 188–196.Google Scholar
Kościelniak, P.. On the genericity of chaos. Topology Appl. 154 (2007), 1951–1955.Google Scholar
Kościelniak, P., Mazur, M., Oprocha, P. and Pilarczyk, P.. Shadowing is generic-a continuous case. Discrete Contin. Dyn. Syst. 34 (2014), 3591–3609.Google Scholar
Kulczycki, M., Kwietniak, D. and Oprocha, P.. On almost specification and average shadowing properties. Fund. Math. 224 (2014), 241–278.Google Scholar
Kurka, P.. Topological and Symbolic Dynamics (Cours Spécialisés [Specialized Courses], 11) . Société Mathématique de France, Paris, 2003.Google Scholar
Kwietniak, D., Łącka, M. and Oprocha, P.. A Panorama of Specification-like Properties and their Consequences (Dynamics and Numbers, Contemporary Mathematics, 669) . American Mathematical Society, Providence, RI, 2016, pp. 155–186.Google Scholar
Li, J. and Oprocha, P.. Shadowing property, weak mixing and regular recurrence. J. Dynam. Differential Equations 25 (2013), 1233–1249.Google Scholar
Li, J. and Wu, M.. Generic property of irregular sets in systems satisfying the specification property. Discrete Contin. Dyn. Syst. 34 (2014), 635–645.Google Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.Google Scholar
Moise, E. E.. Geometric Topology in Dimensions 2 and 3. Springer, New York, 1977.Google Scholar
Moothathu, T. K. S. and Oprocha, P.. Shadowing, entropy and minimal subsystems. Monatsh. Math. 172 (2013), 357–378.Google Scholar
Olsen, L.. Divergence points of deformed empirical measures. Math. Res. Lett. 9 (2002), 701–713.Google Scholar
Olsen, L.. Multifractal analysis of divergence points of deformed measure theoretical Birkhoff averages. J. Math. Pures Appl. 82 (2003), 1591–1649.Google Scholar
Olsen, L. and Winter, S.. Normal and non-normal points of self-similar sets and divergence points of self-similar measures. J. Lond. Math. Soc. 67 (2003), 103–122.Google Scholar
Pesin, Y.. Dimension Theory in Dynamical Systems (Contemporary Views and Applications) . University of Chicago Press, Chicago, 1997.Google Scholar
Pfister, C. E. and Sullivan, W. G.. Large deviations estimates for dynamical systems without the specification property. Application to the 𝛽-shifts. Nonlinearity 18 (2005), 237–261.Google Scholar
Pfister, C. E. and Sullivan, W. G.. On the topological entropy of saturated sets. Ergod. Th. & Dynam. Sys. 27 (2007), 929–956.Google Scholar
Pilyugin, S. Yu. and Plamenevskaya, O. B.. Shadowing is generic. Topology Appl. 97 (1999), 253–266.Google Scholar
Schmeling, J.. Symbolic dynamics for 𝛽-shifts and self-normal numbers. Ergod. Th. & Dynam. Sys. 17 (1997), 675–694.Google Scholar
Takens, F. and Verbitskiy, E.. On the variational principle for the topological entropy of certain non-compact sets. Ergod. Th. & Dynam. Sys. 23(1) (2003), 317–348.Google Scholar
Thompson, D. J.. Irregular sets, the 𝛽-transformation and the almost specification property. Trans. Amer. Math. Soc. 364 (2012), 5395–5414.Google Scholar
Walters, P.. An Introduction to Ergodic Theory. Springer, Berlin, 2001.Google Scholar
Walters, P.. On the pseudo-orbit tracing property and its relationship to stability. The Structure of Attractors in Dynamical Systems (Proc. Conf., North Dakota State University, Fargo, ND, 1977) (Lecture Notes in Mathematics, 668) . Springer, Berlin, 1978, pp. 231–244.Google Scholar
Whitehead, J. H. C.. On C 1 -complexes. Ann. of Math. (2) 41 (1940), 809–824.Google Scholar
Yano, K.. A remark on the topological entropy of homeomorphisms. Invent. Math. 59 (1980), 215–220.Google Scholar