In this paper, we make partial progress on a function field version of the dynamical uniform boundedness conjecture for certain one-dimensional families 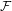${\mathcal{F}}$ of polynomial maps, such as the family 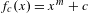$f_{c}(x)=x^{m}+c$, where 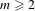$m\geq 2$. We do this by making use of the dynatomic modular curves 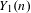$Y_{1}(n)$ (respectively 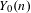$Y_{0}(n)$) which parametrize maps 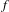$f$ in 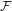${\mathcal{F}}$ together with a point (respectively orbit) of period $n$ for 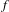$f$. The key point in our strategy is to study the set of primes 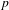$p$ for which the reduction of 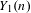$Y_{1}(n)$ modulo 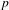$p$ fails to be smooth or irreducible. 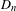Morton gave an algorithm to construct, for each $n$, a discriminant $D_{n}$ whose list of prime factors contains all the primes of bad reduction for 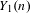$Y_{1}(n)$. In this paper, we refine and strengthen Morton’s results. Specifically, we exhibit two criteria on a prime 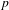$p$ dividing 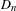$D_{n}$: one guarantees that 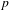$p$ is in fact a prime of bad reduction for 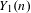$Y_{1}(n)$, yet this same criterion implies that 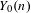$Y_{0}(n)$ is geometrically irreducible. The other guarantees that the reduction of 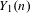$Y_{1}(n)$ modulo 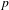$p$ is actually smooth. As an application of the second criterion, we extend results of Morton, Flynn, Poonen, Schaefer, and Stoll by giving new examples of good reduction of 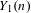$Y_{1}(n)$ for several primes dividing 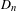$D_{n}$ when 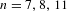$n=7,8,11$, and 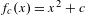$f_{c}(x)=x^{2}+c$. The proofs involve a blend of arithmetic and complex dynamics, reduction theory for curves, ramification theory, and the combinatorics of the Mandelbrot set.