Article contents
The Toeplitz noncommutative solenoid and its Kubo–Martin–Schwinger states
Published online by Cambridge University Press: 03 April 2017
Abstract
We use Katsura’s topological graphs to define Toeplitz extensions of Latrémolière and Packer’s noncommutative-solenoid 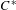 $C^{\ast }$-algebras. We identify a natural dynamics on each Toeplitz noncommutative solenoid and study the associated Kubo–Martin–Schwinger (KMS) states. Our main result shows that the space of extreme points of the KMS simplex of the Toeplitz noncommutative torus at a strictly positive inverse temperature is homeomorphic to a solenoid; indeed, there is an action of the solenoid group on the Toeplitz noncommutative solenoid that induces a free and transitive action on the extreme boundary of the KMS simplex. With the exception of the degenerate case of trivial rotations, at inverse temperature zero there is a unique KMS state, and only this one factors through Latrémolière and Packer’s noncommutative solenoid.
$C^{\ast }$-algebras. We identify a natural dynamics on each Toeplitz noncommutative solenoid and study the associated Kubo–Martin–Schwinger (KMS) states. Our main result shows that the space of extreme points of the KMS simplex of the Toeplitz noncommutative torus at a strictly positive inverse temperature is homeomorphic to a solenoid; indeed, there is an action of the solenoid group on the Toeplitz noncommutative solenoid that induces a free and transitive action on the extreme boundary of the KMS simplex. With the exception of the degenerate case of trivial rotations, at inverse temperature zero there is a unique KMS state, and only this one factors through Latrémolière and Packer’s noncommutative solenoid.
Information
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2017
References
A correction has been issued for this article:
- 5
- Cited by
Linked content
Please note a has been issued for this article.

