Hostname: page-component-6766d58669-7fx5l Total loading time: 0 Render date: 2026-05-22T09:01:57.129Z Has data issue: false hasContentIssue false
  • English
  • Français

Accumulation theorems for quadratic polynomials

Published online by Cambridge University Press:  19 September 2008

Dan Erik Krarup Sørensen
Dan Erik Krarup Sørensen
Affiliation:
Matematisk Institut, Bygn. 303, Danmarks Tekniske Universitet, DK-2800 Lyngby, Danmark (e-mail: dan@mat.dtu.dk)
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the one-parameter family of quadratic polynomials:

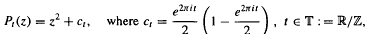
i.e. monic centered quadratic polynomials with an indifferent fixed point αt and prefixed point −αt. Let At, be any one of the sets {0, ±αt}, {±αt}, {0, αt}, or {0, −αt}. Then we prove that for quadratic Julia sets corresponding to a Gδ-dense subset of 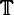there is an explicitly given external ray accumulating on At. In the case At = {±αt} the theorem is known as the Douady accumulation theorem.

Corollaries are the non-local connectivity of these Julia sets and the fact that all such Julia sets contain a Cremer point. Existence of non-locally connected quadratic Julia sets of Hausdorff dimension two is derived by using a recent result of Shishikura. By tuning, the results hold on the boundary of any hyperbolic component of the Mandelbrot set.

Finally, we concentrate on quadratic Cremer point polynomials. Here we prove that any ray accumulating on two symmetrical points of the Julia set must accumulate the origin. As a consequence, the dense Gδsets arising from the first two possible choices of At are the same. We also prove that, if two distinct rays accumulate both to two distinct points, then the rays must accumulate on a common continuum joining the two points. This supports the conjecture that αt and –αt may be joined by an arc in the Julia set.

Information

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 16 , Issue 3 , June 1996 , pp. 555 - 590
Copyright
Copyright © Cambridge University Press 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[Ah]Ahlfors, L. V.. Complex Analysis. Third Edn. McGraw-Hill, New York, 1979.Google Scholar
[At]Atela, P.. Bifurcations of dynamic rays in complex polynomials of degree two. Ergod. Th. & Dynam. Sys. 12 (1991), 401–423.CrossRefGoogle Scholar
[Br]Branner, B.. The Mandelbrot set. Proc. Symposia in Applied Math., AMS. 39 (1989), 75–105.CrossRefGoogle Scholar
[Bl]Blanchard, P.. Complex analytic dynamics on the Riemann sphere. Bull. Amer. Math. Soc. 11 (1985), 85–141.CrossRefGoogle Scholar
[BS]Bullett, S. and Sentenac, P.. Ordered orbits of the shift, square roots, and the devil's staircase. Math. Proc. Camb. Phil. Soc. 115 (1994), 451–481.CrossRefGoogle Scholar
[DD]Douady, A. and Douady, R.. Algébre et theories galoisiennes 2/théories galoisiennes. Cedic/Fernand Nathan, Paris, 1979.Google Scholar
[DH1]Douady, A. and Hubbard, J. H.. Étude dynamique des polynômes complexes I-II (also referred to as the Orsay notes). Publications Mathematiques d'Orsuy. (1984).Google Scholar
[DH2]Douady, A. and Hubbard, J. H.. On the dynamics of polynomial-like mappings. Ann. Sci. Éc. Norm. Sup. 4° série, t. 18 (1985), 287–343.CrossRefGoogle Scholar
[Do1]Douady, A.. Systémes dynamiques holomorphes, Séminaire Bourbaki No. 599 (1982). Asterique 105–106 (1983), 39–63.Google Scholar
[Do2]Douady, A.. Disques de Siegel et anneaux de Herman, Séminaire Bourbaki No. 677 (1986). Asterique 152–153 (1987), 151–172.Google Scholar
[Do3]Douady, A.. Algorithms for computing angles in the Mandelbrot set. Chaotic Dynamics and Fractals. Eds Barnsley, M. F. and Demko, S. G.. Academic Press, Atlanta, 1986, pp. 155–168.CrossRefGoogle Scholar
[Do4]Douady, A.. Descriptions of compact sets in ℂ. Topological Methods in Modern Mathematics. Publish or Perrish, Houston, 1993, pp. 429–465.Google Scholar
[Do5]Douady, A.. Does a Julia set depend continuously on the polynomial. Proc. Symposia in Applied Math., AMS. 49 (1994), 91–138.CrossRefGoogle Scholar
[GM]Goldberg, L. R. and Milnor, J.. Fixed points of polynomial maps II: fixed point portraits. Ann. Sci. Éc. Norm. Sup. 26 (1993), 51–98.CrossRefGoogle Scholar
[Fo]Forster, O.. Lectures on Riemann Surfaces. GTM 81. Springer, 1981.CrossRefGoogle Scholar
[HY]Hocking, J. G. and Young, G. S.. Topology. Dover, New York, 1988.Google Scholar
[Ji]Jiang, Y.. The renormalization method and quadratic-like maps. Preprint. MSRI No 081–95, Berkeley.Google Scholar
[La]Lavaurs, P.. These: Systémes dynamiques holomorphes: explosion de points périodiques paraboliques. Université de Paris-Sud Centre d'Orsay, 1989.Google Scholar
[Ly]Lyubich, M.. Geometry of quadratic polynomials: moduli, rigidity and local connectivity. Preprint. IMS at StonyBrook, 1993.Google Scholar
[Mi]Milnor, J.. Dynamics in one complex variable: introductory lectures. Preprint #1990//5. SUNY StonyBrook Institute for Mathematical Sciences, 1990.Google Scholar
[Pe1]Petersen, C. L.. On the Pommerenke-Levin-Yoccoz inequality. Ergod. Th. & Dynam. Sys. 13 (1993),785–806.Google Scholar
[Pe2]Petersen, C. L.. Local connectivity of some Julia sets containing a circle with an irrational rotation. Acta Math. (1996), to appear.Google Scholar
[PM1]Perez-Marco, R.. Topology of Julia sets and hedgehogs. Prépublications Mathematiques d'Orsay 94–48, 1994.Google Scholar
[PM2]Perez-Marco, R.. Hedgehog's dynamics 1. Preprint. UCLA (Los Angeles), 1996.Google Scholar
[Po]Pommerenke, Ch.. Boundary Behaviour of Conformal Maps. GMV 299. Springer, 1992.CrossRefGoogle Scholar
[Ru]Rudin, W.. Real and Complex Analysis. Third Edn.McGraw-Hill, New York, 1986.Google Scholar
[Sh]Shishikura, M.. The Hausdorff dimension of the boundary of the Mandelbrot set and Julia Set. Ann. Math. (1996), to appear.Google Scholar
[Sø]Sørensen, D. E. K.. Complex dynamical systems: rays and non-local connectivity. Ph.D. Thesis. MAT-DTU, 1994.Google Scholar