Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bula, Witold D.
and
Oversteegen, Lex G.
1990.
A characterization of smooth Cantor bouquets.
Proceedings of the American Mathematical Society,
Vol. 108,
Issue. 2,
p.
529.
Devaney, Robert L.
1993.
Knaster-like continua and complex dynamics.
Ergodic Theory and Dynamical Systems,
Vol. 13,
Issue. 4,
p.
627.
Rogers, James T.
1993.
Intrinsic rotations of simply connected regions and their boundaries.
Complex Variables, Theory and Application: An International Journal,
Vol. 23,
Issue. 1-2,
p.
17.
Bergweiler, Walter
1993.
Iteration of meromorphic functions.
Bulletin of the American Mathematical Society,
Vol. 29,
Issue. 2,
p.
151.
Aarts, Jan M.
and
Oversteegen, Lex G.
1993.
The geometry of Julia sets.
Transactions of the American Mathematical Society,
Vol. 338,
Issue. 2,
p.
897.
Devaney, Robert L.
2001.
Sex: Dynamics, topology, and bifurcations of complex exponentials.
Topology and its Applications,
Vol. 110,
Issue. 2,
p.
133.
Lee Deville, R.E.
2001.
Itineraries of entire functions.
Journal of Difference Equations and Applications,
Vol. 7,
Issue. 2,
p.
193.
Devaney, Robert
and
Jarque, Xavier
2002.
Indecomposable continua in exponential dynamics.
Conformal Geometry and Dynamics of the American Mathematical Society,
Vol. 6,
Issue. 1,
p.
1.
L.Devaney, Robert
2004.
Proceedings of the Sixth International Conference on Difference Equations Augsburg, Germany 2001.
p.
105.
DEVANEY, ROBERT L.
JARQUE, XAVIER
and
ROCHA, MÓNICA MORENO
2005.
INDECOMPOSABLE CONTINUA AND MISIUREWICZ POINTS IN EXPONENTIAL DYNAMICS.
International Journal of Bifurcation and Chaos,
Vol. 15,
Issue. 10,
p.
3281.
Barański, Krzysztof
2007.
Trees and hairs for some hyperbolic entire maps of finite order.
Mathematische Zeitschrift,
Vol. 257,
Issue. 1,
p.
33.
L. Devaney, Robert
2007.
Open Problems in Topology II.
p.
469.
Schleicher, Dierk
2010.
Holomorphic Dynamical Systems.
Vol. 1998,
Issue. ,
p.
295.
2010.
Vol. 3,
Issue. ,
p.
125.
Dijkstra, Jan J.
and
van Mill, Jan
2012.
Negligible sets in Erdős spaces.
Topology and its Applications,
Vol. 159,
Issue. 13,
p.
2947.
OSBORNE, JOHN
2013.
Connectedness properties of the set where the iterates of an entire function are bounded.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 155,
Issue. 3,
p.
391.
Bergweiler, Walter
and
Peter, Jörn
2013.
Escape rate and Hausdorff measure for entire functions.
Mathematische Zeitschrift,
Vol. 274,
Issue. 1-2,
p.
551.
Devaney, Robert L.
2014.
Fractals, Wavelets, and their Applications.
Vol. 92,
Issue. ,
p.
61.
Hittmeyer, Stefanie
Krauskopf, Bernd
and
Osinga, Hinke M.
2015.
Interactions of the Julia Set with Critical and (Un)Stable Sets in an Angle-Doubling Map on ℂ\{0}.
International Journal of Bifurcation and Chaos,
Vol. 25,
Issue. 04,
p.
1530013.
Devaney, Robert L.
2016.
Exotic topology in complex dynamics.
Indagationes Mathematicae,
Vol. 27,
Issue. 5,
p.
1116.

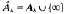 is a connected subspace of the Riemann sphere
is a connected subspace of the Riemann sphere 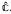 . As a corollary,
. As a corollary, 