Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
DÍAZ, LORENZO J.
and
GORODETSKI, ANTON
2009.
Non-hyperbolic ergodic measures for non-hyperbolic homoclinic classes.
Ergodic Theory and Dynamical Systems,
Vol. 29,
Issue. 5,
p.
1479.
Bonatti, Christian
Díaz, Lorenzo J
and
Gorodetski, Anton
2010.
Non-hyperbolic ergodic measures with large support.
Nonlinearity,
Vol. 23,
Issue. 3,
p.
687.
Lee, Manseob
2011.
Stably average shadowable homoclinic classes.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 74,
Issue. 2,
p.
689.
Fakhari, Abbas
2011.
C1-stably ℒpshadowable homoclinic classes.
Dynamical Systems,
Vol. 26,
Issue. 1,
p.
1.
Dai, XiongPing
2011.
Hyperbolicity of C 1-star invariant sets for C 1-class dynamical systems.
Science China Mathematics,
Vol. 54,
Issue. 2,
p.
269.
Lee, Manseob
and
Park, Junmi
2012.
ASYMPTOTIC AVERAGE SHADOWING PROPERTY ON A CLOSED SET.
Journal of the Chungcheong Mathematical Society,
Vol. 25,
Issue. 1,
p.
27.
DAI, Xiongping
2012.
Dominated splitting of differentiable dynamics with $\mathrm{C}^1$-topological weak-star property.
Journal of the Mathematical Society of Japan,
Vol. 64,
Issue. 4,
Lee, Keon-Hee
and
Wen, Xiao
2012.
SHADOWABLE CHAIN TRANSITIVE SETS OF C1-GENERIC DIFFEOMORPHISMS.
Bulletin of the Korean Mathematical Society,
Vol. 49,
Issue. 2,
p.
263.
Fakhari, Abbas
2012.
Periodically Expansive Homoclinic Classes.
Journal of Dynamics and Differential Equations,
Vol. 24,
Issue. 3,
p.
561.
Ahn, Jiweon
Lee, Keonhee
and
Lee, Manseob
2012.
Homoclinic classes with shadowing.
Journal of Inequalities and Applications,
Vol. 2012,
Issue. 1,
Bessa, Mário
Rocha, Jorge
and
Torres, Maria Joana
2013.
Shades of hyperbolicity for Hamiltonians.
Nonlinearity,
Vol. 26,
Issue. 10,
p.
2851.
Lee, Manseob
2013.
Chain components with C 1 -stably orbital shadowing.
Advances in Difference Equations,
Vol. 2013,
Issue. 1,
Das, Tarun
Lee, Keonhee
and
Lee, Manseob
2013.
C1-persistently continuum-wise expansive homoclinic classes and recurrent sets.
Topology and its Applications,
Vol. 160,
Issue. 2,
p.
350.
Lee, Manseob
and
Park, Junmi
2013.
ROBUSTLY CHAIN TRANSITIVE SETS WITH SHADOWING.
Journal of the Chungcheong Mathematical Society,
Vol. 26,
Issue. 4,
p.
821.
Sakai, Kazuhiro
2013.
Shadowable chain transitive sets.
Journal of Difference Equations and Applications,
Vol. 19,
Issue. 10,
p.
1601.
Bessa, Mario
2013.
C1-STABLY SHADOWABLE CONSERVATIVE DIFFEOMORPHISMS ARE ANOSOV.
Bulletin of the Korean Mathematical Society,
Vol. 50,
Issue. 5,
p.
1495.
Bessa, Mário
Lee, Manseob
and
Vaz, Sandra
2014.
Stable weakly shadowable volume-preserving systems are volume-hyperbolic.
Acta Mathematica Sinica, English Series,
Vol. 30,
Issue. 6,
p.
1007.
Lee, Manseob
and
Park, Junmi
2014.
Chain components with stably limit shadowing property are hyperbolic.
Advances in Difference Equations,
Vol. 2014,
Issue. 1,
Ahmadi, Seyyed Alireza
2014.
On the topology of the chain recurrent set of a dynamical system.
Applied General Topology,
Vol. 15,
Issue. 2,
p.
167.
Bessa, Mario
and
Vaz, Sandra
2014.
STABLE WEAK SHADOWABLE SYMPLECTOMORPHISMS ARE PARTIALLY HYPERBOLIC.
Communications of the Korean Mathematical Society,
Vol. 29,
Issue. 2,
p.
285.

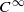 manifold
manifold 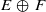 (where the dimension of
(where the dimension of 