Hostname: page-component-76c49bb84f-hwk5l Total loading time: 0 Render date: 2025-07-08T20:37:55.152Z Has data issue: false hasContentIssue false
  • English
  • Français

Certain properties for crossed products by automorphisms with a certain non-simple tracial Rokhlin property

Published online by Cambridge University Press:  03 September 2012

XIAOCHUN FANG  and
QINGZHAI FAN
XIAOCHUN FANG
Affiliation:
Department of Mathematics, Shanghai Maritime University, 1550 Haigang Ave, New Harbor City, Shanghai 201306, China (email: qzfan@shmtu.edu.cn) Department of Mathematics, Tongji University, Shanghai 200092, China (email: xfang@mail.tongji.edu.cn)
QINGZHAI FAN
Affiliation:
Department of Mathematics, Shanghai Maritime University, 1550 Haigang Ave, New Harbor City, Shanghai 201306, China (email: qzfan@shmtu.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 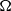$\Omega $ be a class of unital 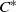$C^*$-algebras. Then any simple unital 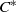$C^*$-algebra 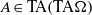$A\in \mathrm {TA}(\mathrm {TA}\Omega )$ is a 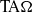$\mathrm {TA}\Omega $ algebra. Let 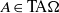$A\in \mathrm {TA}\Omega $ be an infinite-dimensional $\alpha $-simple unital 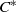$C^*$-algebra with the property SP. Suppose that 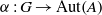$\alpha :G\to \mathrm {Aut}(A)$ is an action of a finite group 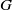$G$ on 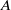$A$ which has a certain non-simple tracial Rokhlin property. Then the crossed product algebra 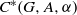$C^*(G,A,\alpha )$ belongs to 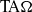$\mathrm {TA}\Omega $.

Information

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 5 , October 2013 , pp. 1391 - 1400
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

[1]Connes, A.. Outer conjugacy classes of automorphisms of factors. Ann. Sci. Éc. Norm. Supér. 8 (1975), 383–419.Google Scholar
[2]Elliott, G. A.. On the classification of the inductive limts of sequences of semisimple finite dimensional algebras. J. Algebra 38 (1976), 29–44.Google Scholar
[3]Elliott, G. A.. On the classification of $C^*$-algebras of real rank zero. J. Reine Angew. Math. 443 (1993), 179–219.Google Scholar
[4]Elliott, G. A. and Gong, G.. On the classification of $C^*$-algebras of real rank zero, II. Ann. of Math. (2) 144 (1996), 497–610.Google Scholar
[5]Elliott, G. A. and Niu, Z.. On tracial approximation. J. Funct. Anal. 254 (2008), 396–440.Google Scholar
[6]Fan, Q. and Fang, X.. Stable rank one and real rank zero for crossed products by automorphisms with the tracial Rokhlin property. Chin. Ann. Math. Ser. B 30 (2009), 179–186.Google Scholar
[7]Fan, Q.. Some $C^*$-algebras properties preserved by tracial approximation. Israel J. Math., to appear.Google Scholar
[8]Fan, Q. and Fang, X.. Non-simple tracial approximation. Houston J. Math. 37 (2011), 1249–1263.Google Scholar
[9]Fan, Q.. Classification of certain simple $C^*$-algebras. J. Ramanujan Math. Soc. 26 (2011), 1–7.Google Scholar
[10]Herman, R. and Ocneanu, A.. Stability for integer actions on UHF $C^*$-algebras. J. Funct. Anal. 59 (1984), 132–144.CrossRefGoogle Scholar
[11]Hua, J.. The tracial Rokhlin property for automorphisms of non-simple $C^*$-algebras. Chin. Ann. Math. Ser. B 31 (2010), 191–200.Google Scholar
[12]Kishimoto, A.. The Rohlin property for shifts on UHF algebras. J. Reine Angew. Math. 465 (1995), 183–196.Google Scholar
[13]Lin, H.. The tracial topological rank of $C^*$-algebras. Proc. Lond. Math. Soc. 83 (2001), 199–234.Google Scholar
[14]Lin, H.. An Introduction to the Classification of Amenable $C^*$-algebras. World Scientific, Singapore, 2001.Google Scholar
[15]Lin, H.. Classification of simple $C^*$-algebras with tracial topological rank zero. Duke. Math. J. 125 (2005), 91–119.Google Scholar
[16]Lin, H.. Classification of simple $C^*$-algebras with tracial rank one. J. Funct. Anal. 254 (2008), 396–440.Google Scholar
[17]Osaka, H. and Phillips, N. C.. Stable and real rank for crossed products by automorphisms with the tracial Rokhlin property. Ergod. Th. & Dynam. Sys. 26 (2006), 1579–1621.Google Scholar
[18]Phillips, N. C.. Crossed products by finite cyclic group actions with the tracial Rokhlin property, arXiv preprint math. OA/0306410.Google Scholar
[19]Phillips, N. C.. The tracial Rokhlin property for actions of finite groups on $C^*$-algebras, arXiv preprint math. OA/0609782.Google Scholar
[20]Rordam, M.. Classification of certain infinite simple $C^*$-algebras. J. Funct. Anal. 131 (1995), 415–458.Google Scholar
[21]Yang, X. and Fang, X.. The tracial rank for crossed products by finite group action. Rocky Mountain J. Math. 42 (2012), 339–352.Google Scholar