Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-05-16T17:20:23.327Z Has data issue: false hasContentIssue false
  • English
  • Français

A characterization of topologically completely positive entropy for shifts of finite type

Published online by Cambridge University Press:  03 June 2013

RONNIE PAVLOV
RONNIE PAVLOV*
Affiliation:
Department of Mathematics, University of Denver, 2360 S. Gaylord St., Denver, CO 80208, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

A topological dynamical system was defined by Blanchard [Fully Positive Topological Entropy and Topological Mixing (Symbolic Dynamics and Applications (in honor of R. L. Adler), 135). American Mathematical Society Contemporary Mathematics, Providence, RI, 1992, pp. 95–105] to have topologically completely positive entropy (or TCPE) if its only zero entropy factor is the dynamical system consisting of a single fixed point. For 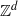${ \mathbb{Z} }^{d} $ shifts of finite type, we give a simple condition equivalent to having TCPE. We use our characterization to derive a similar equivalent condition to TCPE for the subclass of 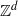${ \mathbb{Z} }^{d} $ group shifts, which was proved by Lind and Schmidt in the abelian case [Homoclinic points of algebraic 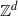${ \mathbb{Z} }^{d} $-actions. J. Amer. Math. Soc. 12(4) (1999), 953–980] and by Boyle and Schraudner in the general case [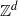${ \mathbb{Z} }^{d} $ group shifts and Bernoulli factors. Ergod. Th. & Dynam. Sys. 28(2) (2008), 367–387]. We also give an example of a 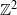${ \mathbb{Z} }^{2} $ shift of finite type which has TCPE but is not even topologically transitive, and prove a result about block gluing 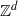${ \mathbb{Z} }^{d} $ SFTs motivated by our characterization of TCPE.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 6 , December 2014 , pp. 2054 - 2065
Copyright
© Cambridge University Press, 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blanchard, F.. Fully Positive Topological Entropy and Topological Mixing (Symbolic Dynamics and Applications (in Honor of R. L. Adler), 135). American Mathematical Society Contemporary Mathematics, Providence, RI, 1992, pp. 95–105.Google Scholar
Boyle, M., Pavlov, R. and Schraudner, M.. Multidimensional sofic shifts without separation, and their factors. Trans. Amer. Math. Soc. 362 (2010), 4617–4653.Google Scholar
Boyle, M. and Schraudner, M.. ${ \mathbb{Z} }^{d} $ group shifts and Bernoulli factors. Ergod. Th. & Dynam. Sys. 28 (2) (2008), 367–387.Google Scholar
Kitchens, B. and Schmidt, K.. Automorphisms of compact groups. Ergod. Th. & Dynam. Sys. 9 (4) (1989), 691–735.Google Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.Google Scholar
Lind, D. and Schmidt, K.. Homoclinic points of algebraic ${ \mathbb{Z} }^{d} $-actions. J. Amer. Math. Soc. 12 (4) (1999), 953–980.Google Scholar
Petersen, K. and Schmidt, K.. Symmetric Gibbs measures. Trans. Amer. Math. Soc. 349 (7) (1997), 2775–2811.Google Scholar
Quas, A. and Sahin, A.. Entropy gaps and locally maximal entropy in ${ \mathbb{Z} }^{d} $ subshifts. Ergod. Th. & Dynam. Sys. 23 (2003), 1227–1245.Google Scholar