Article contents
Classification and rigidity of totally periodic pseudo-Anosov flows in graph manifolds
Published online by Cambridge University Press: 03 July 2014
Abstract
In this article we analyze totally periodic pseudo-Anosov flows in graph 3-manifolds. This means that in each Seifert fibered piece of the torus decomposition, the free homotopy class of regular fibers has a finite power which is also a finite power of the free homotopy class of a closed orbit of the flow. We show that each such flow is topologically equivalent to one of the model pseudo-Anosov flows which we previously constructed in Barbot and Fenley (Pseudo-Anosov flows in toroidal manifolds. Geom. Topol. 17 (2013), 1877–1954). A model pseudo-Anosov flow is obtained by glueing standard neighborhoods of Birkhoff annuli and perhaps doing Dehn surgery on certain orbits. We also show that two model flows on the same graph manifold are isotopically equivalent (i.e. there is a isotopy of 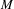 $M$ mapping the oriented orbits of the first flow to the oriented orbits of the second flow) if and only if they have the same topological and dynamical data in the collection of standard neighborhoods of the Birkhoff annuli.
$M$ mapping the oriented orbits of the first flow to the oriented orbits of the second flow) if and only if they have the same topological and dynamical data in the collection of standard neighborhoods of the Birkhoff annuli.
Information
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2014
References
- 11
- Cited by

