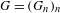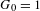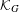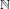Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Iacò, Maria Rita
Steiner, Wolfgang
and
Tichy, Robert F.
2016.
Linear Recursive Odometers and Beta-Expansions.
Uniform distribution theory,
Vol. 11,
Issue. 1,
p.
175.
Berthé, Valérie
Frougny, Christiane
Rigo, Michel
and
Sakarovitch, Jacques
2020.
The carry propagation of the successor function.
Advances in Applied Mathematics,
Vol. 120,
Issue. ,
p.
102062.
Madritsch, Manfred G.
and
Thuswaldner, Jörg M.
2022.
The level of distribution of the sum-of-digits function of linear recurrence number systems.
Journal de théorie des nombres de Bordeaux,
Vol. 34,
Issue. 2,
p.
449.