Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-29T18:05:36.968Z Has data issue: false hasContentIssue false
  • English
  • Français

Compensation functions for factors of shifts of finite type

Published online by Cambridge University Press:  02 October 2014

JOHN ANTONIOLI Open the ORCID record for JOHN ANTONIOLI [Opens in a new window]
JOHN ANTONIOLI*
Affiliation:
Department of Mathematics and Statistics, University of Victoria, 3800 Finnerty Road, Victoria, BC, Canada  V8W 3R4 email antoniol@uvic.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 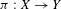${\it\pi}:X\rightarrow Y$ be an infinite-to-one factor map, where $X$ is a shift of finite type. A compensation function relates equilibrium states on 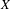$X$ to equilibrium states on $Y$. The 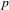$p$-Dini condition is given as a way of measuring the smoothness of a continuous function, with $1$-Dini corresponding to functions with summable variation. Two types of compensation functions are defined in terms of this condition. 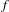Given a fully supported invariant measure ${\it\nu}$ on $Y$, we show that the relative equilibrium states of a $1$-Dini function $f$ over ${\it\nu}$ are themselves fully supported, and have positive relative entropy. We then show that there exists a compensation function which is 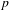$p$-Dini for all $p>1$ which has relative equilibrium states supported by a subshift on which ${\it\pi}$ is a finite-to-one map onto $Y$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 2 , April 2016 , pp. 375 - 389
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allahbakhshi, M. and Quas, A.. Class degree and relative maximal entropy. Trans. Amer. Math. Soc. 365(3) (2013), 1347–1368.CrossRefGoogle Scholar
Boyle, M. and Petersen, K.. Hidden Markov processes in the context of symbolic dynamics. Entropy of Hidden Markov Processes and Connections to Dynamical Systems (London Mathematical Society Lecture Note Series, 385). Cambridge University Press, Cambridge, 2011, pp. 5–71.CrossRefGoogle Scholar
Boyle, M. and Tuncel, S.. Infinite-to-one codes and Markov measures. Trans. Amer. Math. Soc. 285(2) (1984), 657–684.CrossRefGoogle Scholar
Góra, P. and Schmitt, B.. Un exemple de transformation dilatante et C 1 par morceaux de l’intervalle, sans probabilité absolument continue invariante. Ergod. Th. & Dynam. Sys. 9(1) (1989), 101–113.CrossRefGoogle Scholar
Hofbauer, F.. Examples for the nonuniqueness of the equilibrium state. Trans. Amer. Math. Soc. 228 (1977), 223–241.CrossRefGoogle Scholar
Keller, G.. Equilibrium States in Ergodic Theory (London Mathematical Society Student Texts, 42). Cambridge University Press, Cambridge, 1998.CrossRefGoogle Scholar
Ledrappier, F. and Walters, P.. A relativised variational principle for continuous transformations. J. Lond. Math. Soc. (2) 16(3) (1977), 568–576.CrossRefGoogle Scholar
Marcus, B., Petersen, K. and Williams, S.. Transmission rates and factors of Markov chains. Conference in Modern Analysis and Probability (New Haven, CT, 1982) (Contemporary Mathematics, 26). American Mathematical Society, Providence, RI, 1984, pp. 279–293.CrossRefGoogle Scholar
Petersen, K.. Ergodic Theory (Cambridge Studies in Advanced Mathematics, 2). Cambridge University Press, Cambridge, 1989.Google Scholar
Petersen, K., Quas, A. and Shin, S.. Measures of maximal relative entropy. Ergod. Th. & Dynam. Sys. 23(1) (2003), 207–223.CrossRefGoogle Scholar
Petersen, K. and Shin, S.. On the definition of relative pressure for factor maps on shifts of finite type. Bull. Lond. Math. Soc. 37(4) (2005), 601–612.CrossRefGoogle Scholar
Rudolph, D. J.. Ergodic theory on Lebesgue spaces. Fundamentals of Measurable Dynamics (Oxford Science Publications). The Clarendon Press, Oxford University Press, New York, 1990.Google Scholar
Shin, S.. Measures that maximize weighted entropy for factor maps between subshifts of finite type. Ergod. Th. & Dynam. Sys. 21(4) (2001), 1249–1272.CrossRefGoogle Scholar
Walters, P.. Ruelle’s operator theorem and g-measures. Trans. Amer. Math. Soc. 214 (1975), 375–387.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer, New York, 1982.CrossRefGoogle Scholar
Walters, P.. Relative pressure, relative equilibrium states, compensation functions and many-to-one codes between subshifts. Trans. Amer. Math. Soc. 296(1) (1986), 1–31.CrossRefGoogle Scholar
Yayama, Y.. Existence of a measurable saturated compensation function between subshifts and its applications. Ergod. Th. & Dynam. Sys. 31(5) (2011), 1563–1589.CrossRefGoogle Scholar
Yoo, J.. Measures of maximal relative entropy with full support. Ergod. Th. & Dynam. Sys. 31(6) (2011), 1889–1899.CrossRefGoogle Scholar