Hostname: page-component-76c49bb84f-lvrpm Total loading time: 0 Render date: 2025-07-08T14:49:52.815Z Has data issue: false hasContentIssue false
  • English
  • Français

Continued fraction algorithm for Sturmian colorings of trees

Published online by Cambridge University Press:  12 December 2017

DONG HAN KIM  and
SEONHEE LIM
DONG HAN KIM
Affiliation:
Department of Mathematics Education, Dongguk University–Seoul, 30 Pildong-ro 1-gil, Jung-gu, Seoul 04620, Republic of Korea email kim2010@dongguk.edu
SEONHEE LIM
Affiliation:
Department of Mathematics Education, Dongguk University–Seoul, 30 Pildong-ro 1-gil, Jung-gu, Seoul 04620, Republic of Korea email kim2010@dongguk.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Factor complexity 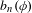$b_{n}(\unicode[STIX]{x1D719})$ for a vertex coloring 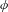$\unicode[STIX]{x1D719}$ of a regular tree is the number of classes of $n$-balls up to color-preserving automorphisms. Sturmian colorings are colorings of minimal unbounded factor complexity 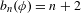$b_{n}(\unicode[STIX]{x1D719})=n+2$. In this article, we prove an induction algorithm for Sturmian colorings using colored balls in a way analogous to the continued fraction algorithm for Sturmian words. Furthermore, we characterize Sturmian colorings in terms of the data appearing in the induction algorithm.

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 9 , September 2019 , pp. 2541 - 2569
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Arnoux, P. and Rauzy, G.. Représentation géométrique des suites de complexité 2n + 1. Bull. Soc. Math. France 119 (1991), 199–215.Google Scholar
Avni, N., Lim, S. and Nevo, E.. On commensurator growth. Israel J. Math. 188 (2012), 259–279.Google Scholar
Bass, H. and Lubotzky, A.. Tree Lattices (Progress in Mathematics, 176) . Birkhauser, Boston, 2000.Google Scholar
Burger, M. and Mozes, S.. CAT (-1)-spaces, divergence groups and their commensurators. J. Amer. Math. Soc. 9 (1996), 57–93.Google Scholar
Cassaigne, J.. On a conjecture of J. Shallit. Automata, Languages and Programming (Bologna, 1997) (Lecture Notes in Computer Science, 1256) . Springer, Berlin, 1997, pp. 693–704.Google Scholar
Hedlund, G. A. and Morse, M.. Symbolic dynamics II: Sturmian trajectories. Amer. J. Math. 62 (1940), 1–42.Google Scholar
Kim, D. H. and Lim, S.. Hyperbolic tessellation and colorings of trees. Abstr. Appl. Anal. 2013 (2013), ID 706496.Google Scholar
Kim, D. H. and Lim, S.. Subword complexity and Sturmian colorings of regular trees. Ergod. Th. & Dynam. Sys. 35(2) (2015), 461–481.Google Scholar
Lothaire, M.. Algebraic Combinatorics on Words (Encyclopedia of Mathematics and its Applications, 90) . Cambridge University Press, Cambridge, 2002.Google Scholar
Lubotzky, A., Mozes, S. and Zimmer, R.. Superrigidity for the commensurability group of tree lattices. Comment. Math. Helv. 69(4) (1994), 523–548.Google Scholar
Pytheas Fogg, N.. Substitutions in Dynamics, Arithmetics and Combinatorics (Lecture Notes in Mathematics, 1794) . Eds. Berth, V., Ferenczi, S., Mauduit, C. and Siegel, A.. Springer, Berlin, 2002.Google Scholar
Rauzy, G.. Suite à termes dans un alphabet fini. Sém. Théor. Nombres Bordeaux 25 (1982–1983), 1–16.Google Scholar
Rauzy, G.. Mots infinis en arithmétiques. Automata on Infinite Words (Lecture Notes in Computer Science, 192) . Eds. Nivat, M. and Perrin, D.. Springer, Berlin, 1985, pp. 165–171.Google Scholar
Serre, J.-P.. Trees. Springer, Berlin, 1980. Translated from the French by John Stillwell.Google Scholar