Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rosenblatt, Joseph
1991.
Almost Everywhere Convergence II.
p.
227.
Rosenblatt, Joseph M.
and
Wierdl, Mate
1992.
A new maximal inequality and its applications.
Ergodic Theory and Dynamical Systems,
Vol. 12,
Issue. 3,
p.
509.
Jones, Roger L.
and
Olsen, James
1992.
Subsequence pointwise ergodic theorems for operators inL p.
Israel Journal of Mathematics,
Vol. 77,
Issue. 1-2,
p.
33.
Bellow, Alexandra
Jones, Roger L.
and
Rosenblatt, Joseph
1992.
Almost everywhere convergence of weighted averages.
Mathematische Annalen,
Vol. 293,
Issue. 1,
p.
399.
Jones, Roger L.
and
Wierdl, Mate
1994.
Convergence and divergence of ergodic averages.
Ergodic Theory and Dynamical Systems,
Vol. 14,
Issue. 3,
p.
515.
Bellow, Alexandra
Jones, Roger
and
Rosenblatt, Joseph
1994.
Almost everywhere convergence of convolution powers.
Ergodic Theory and Dynamical Systems,
Vol. 14,
Issue. 3,
p.
415.
Reinhold-Larsson, Karin
1994.
Discrepancy of behavior of perturbed sequences in 𝐿^{𝑝} spaces.
Proceedings of the American Mathematical Society,
Vol. 120,
Issue. 3,
p.
865.
McIntosh, David I.
1995.
Ergodic Averages for Weight Functions Moved by Non-Linear Transformations on ℝn.
Canadian Journal of Mathematics,
Vol. 47,
Issue. 4,
p.
852.
Ferrando, S. E.
1995.
Moving Ergodic Theorems for Superadditive Processes.
Canadian Journal of Mathematics,
Vol. 47,
Issue. 4,
p.
728.
Akcoglu, Mustafa
Bellow, Alexandra
Jones, Roger L.
Losert, Viktor
Reinhold-Larsson, Karin
and
Wierdl, Máté
1996.
The strong sweeping out property for lacunary sequences, Riemann sums, convolution powers, and related matters.
Ergodic Theory and Dynamical Systems,
Vol. 16,
Issue. 2,
p.
207.
Jones, Roger L.
and
Wierdl, Μáté
1996.
Convergence in Ergodic Theory and Probability.
p.
229.
Çömez, Doğan
1998.
Moving Averages of Superadditive Processes with Respect to $L_p$-Contractions, $1\lt p\lt \infty$.
Rocky Mountain Journal of Mathematics,
Vol. 28,
Issue. 3,
Çömez, Doğan
and
Litvinov, Semyon
2000.
Norm Convergence of Moving Averages for $\tau$-Integrable Operators.
Rocky Mountain Journal of Mathematics,
Vol. 30,
Issue. 4,
Gamet, C.
and
Weber, M.
2000.
Entropy Numbers of Some Ergodic Averages.
Theory of Probability & Its Applications,
Vol. 44,
Issue. 4,
p.
650.
Lifshits, Mikhail
and
Weber, Michel
2003.
Régularisation spectrale et propriétés métriques des moyennes mobiles.
Journal d'Analyse Mathématique,
Vol. 89,
Issue. 1,
p.
1.
del Junco, Andrés
2009.
Ergodic Theory.
p.
79.
Junco, Andrés del
2009.
Encyclopedia of Complexity and Systems Science.
p.
2933.
Havard, François
and
Lesigne, Emmanuel
2010.
Averages on annuli of Euclidean space.
Advances in Pure and Applied Mathematics,
Vol. 1,
Issue. 2,
Moonens, Laurent
and
Rosenblatt, Joseph M.
2012.
Moving averages in the plane.
Illinois Journal of Mathematics,
Vol. 56,
Issue. 3,
Komech, S. A.
2012.
Boundary distortion rate in synchronized systems: Geometrical meaning of entropy.
Problems of Information Transmission,
Vol. 48,
Issue. 1,
p.
11.

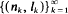 be a sequence of pairs of positive integers, and define the sequence of averaging operators
be a sequence of pairs of positive integers, and define the sequence of averaging operators 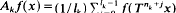 . Necessary and sufficient conditions are given forthis sequence of averages to converge almost everywhere. Weighted versions are also considered.
. Necessary and sufficient conditions are given forthis sequence of averages to converge almost everywhere. Weighted versions are also considered.