Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-19T23:34:25.063Z Has data issue: false hasContentIssue false
  • English
  • Français

Diffeomorphism group valued cocycles over higher-rank abelian Anosov actions

Published online by Cambridge University Press:  05 April 2018

DANIJELA DAMJANOVIĆ  and
DISHENG XU
DANIJELA DAMJANOVIĆ
Affiliation:
Department of Mathematics, Kungliga Tekniska Högskolan, Lindstedtsvägen 25, SE-100 44 Stockholm, Sweden email ddam@kth.se, dishengxu1989@gmail.com
DISHENG XU
Affiliation:
Department of Mathematics, Kungliga Tekniska Högskolan, Lindstedtsvägen 25, SE-100 44 Stockholm, Sweden email ddam@kth.se, dishengxu1989@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that every smooth diffeomorphism group valued cocycle over certain 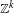$\mathbb{Z}^{k}$ Anosov actions on tori (and more generally on infranilmanifolds) is a smooth coboundary on a finite cover, if the cocycle is center bunched and trivial at a fixed point. For smooth cocycles which are not trivial at a fixed point, we have smooth reduction of cocycles to constant ones, when lifted to the universal cover. These results on cocycle trivialization apply, via the existing global rigidity results, to maximal Cartan 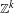$\mathbb{Z}^{k}$ (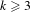$k\geq 3$) actions by Anosov diffeomorphisms (with at least one transitive), on any compact smooth manifold. This is the first rigidity result for cocycles over 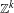$\mathbb{Z}^{k}$ actions with values in diffeomorphism groups which does not require any restrictions on the smallness of the cocycle or on the diffeomorphism group.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 1 , January 2020 , pp. 117 - 141
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, A., Kocsard, A. and Liu, X.. Livsic theorem for diffeomorphism cocycles. In preparation. Preprint, 2017, https://arxiv.org/abs/1711.02135.Google Scholar
Bercovici, H. and Niţic̆, V.. Cohomology of higher rank abelian Anosov actions for Banach algebra valued cocycles. AIMS Conference Publications 2001 (Special) (2001), 50–55.Google Scholar
Burns, K. and Wilkinson, A.. On the ergodicity of partially hyperbolic systems. Ann. of Math. (2) 171 (2010), 451–489.Google Scholar
Butler, C. and Xu, D.. Uniformly quasiconformal partially hyperbolic systems. Ann. Sci. Éc. Norm. Supér, Preprint, 2016, arXiv:1601.07485, to appear.Google Scholar
Crovisier, S. and Potrie, R.. Introduction to partially hyperbolic dynamics. School on Dynamical Systems, ICTP, Trieste, 2015.Google Scholar
Damjanovic, D. and Katok, A.. Periodic cycle functions and cocycle rigidity for certain partially hyperbolic ℝ k actions. Discrete Contin. Dyn. Syst. 13(4) (2005), 985–1005.Google Scholar
Damjanović, D. and Xu, D.. On conservative partially hyperbolic actions with compact center foliation. Preprint, 2017, https://arxiv.org/pdf/1706.03626.pdf.Google Scholar
Franks, J.. Anosov diffeomorphisms on tori. Trans. Amer. Math. Soc. 145 (1969), 117–124.10.1090/S0002-9947-1969-0253352-7Google Scholar
Goetze, E. R. and Spatzier, R. J.. Smooth classification of Cartan actions of higher rank semisimple Lie groups and their lattices. Ann. of Math. (2) 150(3) (1999), 743–773.10.2307/121055Google Scholar
Hector, G. and Hirsch, U.. Introduction to the Geometry of Foliations. Part A, Vol. 1 (Aspects of Mathematics) . Vieweg & Teubner, Wiesdbaden, 1981.10.1007/978-3-322-98482-1Google Scholar
Hirsch, M., Pugh, C. and Shub, M.. Invariant Manifolds. Springer, New York, 1977.10.1007/BFb0092042Google Scholar
Journé, J.-L.. A regularity lemma for functions of several variables. Rev. Mat. Iberoam. 4(2) (1988), 187–193.10.4171/RMI/69Google Scholar
Katok, A. and Lewis, J.. Local rigidity for certain groups of toral automorphisms. Israel J. Math. 75(2) (1991), 203–241.10.1007/BF02776025Google Scholar
Katok, A. and Nitica, V.. Rigidity of higher rank abelian cocycles with values in diffeomorphism groups. Geom. Dedicata 124 (2007), 109–131.10.1007/s10711-006-9116-6Google Scholar
Katok, A. and Nitica, V.. Rigidity in Higher Rank Abelian Group Actions, Volume I, Introduction and Cocycle Problems. Cambridge University Press, Cambridge, 2011.10.1017/CBO9780511803550Google Scholar
Katok, A., Nitica, V. and Torok, A.. Nonabelian cohomology of abelian Anosov actions. Ergod. Th. & Dynam. Syst. 20 (2000), 259–288.Google Scholar
Katok, A. and Spatzier, R.. First cohomology of Anosov actions of higher rank abelian groups and applications to rigidity. Publ. Math. Inst. Hautes Études Sci. 79 (1994), 131–156.10.1007/BF02698888Google Scholar
Kalinin, B.. Livsic theorem for matrix cocycles. Ann. of Math. (2) 173 (2011), 1025–1042.10.4007/annals.2011.173.2.11Google Scholar
Kalinin, B. and Sadovskaya, V.. Global rigidity for totally non-symplectic Anosov ℤ k action. Geom. Topol. 10 (2006), 929–954.10.2140/gt.2006.10.929Google Scholar
Kalinin, B. and Sadovskaya, V.. On the classification of resonance free Anosov ℤ k action. Michigan Math. J. 55 (2007), 651–670.10.1307/mmj/1197056461Google Scholar
Kalinin, B. and Spatzier, R.. On the classification of Cartan actions. Geom. Funct. Anal. 17(2) (2007), 468–490.10.1007/s00039-007-0602-2Google Scholar
Kocsard, A. and Potrie, R.. Livsic theorem for low-dimensional diffeomorphism cocycles. Comment. Math. Helv. 91 (2016), 39–64.Google Scholar
Livsic, A. N.. Certain properties of the homology of Y-systems. Mat. Zametki 10 (1971), 555–564.Google Scholar
Livsic, A. N.. Cohomology of dynamical systems. Math. USSR Izv. 6 (1972), 1278–1301.10.1070/IM1972v006n06ABEH001919Google Scholar
de la Llave, R.. Smooth conjugacy and SRB measures for uniformly and non-uniformly hyperbolic systems. Commun. Math. Phys. 150(2) (1992), 289–320.10.1007/BF02096662Google Scholar
de la Llave, R. and Windsor, A.. Smooth dependence on parameters of solutions to cohomology equations over Anosov systems with applications to cohomology equations on diffeomorphism groups. Discrete Contin. Dynam. Syst. A 29 (2011), 1141–1154.Google Scholar
Mal’cev, A. I.. Nilpotent torsion-free groups. Izv. Akad. Nauk SSSR Ser. Mat. 13 (1949), 201–212 (in Russian).Google Scholar
Manning, A.. Anosov diffeomorphisms on nilmanifolds. Proc. Amer. Math. Soc. 38(2) (1973), 423–426.10.1090/S0002-9939-1973-0343317-5Google Scholar
Manning, A.. There are no new Anosov diffeomorphisms on tori. Amer. J. Math. 96(3) (1974), 422–429.Google Scholar
Nitica, V. and Torok, A.. Cohomology of dynamical systems and rigidity of partially hyperbolic actions of higher-rank lattices. Duke Math. J. 79(3) (1995), 751–810.10.1215/S0012-7094-95-07920-4Google Scholar
Nitica, V. and Torok, A.. Regularity of the transfer map for cohomologous cocycles. Ergod. Th. & Dynam. Syst. 18 (1998), 1187–1209.10.1017/S0143385798117480Google Scholar
Nitica, V. and Torok, A.. Local rigidity of certain partially hyperbolic actions of product type. Ergod. Th. & Dynam. Syst. 21 (2001), 1213–1237.10.1017/S0143385701001560Google Scholar
Nitica, V. and Torok, A.. Cocycles over abelian TNS actions. Geom. Dedicata 102(1) (2003), 65–90.10.1023/B:GEOM.0000006583.67322.55Google Scholar
Oseledec, V. I.. A multiplicative ergodic theorem. Lyapunov characteristic numbers for dynamical systems. Trans. Moscow Math. Soc 19(2) (1968), 197–231.Google Scholar
Pugh, C., Shub, M. and Wilkinson, A.. Hölder foliations. Duke Math. J. 86(3) (1997), 517–546.10.1215/S0012-7094-97-08616-6Google Scholar
Rodriguez Hertz, F. and Wang, Z.. Global rigidity of higher rank abelian Anosov algebraic actions. Invent. Math. 198(1) (2014), 165–209.10.1007/s00222-014-0499-yGoogle Scholar
Sadovskaya, V.. On uniformly quasiconformal Anosov systems. Math. Res. Lett. 12(2–3) (2005), 425–441.Google Scholar
Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc. 73 (1967), 747–817.10.1090/S0002-9904-1967-11798-1Google Scholar
Sondow, J. D.. Fixed points of Anosov maps of certain manifolds. Proc. Amer. Math. Soc. 61(2) (1976), 381–384.Google Scholar
Walters, P.. Conjugacy properties of affine transformations of nilmanifolds. Math. Syst. Theory 4(4) (1970), 327–333.Google Scholar