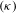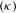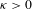Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kohlenbach, U.
and
Nicolae, A.
2017.
A Proof-Theoretic Bound Extraction Theorem for CAT $$(\kappa )$$ ( κ ) -Spaces.
Studia Logica,
Vol. 105,
Issue. 3,
p.
611.
Ferreira, Fernando
Leuştean, Laurenţiu
and
Pinto, Pedro
2019.
On the removal of weak compactness arguments in proof mining.
Advances in Mathematics,
Vol. 354,
Issue. ,
p.
106728.
Leuştean, Laurenţiu
and
Pinto, Pedro
2021.
Quantitative results on a Halpern-type proximal point algorithm.
Computational Optimization and Applications,
Vol. 79,
Issue. 1,
p.
101.
Kohlenbach, Ulrich
and
Sipoş, Andrei
2021.
The finitary content of sunny nonexpansive retractions.
Communications in Contemporary Mathematics,
Vol. 23,
Issue. 01,
p.
1950093.
Amini, Fardin
and
Saeidi, Shahram
2023.
Concepts of almost periodicity and ergodic theorems in locally convex spaces.
Journal of Fixed Point Theory and Applications,
Vol. 25,
Issue. 3,