Hostname: page-component-89b8bd64d-nlwjb Total loading time: 0 Render date: 2026-05-08T14:54:03.778Z Has data issue: false hasContentIssue false
  • English
  • Français

Equidistribution results for geodesic flows

Published online by Cambridge University Press:  04 January 2013

ABDELHAMID AMROUN
ABDELHAMID AMROUN*
Affiliation:
Département de Mathématiques, Université Paris Sud, CNRS UMR 8628, 91405 Orsay Cedex, France (email: Abdelhamid.Amroun@math.u-psud.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

Using the works of Mañé [On the topological entropy of the geodesic flows. J. Differential Geom.45 (1989), 74–93] and Paternain [Topological pressure for geodesic flows. Ann. Sci. Éc. Norm. Supér. (4) 33 (2000), 121–138] we study the distribution of geodesic arcs with respect to equilibrium states of the geodesic flow on a closed manifold, equipped with a 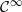$\mathcal {C}^{\infty }$Riemannian metric. We prove large-deviation lower and upper bounds and a contraction principle for the geodesic flow in the space of probability measures of the unit tangent bundle. We deduce a way of approximating equilibrium states for continuous potentials.

Information

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 3 , June 2014 , pp. 742 - 764
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

[1]Berger, M. and Bott, R.. Sur les variétés à courbure strictement positive. Topology 1 (1962).Google Scholar
[2]Burns, K. and Gutkin, E.. Growth of the number of geodesics between points and insecurity for Riemannian manifolds. Discrete Contin. Dyn. Syst. 21(2) (2008).Google Scholar
[3]Chengbo, Y.. Rigidity and dynamics around manifolds of negative curvature. Math. Res. Lett. 1 (1994), 123–147.Google Scholar
[4]Chengbo, Y.. The ergodic theory of discrete isometry groups on manifolds of variable negative curvature. Trans. Amer. Math. Soc. 348(12) (1996), 4965–5005.Google Scholar
[5]Dembo, A. and Zeitouni, O.. Large Deviations Techniques and Applications (Applications of Mathematics, 38). Springer, New York, 1998.Google Scholar
[6]Giles, J. R.. Convex Analysis with Application in Differentiation of Convex Functions (Research Notes in Mathematics, 58). Pitman, Boston, 1982.Google Scholar
[7]Keller, G.. Equilibrium States in Ergodic Theory (London Mathematical Society Study Texts, 42). Cambridge University Press, Cambridge, 1998.Google Scholar
[8]Kifer, Y.. Large deviations in dynamical systems and stochastic processes. Trans. Amer. Math. Soc. 321 (1988), 505–525.CrossRefGoogle Scholar
[9]Knieper, G.. The uniqueness of the measure of maximal entropy for geodesic flow on rank one manifolds. Ann. of Math. (2) 148 (1998), 291–314.Google Scholar
[10]Mañé, R.. On the topological entropy of the geodesic flows. J. Differential Geom. 45 (1989), 74–93.Google Scholar
[11]Newhouse, S.. Continuity properties of entropy. Ann. of Math. (2) 129 (1989), 215–235.Google Scholar
[12]Paternain, G. P.. Topological pressure for geodesic flows. Ann. Sci. Éc. Norm. Supér. (4) 33 (2000), 121–138.Google Scholar
[13]Paternain, G. P.. Geodesic Flows (Progress in Mathematics, 180). Birkhäuser, Basel, 2000.Google Scholar
[14]Rockafellar, R. T.. Convex Analysis. Princeton University Press, Princeton, NJ, 1970.Google Scholar
[15]Ruelle, D.. Thermodynamical Formalism (Encyclopedia of Mathematics and its Applications, 5). Addison-Wesley, Reading, MA, 1978.Google Scholar
[16]Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer, Berlin, 1982.Google Scholar