Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-06-08T03:08:06.065Z Has data issue: false hasContentIssue false
  • English
  • Français

Ergodic optimization in dynamical systems

Published online by Cambridge University Press:  24 January 2018

OLIVER JENKINSON
OLIVER JENKINSON*
Affiliation:
School of Mathematical Sciences, Queen Mary University of London, Mile End Road, London E1 4NS, UK email o.jenkinson@qmul.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

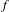Ergodic optimization is the study of problems relating to maximizing orbits and invariant measures, and maximum ergodic averages. An orbit of a dynamical system is called $f$-maximizing if the time average of the real-valued function 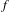$f$ along the orbit is larger than along all other orbits, and an invariant probability measure is called 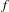$f$-maximizing if it gives 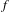$f$ a larger space average than any other invariant probability measure. In this paper, we consider the main strands of ergodic optimization, beginning with an influential model problem, and the interpretation of ergodic optimization as the zero temperature limit of thermodynamic formalism. We describe typical properties of maximizing measures for various spaces of functions, the key tool of adding a coboundary so as to reveal properties of these measures, as well as certain classes of functions where the maximizing measure is known to be Sturmian.

Type
Survey Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 10 , October 2019 , pp. 2593 - 2618
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Cambridge University Press, 2018

References

Addas-Zanata, S. and Tal, F. A.. Support of maximizing measures for typical C 0 dynamics on compact manifolds. Discrete Contin. Dyn. Syst. 26 (2010), 795–804.Google Scholar
Anagnostopoulou, V.. Sturmian measures and stochastic dominance in ergodic optimization. PhD Thesis, Queen Mary University of London, 2008.Google Scholar
Anagnostopoulou, V.. Stochastic dominance for shift-invariant measures. Discrete Contin. Dyn. Syst., to appear.Google Scholar
Anagnostopoulou, V., Díaz-Ordaz Avila, K., Jenkinson, O. and Richard, C.. Sturmian maximizing measures for the piecewise-linear cosine family. Bull. Braz. Math. Soc. (N.S.) 43 (2012), 285–302.Google Scholar
Anagnostopoulou, V. and Jenkinson, O.. Which beta-shifts have a largest invariant measure? J. Lond. Math. Soc. 72 (2009), 445–464.Google Scholar
Anantharaman, N.. On the zero-temperature or vanishing viscosity limit for Markov processes arising from Lagrangian dynamics. J. Eur. Math. Soc. (JEMS) 6 (2004), 207–276.Google Scholar
Aubrun, N. and Sablik, M.. Simulation of effective subshifts by two-dimensional subshifts of finite type. Acta Appl. Math. 126 (2013), 35–63.Google Scholar
Avramidou, P.. Optimization of ergodic averages along squares. Dyn. Syst. 25 (2010), 547–553.Google Scholar
Baladi, V.. Positive Transfer Operators and Decay of Correlations (Advanced Series in Nonlinear Dynamics, 16) . World Scientific, Singapore, 2000.Google Scholar
Baraviera, A., Cioletti, L., Lopes, A. O., Mohr, J. and Souza, R.. On the general one-dimensional XY model: positive and zero temperature, selection and non-selection. Rev. Math. Phys. 23 (2011), 1063–1113.Google Scholar
Baraviera, A. T., Leplaideur, R. and Lopes, A. O.. Selection of ground states in the zero temperature limit for a one-parameter family of potentials. SIAM J. Appl. Dyn. Syst. 11 (2012), 243–260.Google Scholar
Baraviera, A. T., Leplaideur, R. and Lopes, A. O.. Ergodic Optimization, Zero Temperature Limits and the Max-Plus Algebra, Publicações Matemáticas do IMPA (29 o Coloquio Brasileiro de Matemática) . IMPA, Rio de Janeiro, 2013.Google Scholar
Baraviera, A. T., Lopes, A. O. and Mengue, J.. On the selection of sub-action and measure for a subclass of potentials defined by P. Walters. Ergod. Th. & Dynam. Sys. 33 (2013), 1338–1362.Google Scholar
Baraviera, A. T., Lopes, A. O. and Thieullen, Ph.. A large deviation principle for equilibrium states of Hölder potentials: the zero temperature case. Stoch. Dyn. 6 (2006), 77–96.Google Scholar
Batista, T., Gonschorowski, J. and Tal, F.. Density of the set of endomorphisms with a maximizing measure supported on a periodic orbit. Discrete Contin. Dyn. 35 (2015), 3315–3326.Google Scholar
Bawa, V. S.. Stochastic dominance: a research bibliography. Manag. Sci. 28 (1982), 698–712.Google Scholar
Bissacot, R. and Freire, R. Jr. On the existence of maximizing measures for irreducible countable Markov shifts: a dynamical proof. Ergod. Th. & Dynam. Sys. 34 (2014), 1103–1115.Google Scholar
Bissacot, R. and Garibaldi, E.. Weak KAM methods and ergodic optimal problems for countable Markov shifts. Bull. Braz. Math. Soc. (N.S.) 41 (2010), 321–338.Google Scholar
Bissacot, R., Garibaldi, E. and Thieullen, Ph.. Zero-temperature phase diagram for double-well type potentials in the summable variation class. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2016.57. Published online: 19 September 2016.Google Scholar
Blokh, A.. Functional rotation numbers for one dimensional maps. Trans. Amer. Math. Soc. 347 (1995), 499–513.Google Scholar
Blondel, V. D., Theys, J. and Vladimirov, A. A.. An elementary counterexample to the finiteness conjecture. SIAM J. Matrix Anal. Appl. 24 (2003), 963–970.Google Scholar
Bochi, J. and Morris, I. D.. Continuity properties of the lower spectral radius. Proc. Lond. Math. Soc. 110 (2015), 477–509.Google Scholar
Bochi, J. and Rams, M.. The entropy of Lyapunov-optimizing measures of some matrix cocycles. J. Mod. Dyn. 10 (2016), 255–286.Google Scholar
Bochi, J. and Zhang, Y.. Ergodic optimization of prevalent super-continuous functions. Int. Math. Res. Not. IMRN 19 (2016), 5988–6017.Google Scholar
Bohr, T. and Rand, D.. The entropy function for characteristic exponents. Physica D 25 (1986), 387–398.Google Scholar
Bousch, T.. Le poisson n’a pas d’arêtes. Ann. Inst. Henri Poincaré Probab. Stat. 36 (2000), 489–508.Google Scholar
Bousch, T.. La condition de Walters. Ann. Sci. ENS 34 (2001), 287–311.Google Scholar
Bousch, T.. Un lemme de Mañé bilatéral. C. R. Acad. Sci. Paris Sér. I 335 (2002), 533–536.Google Scholar
Bousch, T.. Nouvelle preuve d’un théorème de Yuan et Hunt. Bull. Soc. Math. France 126 (2008), 227–242.Google Scholar
Bousch, T.. Le lemme de Mañé-Conze-Guivarc’h pour les systèmes amphi-dynamiques rectifiables. Ann. Fac. Sci. Toulouse Math. 20 (2011), 1–14.Google Scholar
Bousch, T.. Genericity of minimizing periodic orbits, after Contreras. British Math. Colloq. talk. (April 2014), QMUL.Google Scholar
Bousch, T. and Jenkinson, O.. Cohomology classes of dynamically non-negative C k functions. Invent. Math. 148 (2002), 207–217.Google Scholar
Bousch, T. and Mairesse, J.. Asymptotic height optimization for topical IFS, Tetris heaps, and the finiteness conjecture. J. Amer. Math. Soc. 15 (2002), 77–111.Google Scholar
Bowen, R.. Topological entropy for noncompact sets. Trans. Amer. Math. Soc. 184 (1973), 125–136.Google Scholar
Branco, F.. Sub-actions and maximizing measures for one-dimensional transformations with a critical point. Discrete Cont. Dyn. Syst. 17 (2007), 271–280.Google Scholar
Branton, S.. Sub-actions for Young towers. Discrete Cont. Dyn. Syst. 22 (2008), 541–556.Google Scholar
Brémont, J.. On the behaviour of Gibbs measures at temperature zero. Nonlinearity 16 (2003), 419–426.Google Scholar
Brémont, J.. Finite flowers and maximizing measures for generic Lipschitz functions on the circle. Nonlinearity 19 (2006), 813–828.Google Scholar
Brémont, J.. Dynamics of injective quasi-contractions. Ergod. Th. & Dynam. Sys. 26 (2006), 19–44.Google Scholar
Brémont, J.. Entropy and maximizing measures of generic continuous functions. C. R. Math. Acad. Sci. Sér. I 346 (2008), 199–201.Google Scholar
Brémont, J. and Buczolich, Z.. Maximizing points and coboundaries for an irrational rotation on a circle. Ergod. Th. & Dynam. Sys. 33 (2013), 24–48.Google Scholar
Bressaud, X. and Quas, A.. Rate of approximation of minimizing measures. Nonlinearity 20 (2007), 845–853.Google Scholar
Bullett, S. and Sentenac, P.. Ordered orbits of the shift, square roots, and the devil’s staircase. Math. Proc. Camb. Phil. Soc. 115 (1994), 451–481.Google Scholar
Carlson, D. A., Haurie, A. B. and Leizarowitz, A.. Infinite Horizon Optimal Control: Deterministic and Stochastic Systems, 2nd edn. Springer, 1991.Google Scholar
Chazottes, J.-R., Gambaudo, J.M. and Ugalde, E.. Zero-temperature limit of one dimensional Gibbs states via renormalization: the case of locally constant potentials. Ergod. Th. & Dynam. Sys. 31 (2011), 1109–1161.Google Scholar
Chazottes, J.-R. and Hochman, M.. On the zero-temperature limit of Gibbs states. Comm. Math. Phys. 297 (2010), 265–281.Google Scholar
Chen, Y. and Zhao, Y.. Ergodic optimization for a sequence of continuous functions. Chinese J. Contemp. Math. 34 (2013), 351–360.Google Scholar
Coelho, Z. N.. Entropy and ergodicity of skew-products over subshifts of finite type and central limit asymptotics. PhD Thesis, Warwick University, 1990.Google Scholar
Collier, D. and Morris, I. D.. Approximating the maximum ergodic average via periodic orbits. Ergod. Th. & Dynam. Sys. 28 (2008), 1081–1090.Google Scholar
Contreras, G.. Ground states are generically a periodic orbit. Invent. Math. 205 (2016), 383–412.Google Scholar
Contreras, G., Lopes, A. O. and Thieullen, Ph.. Lyapunov minimizing measures for expanding maps of the circle. Ergod. Th. & Dynam. Sys. 21 (2001), 1379–1409.Google Scholar
Conze, J.-P. and Guivarc’h, Y.. Croissance des sommes ergodiques, Manuscript, circa 1993.Google Scholar
Coronel, D. and Rivera-Letelier, J.. Sensitive dependence of Gibbs measures at low temperatures. J. Stat. Phys. 160 (2015), 1658–1683.Google Scholar
Coronel, D. and Rivera-Letelier, J.. Sensitive dependence of geometric Gibbs states. Preprint, 2017,arXiv:1708.03965.Google Scholar
Daubechies, I. and Lagarias, J. C.. Sets of matrices all infinite products of which converge. Linear Algebra Appl. 162 (1992), 227–261.Google Scholar
Davie, A., Urbański, M. and Zdunik, A.. Maximizing measures of metrizable non-compact spaces. Proc. Edinb. Math. Soc. 50 (2007), 123–151.Google Scholar
Durand, B., Romashchenko, A. and Shen, A.. Fixed-point tile sets and their applications. J. Comput. System Sci. 78 (2012), 731–764.Google Scholar
van Enter, A. C. D. and Ruszel, W. M.. Chaotic temperature dependence at zero temperature. J. Stat. Phys. 127 (2007), 567–573.Google Scholar
Fathi, A.. Théorème KAM faible et théorie de Mather sur les systèmes lagrangiens. C. R. Acad. Sci. Paris Sér. I 324(9) (1997), 1043–1046.Google Scholar
Fathi, A.. Solutions KAM faibles conjuguées et barrières de Peierls. C. R. Acad. Sci. Paris Sér. I 325(6) (1997), 649–652.Google Scholar
Fathi, A.. Orbites hétéroclines et ensemble de Peierls. C. R. Acad. Sci. Paris Sér. I 326(10) (1998), 1213–1216.Google Scholar
Fathi, A.. Sur la convergence du semi-groupe de Lax-Oleinik. C. R. Acad. Sci. Paris Sér. I 327(3) (1998), 267–270.Google Scholar
Freire, R. and Vargas, V.. Equilibrium states and zero temperature limit on topologically transitive countable Markov shifts. Trans. Amer. Math. Soc. Preprint, 2015, arXiv:1511.01527, to appear, doi:10.1090/tran/7291.Google Scholar
Garibaldi, E. and Gomes, J. T. A.. Aubry set for asymptotically sub-additive potentials. Stoch. Dyn. 16 (2016), 1660009.Google Scholar
Garibaldi, E. and Lopes, A. O.. Functions for relative maximization. Dyn. Syst. 22 (2007), 511–528.Google Scholar
Garibaldi, E. and Lopes, A. O.. On Aubry–Mather theory for symbolic dynamics. Ergod. Th. & Dynam. Sys. 28 (2008), 791–815.Google Scholar
Garibaldi, E., Lopes, A. O. and Thieullen, Ph.. On calibrated and separating sub-actions. Bull. Braz. Math. Soc. (N.S.) 40 (2009), 577–602.Google Scholar
Garibaldi, E. and Thieullen, Ph.. Description of some ground states by Puiseux techniques. J. Stat. Phys. 146 (2012), 125–180.Google Scholar
Geller, W. and Misiurewicz, M.. Rotation and entropy. Trans. Amer. Math. Soc. 351 (1999), 2927–2948.Google Scholar
Halsey, T. C., Jensen, M. H., Kadanoff, L. P., Procaccia, I and Shraiman, B. J.. Fractal measures and their singularities: the characterization of strange sets. Phys. Rev. A 33 (1986), 1141–1151.Google Scholar
Hare, K. G., Morris, I.  D., Sidorov, N. and Theys, J.. An explicit counterexample to the Lagarias–Wang finiteness conjecture. Adv. Math. 226 (2011), 4667–4701.Google Scholar
Harriss, E. and Jenkinson, O.. Flattening functions on flowers. Ergod. Th. & Dynam. Sys. 27 (2007), 1865–1886.Google Scholar
Hentschel, H. and Procaccia, I.. The infinite number of generalized dimensions of fractals and strange attractors. Physica D 8 (1983), 435–444.Google Scholar
Hochman, M.. On the dynamics and recursive properties of multidimensional symbolic systems. Invent. Math. 176 (2009), 131–167.Google Scholar
Hunt, B. R. and Ott, E.. Optimal periodic orbits of chaotic systems. Phys. Rev. Lett. 76 (1996), 2254–2257.Google Scholar
Hunt, B. R. and Ott, E.. Optimal periodic orbits of chaotic systems occur at low period. Phys. Rev. E 54 (1996), 328–337.Google Scholar
Hunt, B. R., Sauer, T. and Yorke, J. A.. Prevalence: a translation-invariant ‘almost every’ on infinite-dimensional spaces. Bull Amer. Math. Soc. (N.S.) 27 (1992), 217–238.Google Scholar
Iommi, G.. Ergodic optimization for renewal type shifts. Monatsh. Math. 150 (2007), 91–95.Google Scholar
Iommi, G. and Todd, M.. Natural equilibrium states for multimodal maps. Comm. Math. Phys. 300 (2010), 65–94.Google Scholar
Iommi, G. and Yayama, Y.. Zero temperature limits of Gibbs states for almost-additive potentials. J. Stat. Phys. 155 (2014), 23–46.Google Scholar
Jenkinson, O.. Conjugacy rigidity, cohomological triviality, and barycentres of invariant measures. PhD Thesis, Warwick University, 1996.Google Scholar
Jenkinson, O.. Frequency locking on the boundary of the barycentre set. Exp. Math. 9 (2000), 309–317.Google Scholar
Jenkinson, O.. Geometric barycentres of invariant measures for circle maps. Ergod. Th. & Dynam. Sys. 21 (2001), 511–532.Google Scholar
Jenkinson, O.. Directional entropy of rotation sets. C. R. Acad. Sci. Paris Sér. I 332 (2001), 921–926.Google Scholar
Jenkinson, O.. Rotation, entropy, and equilibrium states. Trans. Amer. Math. Soc. 353 (2001), 3713–3739.Google Scholar
Jenkinson, O.. Maximum hitting frequency and fastest mean return time. Nonlinearity 18 (2005), 2305–2321.Google Scholar
Jenkinson, O.. Ergodic optimization. Discrete Contin. Dyn. Syst. 15 (2006), 197–224.Google Scholar
Jenkinson, O.. Every ergodic measure is uniquely maximizing. Discrete Contin. Dyn. Syst. 16 (2006), 383–392.Google Scholar
Jenkinson, O.. Optimization and majorization of invariant measures. Electron. Res. Announc. Amer. Math. Soc. 13 (2007), 1–12.Google Scholar
Jenkinson, O.. A partial order on × 2-invariant measures. Math. Res. Lett. 15 (2008), 893–900.Google Scholar
Jenkinson, O.. On sums of powers of inverse complete quotients. Proc. Amer. Math. Soc. 136 (2008), 1023–1027.Google Scholar
Jenkinson, O.. Balanced words and majorization. Discrete Math. Algorithms Appl. 1 (2009), 463–483.Google Scholar
Jenkinson, O., Mauldin, R. D. and Urbański, M.. Zero temperature limits of Gibbs-equilibrium states for countable alphabet subshifts of finite type. J. Stat. Phys. 119 (2005), 765–776.Google Scholar
Jenkinson, O., Mauldin, R. D. and Urbański, M.. Ergodic optimization for countable alphabet subshifts of finite type. Ergod. Th. & Dynam. Sys. 26 (2006), 1791–1803.Google Scholar
Jenkinson, O., Mauldin, R. D. and Urbański, M.. Ergodic optimization for non-compact dynamical systems. Dyn. Sys. 22 (2007), 379–388.Google Scholar
Jenkinson, O. and Morris, I. D.. Lyapunov optimizing measures for C 1 expanding maps of the circle. Ergod. Th. & Dynam. Sys. 28 (2008), 1849–1860.Google Scholar
Jenkinson, O. and Pollicott, M.. Joint spectral radius, Sturmian measures, and the finiteness conjecture. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2017.18. Published online: 02 May 2017.Google Scholar
Jenkinson, O. and Steel, J.. Majorization of invariant measures for orientation-reversing maps. Ergod. Th. & Dynam. Sys. 30 (2010), 1471–1483.Google Scholar
Jungers, R.. The Joint Spectral Radius (Lecture Notes in Control and Information Sciences, 385) . Springer, Berlin, 2009.Google Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press, Cambridge, 1995.Google Scholar
Keller, G.. Equilibrium States in Ergodic Theory. Cambridge University Press, Cambridge, 1998.Google Scholar
Kempton, T.. Zero temperature limits of Gibbs equilibrium states for countable Markov shifts. J. Stat. Phys. 143 (2011), 795–806.Google Scholar
Kertz, R. P. and Rösler, U.. Stochastic and convex orders and lattices of probability measures, with a Martingale interpretation. Israel J. Math. 77 (1992), 129–164.Google Scholar
Kucherenko, T. and Wolf, C.. Geometry and entropy of generalized rotation sets. Israel J. Math. 199 (2014), 791–829.Google Scholar
Kucherenko, T. and Wolf, C.. Ground states and zero-temperature measures at the boundary of rotation sets. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2017.27. Published online: 02 May 2017.Google Scholar
Lagarias, J. C. and Wang, Y.. The finiteness conjecture for the generalized spectral radius of a set of matrices. Linear Algebra Appl. 214 (1995), 17–42.Google Scholar
Lanford, O. E.. Entropy and Equilibrium States in Classical Statistical Mechanics (Springer Lecture Notes in Physics, 20) . Ed. Lenard, A.. Springer, Berlin, 1973, pp. 1–113.Google Scholar
Leplaideur, R.. A dynamical proof for convergence of Gibbs measures at temperature zero. Nonlinearity 18 (2005), 2847–2880.Google Scholar
Leplaideur, R.. Flatness is a criterion for selection of maximizing measures. J. Stat. Phys. 147 (2012), 728–757.Google Scholar
Livšic, A.. Homology properties of Y-systems. Math. Zametki 10 (1971), 758–763.Google Scholar
Lopes, A. O. and Mengue, J.. Zeta measures and thermodynamic formalism for temperature zero. Bull. Braz. Math. Soc. (N.S.) 41 (2010), 321–338.Google Scholar
Lopes, A. O. and Mengue, J.. Selection of measure and a large deviation principle for the general one-dimensional XY model. Dynam. Syst. 29 (2014), 24–39.Google Scholar
Lopes, A. O., Mohr, J., Souza, R. and Thieullen, Ph.. Negative entropy, zero temperature and Markov chains on the interval. Bull. Braz. Math. Soc. (N.S.) 40 (2009), 1–52.Google Scholar
Lopes, A. O., Rosas, V. and Ruggiero, R.. Cohomology and subcohomology problems for expansive, non Anosov geodesic flows. Discrete Contin. Dyn. Syst. 17 (2007), 403–422.Google Scholar
Lopes, A. O. and Thieullen, Ph.. Sub-actions for Anosov diffeomorphisms. Geometric Methods in Dynamics II. Astérisque 287 (2003), 135–146.Google Scholar
Lopes, A. O. and Thieullen, Ph.. Sub-actions for Anosov flows. Ergod. Th. & Dynam. Sys. 25 (2005), 605–628.Google Scholar
Lopes, A. O. and Thieullen, Ph.. Mather measures and the Bowen-Series transformation. Ann. Inst. H. Poincaré Anal. Non Linéaire 23 (2006), 663–682.Google Scholar
Mañé, R.. On the minimizing measures of Lagrangian dynamical systems. Nonlinearity 5 (1992), 623–638.Google Scholar
Mañé, R.. Generic properties and problems of minimizing measures of Lagrangian systems. Nonlinearity 9 (1996), 273–310.Google Scholar
Marshall, A. W. and Olkin, I.. Inequalities: Theory of Majorization and its Applications (Mathematics in Science and Engineering, 143) . Academic Press, New York, 1979.Google Scholar
Mauldin, R. D. and Urbański, M.. Graph Directed Markov Systems: Geometry and Dynamics of Limit Sets. Cambridge University Press, Cambridge, 2003.Google Scholar
McGoff, K. and Nobel, A. B.. Optimal tracking for dynamical systems. Preprint, 2016, arXiv:1601.05033.Google Scholar
Morita, T. and Tokunaga, Y.. Measures with maximum total exponent and generic properties of C 1 expanding maps. Hiroshima Math. J. 43 (2013), 351–370.Google Scholar
Morris, I. D.. Entropy for zero-temperature limits of Gibbs-equilibrium states for countable-alphabet subshifts of finite type. J. Stat. Phys. 126 (2007), 315–324.Google Scholar
Morris, I. D.. A sufficient condition for the subordination principle in ergodic optimization. Bull. Lond. Math. Soc. 39 (2007), 214–220.Google Scholar
Morris, I. D.. Maximizing measures of generic Hölder functions have zero entropy. Nonlinearity 21 (2008), 993–1000.Google Scholar
Morris, I. D.. The Mañé–Conze–Guivarc’h lemma for intermittent maps of the circle. Ergod. Th. & Dynam. Sys. 29 (2009), 1603–1611.Google Scholar
Morris, I. D.. Ergodic optimization for generic continuous functions. Discrete Contin. Dyn. Syst. 27 (2010), 383–388.Google Scholar
Morris, I. D.. Criteria for the stability of the finiteness property and for the uniqueness of Barabanov norms. Linear Algebra Appl. 443 (2010), 1301–1311.Google Scholar
Morris, I. D.. A rapidly-converging lower bound for the joint spectral radius via multiplicative ergodic theory. Adv. Math. 225 (2010), 3425–3445.Google Scholar
Morris, I. D.. The generalised Berger–Wang formula and the spectral radius of linear cocycles. J. Funct. Anal. 262 (2012), 811–824.Google Scholar
Morris, I. D.. Mather sets for sequences of matrices and applications to the study of joint spectral radii. Proc. Lond. Math. Soc. 107 (2013), 121–150.Google Scholar
Morris, I. D. and Sidorov, N.. On a devil’s staircase associated to the joint spectral radii of a family of pairs of matrices. J. Eur. Math. Soc. (JEMS) 15 (2013), 1747–1782.Google Scholar
Morse, M. and Hedlund, G. A.. Symbolic dynamics II. Sturmian trajectories. Amer. J. Math. 62 (1940), 1–42.Google Scholar
Newhouse, S.. Continuity properties of entropy. Ann. of Math. (2) 129 (1989), 215–235.Google Scholar
Pesin, Ya.. Dimension Theory in Dynamical Systems. University of Chicago Press, Chicago, IL, 1997.Google Scholar
Pesin, Ya. and Pitskel’, B.. Topological pressure and the variational principle for noncompact sets. Funct. Anal. Appl. 18 (1984), 307–318.Google Scholar
Parry, W.. Handwritten notes on zero temperature limits of equilibrium states, circa 1990.Google Scholar
Parry, W. and Pollicott, M.. Zeta functions and the periodic orbit structure of hyperbolic dynamics. Astérisque 187–188 (1990), 1–268.Google Scholar
Pollicott, M. and Sharp, R.. Rates of recurrence for ℤ q and ℝ q extensions of subshifts of finite type. J. Lond. Math. Soc. 49 (1994), 401–416.Google Scholar
Pollicott, M. and Sharp, R.. Livsic theorems, maximizing measures and the stable norm. Dyn. Syst. 19 (2004), 75–88.Google Scholar
Quas, A. and Siefken, J.. Ergodic optimization of supercontinuous functions on shift spaces. Ergod. Th. & Dyn. Syst. 32 (2012), 2071–2082.Google Scholar
Rota, G.-C. and Strang, G.. A note on the joint spectral radius. Indag. Math. 22 (1960), 379–381.Google Scholar
Ruelle, D.. Thermodynamic Formalism. Addison-Wesley, Reading, MA, 1978.Google Scholar
Savchenko, S. V.. Homological inequalities for finite topological Markov chains. Funct. Anal. Appl. 33 (1999), 236–238.Google Scholar
Schmeling, J.. On the completeness of multifractal spectra. Ergod. Th. & Dynam. Sys. 19 (1999), 1595–1616.Google Scholar
Shaked, M. and Shanthikumar, J. G.. Stochastic Orders. Springer, New York, 2007.Google Scholar
Sigmund, K.. Generic properties of invariant measures for Axiom A diffeomorphisms. Invent. Math. 11 (1970), 99–109.Google Scholar
Souza, R.. Sub-actions for weakly hyperbolic one-dimensional systems. Dyn. Syst. 18 (2003), 165–179.Google Scholar
Steel, J.. Concave unimodal maps have no majorisation relations between their ergodic measures. Proc. Amer. Math. Soc. 139 (2011), 2553–2558.Google Scholar
Sturman, R. and Stark, J.. Semi-uniform ergodic theorems and applications to forced systems. Nonlinearity 13 (2000), 113–143.Google Scholar
Takahasi, H.. Equilibrium measures at temperature zero for Hénon-like maps at the first bifurcation. SIAM J. Appl. Dyn. Syst. 15 (2016), 106–124.Google Scholar
Tal, F. A. and Addas-Zanata, S.. On maximizing measures of homeomorphisms on compact manifolds. Fund. Math. 200 (2008), 145–159.Google Scholar
Tal, F. A. and Addas-Zanata, S.. Maximizing measures for endomorphisms of the circle. Nonlinearity 21 (2008), 2347–2359.Google Scholar
Veerman, P.. Symbolic dynamics of order-preserving orbits. Physica D 29 (1987), 191–201.Google Scholar
Walters, P.. Invariant measures and equilibrium states for some mappings which expand distances. Trans. Amer. Math. Soc. 236 (1978), 127–153.Google Scholar
Walters, P.. An Introduction to Ergodic Theory. Springer, New York, 1981.Google Scholar
Yang, T.-H., Hunt, B. R. and Ott, E.. Optimal periodic orbits of continuous time chaotic systems. Phys. Rev. E 62 (2000), 1950–1959.Google Scholar
Yuan, G. and Hunt, B. R.. Optimal orbits of hyperbolic systems. Nonlinearity 12 (1999), 1207–1224.Google Scholar
Ziemian, K.. Rotation sets for subshifts of finite type. Fund. Math. 146 (1995), 189–201.Google Scholar
Zhao, Y.. Conditional ergodic averages for asymptotically additive potentials. Preprint, 2014,arXiv:1405.1648.Google Scholar
Zhao, Y.. Maximal integral over observable measures. Acta Math. Sinica 32 (2016), 571–578.Google Scholar