Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-28T15:41:15.377Z Has data issue: false hasContentIssue false
  • English
  • Français

Ergodicity of Iwasawa continued fractions via markable hyperbolic geodesics

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Ergodic theory Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  28 March 2022

ANTON LUKYANENKO Open the ORCID record for ANTON LUKYANENKO [Opens in a new window]  and
JOSEPH VANDEHEY
ANTON LUKYANENKO*
Affiliation:
Department of Mathematics, George Mason University, 4400 University Drive, MS: 3F2, Fairfax, VA 22030, USA
JOSEPH VANDEHEY
Affiliation:
Department of Mathematics, University of Texas at Tyler, Tyler, TX 75799, USA (e-mail: jvandehey@uttyler.edu)
*
e-mail: anton@lukyanenko.net
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove the convergence and ergodicity of a wide class of real and higher-dimensional continued fraction algorithms, including folded and 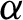$\alpha $ -type variants of complex, quaternionic, octonionic, and Heisenberg continued fractions, which we combine under the framework of Iwasawa continued fractions. The proof is based on the interplay of continued fractions and hyperbolic geometry, the ergodicity of geodesic flow in associated modular manifolds, and a variation on the notion of geodesic coding that we refer to as geodesic marking. As a corollary of our study of markable geodesics, we obtain a generalization of Serret’s tail-equivalence theorem for almost all points. The results are new even in the case of some real and complex continued fractions.

Keywords

continued fractionsgeodesic codingergodicitycomplex continued fractionsIwasawa continued fractionsHeisenberg continued fractions

MSC classification

Primary: 37D40: Dynamical systems of geometric origin and hyperbolicity (geodesic and horocycle flows, etc.)
Secondary: 11K50: Metric theory of continued fractions 37A45: Relations with number theory and harmonic analysis
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 5 , May 2023 , pp. 1666 - 1711
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, R. L. and Flatto, L.. The backward continued fraction map and geodesic flow. Ergod. Th. & Dynam. Sys. 4(4) (1984), 487–492.CrossRefGoogle Scholar
Arnoux, P. and Schmidt, T. A.. Cross sections for geodesic flows and $\alpha$ -continued fractions. Nonlinearity 26(3) (2013), 711–726.CrossRefGoogle Scholar
Artin, E.. Ein mechanisches system mit quasiergodischen bahnen [A mechanical system with quasiergodic orbits]. Abh. Math. Semin. Univ. Hambg. 3(1) (1924), 170–175.Google Scholar
Bauer, M. and Lopes, A.. A billiard in the hyperbolic plane with decay of correlation of type ${n}^{-2}$ . Discrete Contin. Dyn. Syst. 3(1) (1997), 107–116.CrossRefGoogle Scholar
Boca, F. P. and Merriman, C.. Coding of geodesics on some modular surfaces and applications to odd and even continued fractions. Indag. Math. (N.S.) 29(5) (2018), 1214–1234.CrossRefGoogle Scholar
Burton, R., Kraaikamp, C. and Schmidt, T.. Natural extensions for the Rosen fractions. Trans. Amer. Math. Soc. 352(3) (2000), 1277–1298.CrossRefGoogle Scholar
Calta, K. and Schmidt, T. A.. Continued fractions for a class of triangle groups. J. Aust. Math. Soc. 93(1–2) (2012), 21–42.CrossRefGoogle Scholar
Cao, W. and Parker, J. R.. Shimizu’s lemma for quaternionic hyperbolic space. Comput. Methods Funct. Theory 18(1) (2018), 159–191.CrossRefGoogle Scholar
Chousionis, V., Tyson, J. and Urbański, M.. Conformal graph directed Markov systems on Carnot groups. Mem. Amer. Math. Soc. 266(1291) (2020), viii+155.Google Scholar
Cijsouw, B.. Complex continued fraction algorithms. Master’s Thesis, Radboud University, 2015.Google Scholar
Conway, J. H. and Smith, D. A.. On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry. A K Peters, Ltd., Natick, MA, 2003.CrossRefGoogle Scholar
Cowling, M., Dooley, A. H., Korányi, A. and Ricci, F.. H-type groups and Iwasawa decompositions. Adv. Math. 87(1) (1991), 1–41.CrossRefGoogle Scholar
Dajani, K., Hensley, D., Kraaikamp, C. and Masarotto, V.. Arithmetic and ergodic properties of ‘flipped’ continued fraction algorithms. Acta Arith. 153(1) (2012), 51–79.CrossRefGoogle Scholar
Dajani, K. and Kraaikamp, C.. Ergodic Theory of Numbers (Carus Mathematical Monographs, 29). American Mathematical Society, Providence, RI, 2002.CrossRefGoogle Scholar
Dajani, K., Kraaikamp, C. and Steiner, W.. Metrical theory for $\alpha$ -Rosen fractions. J. Eur. Math. Soc. (JEMS) 11(6) (2009), 1259–1283.CrossRefGoogle Scholar
Dajani, K., Kraaikamp, C. and van der Wekken, N.. Ergodicity of $N$ -continued fraction expansions. J. Number Theory 133(9) (2013), 3183–3204.Google Scholar
Dani, S. G.. Continued fraction expansions for complex numbers—a general approach. Acta Arith. 171(4) (2015), 355–369.CrossRefGoogle Scholar
Ei, H., Ito, S., Nakada, H. and Natsui, R.. On the construction of the natural extension of the Hurwitz complex continued fraction map. Monatsh. Math. 188(1) (2019), 37–86.CrossRefGoogle Scholar
Einsiedler, M. and Ward, T.. Ergodic Theory with a View Towards Number Theory (Graduate Texts in Mathematics, 259). Springer-Verlag, London, 2011.CrossRefGoogle Scholar
Gröchenig, K. and Haas, A.. Backward continued fractions, Hecke groups and invariant measures for transformations of the interval. Ergod. Th. & Dynam. Sys. 16(6) (1996), 1241–1274.Google Scholar
Goldman, W. M.. Complex Hyperbolic Geometry (Oxford Mathematical Monographs). Oxford Science Publications; The Clarendon Press; Oxford University Press, New York, 1999.Google Scholar
Hamilton, W. R.. On continued fractions in quaternions. Philos. Mag. III (1852), 371–373; IV (1852), 303; V (1853), 117–118, 236–238, 321–326.CrossRefGoogle Scholar
Hamilton, W. R.. On the connexion of quaternions with continued fractions and quadratic equations. Proc. R. Ir. Acad. 5(219–221) (1853), 299–301.Google Scholar
Hayward, G. P.. The action of the Picard group on hyperbolic 3-space and complex continued fractions. PhD Thesis, University of the Witwatersrand, Faculty of Science, School of Mathematics, 2014.Google Scholar
Hedlund, G. A.. A metrically transitive group defined by the modular groups. Amer. J. Math. 57(3) (1935), 668–678.CrossRefGoogle Scholar
Hensley, D.. Continued Fractions. World Scientific, Hackensack, NJ, 2006.CrossRefGoogle Scholar
Hersonsky, S. and Paulin, F.. Diophantine approximation for negatively curved manifolds. Math. Z. 241(1) (2002), 181–226.CrossRefGoogle Scholar
Hiary, G. and Vandehey, J.. Calculations of the invariant measure for Hurwitz continued fractions. Exp. Math. doi: 10.1080/10586458.2019.1627255. Published online 26 June 2019.Google Scholar
Hines, R.. Badly approximable numbers over imaginary quadratic fields. Acta Arith. 190(2) (2019), 101–125.CrossRefGoogle Scholar
Hurwitz, A.. Uber die Entwicklung complexer Grössen in Kettenbrüche [On the expansion of complex quantities in continued fractions]. Acta Math. 11(1–4) (1887), 187–200.CrossRefGoogle Scholar
Hurwitz, A.. Uber eine besondere Art der Kettenbruch-Entwicklung reeller Grössen [On a special type of continued fraction expansions of real numbers]. Acta Math. 12(1) (1889), 367–405.CrossRefGoogle Scholar
Ito, S. and Yuri, M.. Number theoretical transformations with finite range structure and their ergodic properties. Tokyo J. Math. 10 (1987), 1–32.CrossRefGoogle Scholar
Katok, S. and Ugarcovici, I.. Arithmetic coding of geodesics on the modular surface via continued fractions. European Women in Mathematics—Marseille 2003 (CWI Tract, 135). Eds. K. Dajani and J. von Reis. Centrum Wiskunde & Informatica, Amsterdam, 2005, pp. 59–77.Google Scholar
Katok, S. and Ugarcovici, I.. Symbolic dynamics for the modular surface and beyond. Bull. Amer. Math. Soc. (N.S.) 44(1) (2007), 87–132.CrossRefGoogle Scholar
Katok, S. and Ugarcovici, I.. Applications of $\left(a,b\right)$ -continued fraction transformations. Ergod. Th. & Dynam. Sys. 32(2) (2012), 755–777.CrossRefGoogle Scholar
Lakein, R. B.. Continued fractions and equivalent complex numbers. Proc. Amer. Math. Soc. 42 (1974), 641–642.Google Scholar
Le Donne, E.. A metric characterization of Carnot groups. Proc. Amer. Math. Soc. 143(2) (2015), 845–849.CrossRefGoogle Scholar
Lukyanenko, A. and Vandehey, J.. Continued fractions on the Heisenberg group. Acta Arith. 167(1) (2015), 19–42.CrossRefGoogle Scholar
Lukyanenko, A. and Vandehey, J.. Intrinsic diophantine approximation in Carnot groups and in the Siegel model of the Heisenberg group. Monatsh. Math. 192(3) (2020), 651–676.CrossRefGoogle Scholar
Marmi, S., Moussa, P. and Yoccoz, J.-C.. The Brjuno functions and their regularity properties. Comm. Math. Phys. 186(2) (1997), 265–293.CrossRefGoogle Scholar
Masarotto, V.. Metric and arithmetic properties of a new class of continued fraction expansions. Master’s Thesis, Universita di Padova and Leiden University, 2009.Google Scholar
Mautner, F. I.. Geodesic flows on symmetric Riemann spaces. Ann. of Math. (2) 65 (1957), 416–431.CrossRefGoogle Scholar
Mayer, D. and Strömberg, F.. Symbolic dynamics for the geodesic flow on Hecke surfaces. J. Mod. Dyn. 2(4) (2008), 581–627.CrossRefGoogle Scholar
Mennen, C. M.. The algebra and geometry of continued fractions with integer quaternion coefficients. PhD Thesis, University of the Witwatersrand, 2015.Google Scholar
Nakada, H.. On the Kuzmin’s theorem for the complex continued fractions. Keio Engrg. Rep. 29(9) (1976), 93–108.Google Scholar
Nakada, H.. Metrical theory for a class of continued fraction transformations and their natural extensions. Tokyo J. Math. 4(2) (1981), 399–426.CrossRefGoogle Scholar
Nakada, H.. On ergodic theory of A. Schmidt’s complex continued fractions over Gaussian field. Monatsh. Math. 105(2) (1988), 131–150.CrossRefGoogle Scholar
Nakada, H. and Natsui, R.. On the equivalence relations of $\alpha$ -continued fractions. Indag. Math. (N.S.) 25(4) (2014), 800–815.CrossRefGoogle Scholar
Nakada, H. and Steiner, W.. On the ergodic theory of Tanaka–Ito type $\alpha$ -continued fractions. Tokyo J. Math. 1(1) (2021), 1–15.Google Scholar
Panti, G.. Slow continued fractions, transducers, and the Serret theorem. J. Number Theory 185 (2018), 121–143.CrossRefGoogle Scholar
Parker, J. R.. Shimizu’s lemma for complex hyperbolic space. Internat. J. Math. 3(2) (1992), 291–308.CrossRefGoogle Scholar
Pollicott, M.. The Picard group, closed geodesics and zeta functions. Trans. Amer. Math. Soc. 344(2) (1994), 857–872.Google Scholar
Schmidt, A. L.. Diophantine approximation of complex numbers. Acta Math. 134(1) (1975), 1–85.CrossRefGoogle Scholar
Schweiger, F.. Ergodic Theory of Fibred Systems and Metric Number Theory. Oxford Science Publications; The Clarendon Press; Oxford University Press, New York, 1995.Google Scholar
Schweiger, F.. Multidimensional Continued Fractions. Oxford University Press, New York, 2000.Google Scholar
Schweiger, F. and Waterman, M.. Some remarks on Kuzmin’s theorem for F-expansions. J. Number Theory 5(2) (1973), 123–131.CrossRefGoogle Scholar
Series, C.. The modular surface and continued fractions. J. Lond. Math. Soc. (2) 31(1) (1985), 69–80.CrossRefGoogle Scholar
Shiokawa, I., Kaneiwa, R. and Tamura, J.. A proof of Perron’s theorem on Diophantine approximation of complex numbers. Keio Engrg. Rep. 28(12) (1975), 131–147.Google Scholar
Śleszyński, I.. Supplement to the Note on the Convergence of Continued Fractions. Mathematical Collection 14(3) (1889), 436–438 (in Russian).Google Scholar
Tanaka, S.. A complex continued fraction transformation and its ergodic properties. Tokyo J. Math. 8(1) (1985), 191–214.CrossRefGoogle Scholar
Tanaka, S. and Ito, S.. On a family of continued-fraction transformations and their ergodic properties. Tokyo J. Math. 4(1) (1981), 153–175.Google Scholar
Thurston, W.. Geometry and Topology of Three-Manifolds. Princeton University Press, Princeton, NJ, 1980.Google Scholar
Vandehey, J.. Lagrange’s theorem for continued fractions on the Heisenberg group. Bull. Lond. Math. Soc. 47(5) (2015), 866–882.CrossRefGoogle Scholar
Vandehey, J.. Non-trivial matrix actions preserve normality for continued fractions. Compos. Math. 153(2) (2017), 274–293.CrossRefGoogle Scholar
Zimmer, R. J.. Ergodic Theory and Semisimple Groups (Monographs in Mathematics, 81). Birkhäuser Verlag, Basel, 1984.CrossRefGoogle Scholar