Article contents
Extensive bounds on the topological entropy of repellers in piecewise expanding coupled map lattices
Published online by Cambridge University Press: 17 April 2012
Abstract
Beyond the uncoupled regime, the rigorous description of the dynamics of (piecewise) expanding coupled map lattices remains largely incomplete. To address this issue, we study repellers of periodic chains of linearly coupled Lorenz-type maps which we analyze by means of symbolic dynamics. Whereas all symbolic codes are admissible for sufficiently small coupling intensity, when the interaction strength exceeds a chain length independent threshold, we prove that a large bunch of codes is pruned and an extensive decay follows suit for the topological entropy. This quantity, however, does not immediately drop off to 0. Instead, it is shown to be continuous at the threshold and to remain extensively bounded below by a positive number in a large part of the expanding regime. The analysis is firstly accomplished in a piecewise affine setting where all calculations are explicit and is then extended by continuation to coupled map lattices based on 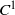 $C^1$-perturbations of the individual map.
$C^1$-perturbations of the individual map.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © 2012 Cambridge University Press
References
- 3
- Cited by

