Article contents
Flat strips, Bowen–Margulis measures, and mixing of the geodesic flow for rank one CAT(0) spaces
Published online by Cambridge University Press: 28 December 2015
Abstract
Let 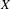 $X$ be a proper, geodesically complete CAT(
$X$ be a proper, geodesically complete CAT(  $0$ ) space under a proper, non-elementary, isometric action by a group
$0$ ) space under a proper, non-elementary, isometric action by a group 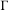 $\unicode[STIX]{x1D6E4}$ with a rank one element. We construct a generalized Bowen–Margulis measure on the space of unit-speed parametrized geodesics of
$\unicode[STIX]{x1D6E4}$ with a rank one element. We construct a generalized Bowen–Margulis measure on the space of unit-speed parametrized geodesics of  $X$ modulo the
$X$ modulo the 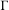 $\unicode[STIX]{x1D6E4}$ -action. Although the construction of Bowen–Margulis measures for rank one non-positively curved manifolds and for CAT(
$\unicode[STIX]{x1D6E4}$ -action. Although the construction of Bowen–Margulis measures for rank one non-positively curved manifolds and for CAT( 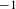 $-1$ ) spaces is well known, the construction for CAT(
$-1$ ) spaces is well known, the construction for CAT(  $0$ ) spaces hinges on establishing a new structural result of independent interest: almost no geodesic, under the Bowen–Margulis measure, bounds a flat strip of any positive width. We also show that almost every point in
$0$ ) spaces hinges on establishing a new structural result of independent interest: almost no geodesic, under the Bowen–Margulis measure, bounds a flat strip of any positive width. We also show that almost every point in 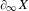 $\unicode[STIX]{x2202}_{\infty }X$ , under the Patterson–Sullivan measure, is isolated in the Tits metric. (For these results we assume the Bowen–Margulis measure is finite, as it is in the cocompact case.) Finally, we precisely characterize mixing when
$\unicode[STIX]{x2202}_{\infty }X$ , under the Patterson–Sullivan measure, is isolated in the Tits metric. (For these results we assume the Bowen–Margulis measure is finite, as it is in the cocompact case.) Finally, we precisely characterize mixing when 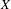 $X$ has full limit set: a finite Bowen–Margulis measure is not mixing under the geodesic flow precisely when
$X$ has full limit set: a finite Bowen–Margulis measure is not mixing under the geodesic flow precisely when 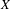 $X$ is a tree with all edge lengths in
$X$ is a tree with all edge lengths in 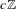 $c\mathbb{Z}$ for some
$c\mathbb{Z}$ for some 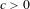 $c>0$ . This characterization is new, even in the setting of CAT(
$c>0$ . This characterization is new, even in the setting of CAT(  $-1$ ) spaces. More general (technical) versions of these results are also stated in the paper.
$-1$ ) spaces. More general (technical) versions of these results are also stated in the paper.
Information
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2015
References
- 14
- Cited by

