Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Feres, Renato
and
Katok, Anatoly
1989.
Invariant tensor fields of dynamical systems with pinched Lyapunov exponents and rigidity of geodesic flows.
Ergodic Theory and Dynamical Systems,
Vol. 9,
Issue. 3,
p.
427.
Kanai, Masahiko
1989.
A pinching theorem for cusps of negatively curved manifolds with finite volume.
Proceedings of the American Mathematical Society,
Vol. 107,
Issue. 3,
p.
777.
Feres, Renato
and
Katok, Anatole
1990.
Anosov flows with smooth foliations and rigidity of geodesic flows on three-dimensional manifolds of negative curvature.
Ergodic Theory and Dynamical Systems,
Vol. 10,
Issue. 4,
p.
657.
Hurder, S.
and
Katok, A.
1990.
Differentiability, rigidity and Godbillon-Vey classes for Anosov flows.
Publications mathématiques de l'IHÉS,
Vol. 72,
Issue. 1,
p.
5.
Hamenstādt, Ursula
1991.
Global Differential Geometry and Global Analysis.
Vol. 1481,
Issue. ,
p.
73.
Feres, Renato
1991.
Geodesic flows on manifolds of negative curvature with smooth horospheric foliations.
Ergodic Theory and Dynamical Systems,
Vol. 11,
Issue. 4,
p.
653.
Flaminio, L.
and
Katok, A.
1991.
Rigidity of symplectic Anosov diffeomorphisms on low dimensional tori.
Ergodic Theory and Dynamical Systems,
Vol. 11,
Issue. 3,
p.
427.
Benoist, Yves
Foulon, Patrick
and
Labourie, François
1992.
Flots d’Anosov à distributions stable et instable différentiables.
Journal of the American Mathematical Society,
Vol. 5,
Issue. 1,
p.
33.
KANAI, Masahiko
1993.
Differential-geometric studies on dynamics of geodesic and frame flows.
Japanese journal of mathematics. New series,
Vol. 19,
Issue. 1,
p.
1.
Hamenstädt, Ursula
1993.
Regularity of time-preserving conjugacies for contact Anosov flows withC1-Anosov splitting.
Ergodic Theory and Dynamical Systems,
Vol. 13,
Issue. 1,
p.
65.
Ghys, Étienne
1993.
Rigidité différentiable des groupes fuchsiens.
Publications mathématiques de l'IHÉS,
Vol. 78,
Issue. 1,
p.
163.
Hamenstädt, Ursula
1994.
Regularity at infinity of compact negatively curved manifolds.
Ergodic Theory and Dynamical Systems,
Vol. 14,
Issue. 3,
p.
493.
Hasselblatt, Boris
1994.
Regularity of the Anosov splitting and of horospheric foliations.
Ergodic Theory and Dynamical Systems,
Vol. 14,
Issue. 4,
p.
645.
Juhl, Andreas
1995.
Secondary invariants and the singularity of the Ruelle zeta-function in the central critical point.
Bulletin of the American Mathematical Society,
Vol. 32,
Issue. 1,
p.
80.
Hamenstädt, Ursula
1995.
Invariant two-forms for geodesic flows.
Mathematische Annalen,
Vol. 301,
Issue. 1,
p.
677.
Zeghib, Abdelghani
1996.
Killing fields in compact Lorentz {3}-manifolds.
Journal of Differential Geometry,
Vol. 43,
Issue. 4,
Cruceanu, V.
Fortuny, P.
and
Gadea, P.M.
1996.
A Survey on Paracomplex Geometry.
Rocky Mountain Journal of Mathematics,
Vol. 26,
Issue. 1,
2002.
Vol. 1,
Issue. ,
p.
453.
2002.
Vol. 1,
Issue. ,
p.
665.
2002.
Vol. 1,
Issue. ,
p.
239.

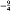 and −1 strictly.
and −1 strictly.