Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-05-16T22:33:46.770Z Has data issue: false hasContentIssue false
  • English
  • Français

Global rigidity of higher rank lattice actions with dominated splitting

Part of: Smooth dynamical systems: general theory Lie groups

Published online by Cambridge University Press:  27 April 2023

HOMIN LEE Open the ORCID record for HOMIN LEE [Opens in a new window]
HOMIN LEE*
Affiliation:
Department of Mathematics, Northwestern University, Evanston 60208, IL, USA
*
e-mail: homin.lee@northwestern.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 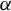$\alpha $ be a 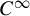$C^{\infty }$ volume-preserving action on a closed n-manifold M by a lattice 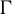$\Gamma $ in 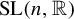$\mathrm {SL}(n,\mathbb {R})$, 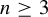$n\ge 3$. Assume that there is an element 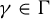$\gamma \in \Gamma $ such that 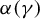$\alpha (\gamma )$ admits a dominated splitting. We prove that the manifold M is diffeomorphic to the torus 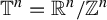${{\mathbb T}^{n}={\mathbb R}^{n}/{\mathbb Z}^{n}}$ and 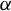$\alpha $ is smoothly conjugate to an affine action. Anosov diffeomorphisms and partial hyperbolic diffeomorphisms admit a dominated splitting. We obtained a topological global rigidity when 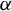$\alpha $ is 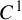$C^{1}$. We also prove similar theorems for actions on 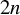$2n$-manifolds by lattices in $\textrm {Sp}(2n,{\mathbb R})$ with 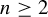$n\ge 2$ and 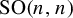$\mathrm {SO}(n,n)$ with 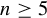$n\ge 5$.

Keywords

rigidityZimmer programgroup action

MSC classification

Primary: 37C85: Dynamics of group actions other than ${bf Z}$ and ${bf R}$, and foliations
Secondary: 22E40: Discrete subgroups of Lie groups
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 3 , March 2024 , pp. 799 - 828
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brown, A., Fisher, D. and Hurtado, S.. Zimmer’s conjecture: subexponential growth, measure rigidity, and strong property $(\textsf{T})$ . Ann. of Math. (2) 196 (2022), 891–940.CrossRefGoogle Scholar
Brown, A., Fisher, D. and Hurtado, S.. Zimmer’s conjecture for actions of $\textrm{SL}(m,\mathbb{Z})$ . Invent. Math. 221(3) (2020), 1001–1060.CrossRefGoogle Scholar
Brown, A., Fisher, D. and Hurtado, S.. Zimmer’s conjecture for non-uniform lattices and escape of mass. Preprint, 2022, arXiv:2105.14541.Google Scholar
Bieberbach, L.. Über die Bewegungsgruppen der Euklidischen Räume. Math. Ann. 70(3) (1911), 297–336.Google Scholar
Bieberbach, L.. Über die Bewegungsgruppen der Euklidischen Räume (Zweite Abhandlung.) Die Gruppen mit einem endlichen Fundamentalbereich. Math. Ann. 72(3) (1912), 400–412.CrossRefGoogle Scholar
Brin, M. and Manning, A.. Anosov diffeomorphisms with pinched spectrum. Dynamical Systems and Turbulence, Warwick 1980 (Coventry, 1979/1980) (Lecture Notes in Mathematics, 898). Eds. D. A. Rand and L.-S. Young. Springer, Berlin, 1981, pp. 48–53.Google Scholar
Borel, A.. Density properties for certain subgroups of semi-simple groups without compact components. Ann. of Math. (2) 72 (1960), 179–188.Google Scholar
Brown, A., Hertz, F. R. and Wang, Z.. Global smooth and topological rigidity of hyperbolic lattice actions. Ann. of Math. (2) 186(3) (2017), 913–972.CrossRefGoogle Scholar
Feres, R.. Actions of discrete linear groups and Zimmer’s conjecture. J. Differential Geom. 42(3) (1995), 554–576.Google Scholar
Fulton, W. and Harris, J., Representation Theory: A First Course (Readings in Mathematics, Graduate Texts in Mathematics, 129). Springer-Verlag, New York, 1991.Google Scholar
Fisher, D.. Groups acting on manifolds: around the Zimmer program. Geometry, Rigidity, and Group Actions (Chicago Lectures in Mathematics). Eds. B. Farb and D. Fisher. University of Chicago Press, Chicago, IL, 2011, pp. 72–157.Google Scholar
Fisher, D., Kalinin, B. and Spatzier, R.. Global rigidity of higher rank Anosov actions on tori and nilmanifolds. J. Amer. Math. Soc. 26(1) (2013), 167–198. With an appendix by J. F. Davis.CrossRefGoogle Scholar
Feres, R. and Labourie, F.. Topological superrigidity and Anosov actions of lattices. Ann. Sci. Éc. Norm. Supér. (4) 31(5) (1998), 599–629.Google Scholar
Fisher, D., Morris, D. W. and Whyte, K.. Nonergodic actions, cocycles and superrigidity. New York J. Math. 10 (2004), 249–269.Google Scholar
Franks, J.. Anosov diffeomorphisms. Global Analysis (Berkeley, CA, 1968) (Proceedings of Symposia in Pure Mathematics, Vol. XIV) . Eds. S. S. Chern and S. Smale. American Mathematical Society, Providence, RI, 1970, pp. 61–93.Google Scholar
Gorodnik, A.. Open problems in dynamics and related fields. J. Mod. Dyn. 1(1) (2007), 1–35.CrossRefGoogle Scholar
Goetze, E. R. and Spatzier, R. J.. Smooth classification of Cartan actions of higher rank semisimple Lie groups and their lattices. Ann. of Math. (2) 150(3) (1999), 743–773.CrossRefGoogle Scholar
Hiraide, K.. A simple proof of the Franks–Newhouse theorem on codimension-one Anosov diffeomorphisms. Ergod. Th. & Dynam. Sys. 21(3) (2001), 801–806.Google Scholar
Jacobson, N.. Basic Algebra I, 2nd edn. W. H. Freeman and Company, New York, 1985.Google Scholar
Katok, A. and Lewis, J.. Global rigidity results for lattice actions on tori and new examples of volume-preserving actions. Israel J. Math. 93 (1996), 253–280.Google Scholar
Katok, A., Lewis, J. and Zimmer, R.. Cocycle superrigidity and rigidity for lattice actions on tori. Topology 35(1) (1996), 27–38.Google Scholar
Margulis, G. A. and Qian, N.. Rigidity of weakly hyperbolic actions of higher real rank semisimple Lie groups and their lattices. Ergod. Th. & Dynam. Sys. 21(1) (2001), 121–164.Google Scholar
Newhouse, S. E.. On codimension one Anosov diffeomorphisms. Amer. J. Math. 92 (1970), 761–770.Google Scholar
Pesin, Y. B.. Lectures on Partial Hyperbolicity and Stable Ergodicity (Zurich Lectures in Advanced Mathematics). European Mathematical Society, Zürich, 2004.Google Scholar
Prasad, G. and Rapinchuk, A. S.. Irreducible tori in semisimple groups. Int. Math. Res. Not. IMRN 2001(23) (2001), 1229–1242.Google Scholar
Hertz, F. R. and Wang, Z.. Global rigidity of higher rank abelian Anosov algebraic actions. Invent. Math. 198(1) (2014), 165–209.CrossRefGoogle Scholar
Rudolph, G. and Schmidt, M.. Differential Geometry and Mathematical Physics. Part I. Manifolds, Lie Groups and Hamiltonian Systems (Theoretical and Mathematical Physics). Springer, Dordrecht, 2013.Google Scholar
Zimmer, R. J.. Ergodic Theory and Semisimple Groups (Monographs in Mathematics, 81). Birkhäuser Verlag, Basel, 1984.Google Scholar