No CrossRef data available.
Article contents
Grid method for divergence of averages
Part of:
Ergodic theory
Published online by Cambridge University Press: 11 April 2023
Abstract
In this paper, we will introduce the ‘grid method’ to prove that the extreme case of oscillation occurs for the averages obtained by sampling a flow along the sequence of times of the form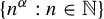 
$\{n^\alpha : n\in {\mathbb {N}}\}$, where 
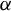$\alpha $ is a positive non-integer rational number. Such behavior of a sequence is known as the strong sweeping-out property. By using the same method, we will give an example of a general class of sequences which satisfy the strong sweeping-out property. This class of sequences may be useful to solve a long-standing open problem: for a given irrational 
$\alpha $, whether the sequence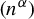 
$(n^\alpha )$ is bad for pointwise ergodic theorem in 
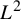$L^2$ or not. In the process of proving this result, we will also prove a continuous version of the Conze principle.
Keywords
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
Akcoglu, M., Bellow, A., Jones, R. L., Losert, V., Reinhold-Larsson, K. and Wierdl, M.. The strong sweeping out property for lacunary sequences, Riemann sums, convolution powers, and related matters. Ergod. Th. & Dynam. Sys. 16(2) (1996), 207–253.CrossRefGoogle Scholar
Bergelson, V., Boshernitzan, M. and Bourgain, J.. Some results on nonlinear recurrence. J. Anal. Math. 62 (1994), 29–46.CrossRefGoogle Scholar
Bellow, A.. On “bad universal” sequences in ergodic theory. II. Measure Theory and Its Applications (Sherbrooke, Quebec, 1982) (Lecture Notes in Mathematics, 1033). Eds. Belley, J.-M., Dubois, J. and Morales, P.. Springer, Berlin, 1983, pp. 74–78.CrossRefGoogle Scholar
Bellow, A.. Perturbation of a sequence. Adv. Math. 78(2) (1989), 131–139.10.1016/0001-8708(89)90030-3CrossRefGoogle Scholar
Besicovitch, A. S.. On the linear independence of fractional powers of integers. J. Lond. Math. Soc. (2) 15 (1940), 3–6.CrossRefGoogle Scholar
Bourgain, J.. On the maximal ergodic theorem for certain subsets of the integers. Israel J. Math. 61(1) (1988), 39–72.10.1007/BF02776301CrossRefGoogle Scholar
Buczolich, Z. and Mauldin, R. D.. Divergent square averages. Ann. of Math. (2) 171(3) (2010), 1479–1530.CrossRefGoogle Scholar
Boshernitzan, M., Kolesnik, G., Quas, A. and Wierdl, M.. Ergodic averaging sequences. J. Anal. Math. 95 (2005), 63–103.10.1007/BF02791497CrossRefGoogle Scholar
Bourgain, J.. Pointwise ergodic theorems for arithmetic sets. Publ. Math. Inst. Hautes Etudes Sci. 69 (1989), 5–45; with an appendix by the author, H. Furstenberg, Y. Katznelson and D. S. Ornstein.CrossRefGoogle Scholar
Buczolich, Z.. Universally
${L}^1$
good sequences with gaps tending to infinity. Acta Math. Hungar. 117(1–2) (2007), 91–140.10.1007/s10474-007-6068-8CrossRefGoogle Scholar
${L}^1$
good sequences with gaps tending to infinity. Acta Math. Hungar. 117(1–2) (2007), 91–140.10.1007/s10474-007-6068-8CrossRefGoogle ScholarCalderón, A.-P.. Ergodic theory and translation-invariant operators. Proc. Natl. Acad. Sci. USA 59 (1968), 349–353.CrossRefGoogle ScholarPubMed
Conze, J.-P.. Convergence des moyennes ergodiques pour des sous-suites. Contributions au calcul des probabilités (Mémoires de la Société Mathématique de France, 35). Bulletin de la Société Mathématique de France, France, 1973, pp. 7–15.Google Scholar
Jones, R. L.. Strong sweeping out for lacunary sequences. Chapel Hill Ergodic Theory Workshops (Contemporary Mathematics, 356). Ed. Assani, I.. American Mathematical Society, Providence, RI, 2004, pp. 137–144.10.1090/conm/356/06501CrossRefGoogle Scholar
del Junco, A. and Rosenblatt, J.. Counterexamples in ergodic theory and number theory. Math. Ann. 245(3) (1979), 185–197.CrossRefGoogle Scholar
Jones, R. L. and Wierdl, M.. Convergence and divergence of ergodic averages. Ergod. Th. & Dynam. Sys. 14(3) (1994), 515–535.10.1017/S0143385700008002CrossRefGoogle Scholar
Krengel, U.. On the individual ergodic theorem for subsequences. Ann. Math. Stat. 42 (1971), 1091–1095.CrossRefGoogle Scholar
LaVictoire, P.. Universally
${\mathrm{L}}^1$
-bad arithmetic sequences. J. Anal. Math. 113 (2011), 241–263.10.1007/s11854-011-0006-yCrossRefGoogle Scholar
${\mathrm{L}}^1$
-bad arithmetic sequences. J. Anal. Math. 113 (2011), 241–263.10.1007/s11854-011-0006-yCrossRefGoogle ScholarLind, D. A.. Locally compact measure preserving flows. Adv. Math. 15 (1975), 175–193.10.1016/0001-8708(75)90133-4CrossRefGoogle Scholar
Mirek, M.. Weak type (1, 1) inequalities for discrete rough maximal functions. J. Anal. Math. 127 (2015), 247–281.CrossRefGoogle Scholar
Parrish, A.. Pointwise convergence of ergodic averages in Orlicz spaces. Illinois J. Math. 55(1) (2011), 89–106.CrossRefGoogle Scholar
Reinhold-Larsson, K.. Discrepancy of behavior of perturbed sequences in
${L}^p$
spaces. Proc. Amer. Math. Soc. 120(3) (1994), 865–874.Google Scholar
${L}^p$
spaces. Proc. Amer. Math. Soc. 120(3) (1994), 865–874.Google ScholarRosenblatt, J. M. and Wierdl, M.. Pointwise ergodic theorems via harmonic analysis. Ergodic Theory and Its Connections with Harmonic Analysis (Alexandria, 1993) (London Mathematical Society Lecture Note series, 205). Cambridge University Press, Cambridge, 1995, 3–151.CrossRefGoogle Scholar
Trojan, B.. Weak type (1, 1) estimates for maximal functions along 1-regular sequences of integers. Studia Math. 261(1) (2021), 103–108.CrossRefGoogle Scholar
Urban, R. and Zienkiewicz, J.. Weak type (1, 1) estimates for a class of discrete rough maximal functions. Math. Res. Lett. 14(2) (2007), 227–237.CrossRefGoogle Scholar
Wierdl, M.. Pointwise ergodic theorem along the prime numbers. Israel J. Math. 64(3) (1988), 315–336.CrossRefGoogle Scholar