Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Boyle, Mike
Pavlov, Ronnie
and
Schraudner, Michael
2010.
Multidimensional sofic shifts without separation and their factors.
Transactions of the American Mathematical Society,
Vol. 362,
Issue. 9,
p.
4617.
Salo, Ville
and
Törmä, Ilkka
2012.
How the World Computes.
Vol. 7318,
Issue. ,
p.
636.
PAVLOV, RONNIE
2014.
A characterization of topologically completely positive entropy for shifts of finite type.
Ergodic Theory and Dynamical Systems,
Vol. 34,
Issue. 6,
p.
2054.
Barbieri, Sebastián
Gómez, Ricardo
Marcus, Brian
and
Taati, Siamak
2020.
Equivalence of relative Gibbs and relative equilibrium measures for actions of countable amenable groups.
Nonlinearity,
Vol. 33,
Issue. 5,
p.
2409.
Wibmer, Michael
2024.
Étale difference algebraic groups.
Annales de l'Institut Fourier,
Vol. 74,
Issue. 4,
p.
1451.

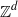 group shifts and Bernoulli factors
group shifts and Bernoulli factors