Article contents
Hölder shadowing on finite intervals
Published online by Cambridge University Press: 30 June 2014
Abstract
For any 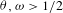 ${\it\theta},{\it\omega}>1/2$, we prove that, if any
${\it\theta},{\it\omega}>1/2$, we prove that, if any 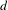 $d$-pseudotrajectory of length
$d$-pseudotrajectory of length 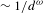 ${\sim}1/d^{{\it\omega}}$ of a diffeomorphism
${\sim}1/d^{{\it\omega}}$ of a diffeomorphism 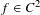 $f\in C^{2}$ can be
$f\in C^{2}$ can be 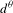 $d^{{\it\theta}}$-shadowed by an exact trajectory, then
$d^{{\it\theta}}$-shadowed by an exact trajectory, then 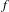 $f$ is structurally stable. Previously it was conjectured [S. M. Hammel et al. Do numerical orbits of chaotic dynamical processes represent true orbits. J. Complexity3 (1987), 136–145; S. M. Hammel et al. Numerical orbits of chaotic processes represent true orbits. Bull. Amer. Math. Soc.19 (1988), 465–469] that for
$f$ is structurally stable. Previously it was conjectured [S. M. Hammel et al. Do numerical orbits of chaotic dynamical processes represent true orbits. J. Complexity3 (1987), 136–145; S. M. Hammel et al. Numerical orbits of chaotic processes represent true orbits. Bull. Amer. Math. Soc.19 (1988), 465–469] that for 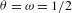 ${\it\theta}={\it\omega}=1/2$, this property holds for a wide class of non-uniformly hyperbolic diffeomorphisms. In the proof, we introduce the notion of a sublinear growth property for inhomogeneous linear equations and prove that it implies exponential dichotomy.
${\it\theta}={\it\omega}=1/2$, this property holds for a wide class of non-uniformly hyperbolic diffeomorphisms. In the proof, we introduce the notion of a sublinear growth property for inhomogeneous linear equations and prove that it implies exponential dichotomy.
Information
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2014
References
- 5
- Cited by

